Кеплер заңдарының математикалық тұжырымдалуы және астрономиялық маңызы

Пән: Физика
Жұмыс түрі: Реферат
Тегін: Антиплагиат
Көлемі: 3 бет
Таңдаулыға:

Кеплер заңдары

Кеплер Коперник ілімін жалғастырушы және дамытушы болды. Бастапқы кезде Кеплер ғаламшарларды шеңбер бойымен қозғалады деп есептеп, кейінірек ол пайымдауларынан бас тартып, ғаламшарлар қозғалысының келесі 3 заңын ашты:

1. Барлық ғаламшарлар эллипстер бойымен қозғалады және оның бір фокусында Күн тұрады;

2. Ғаламшарлардың радиус-векторлары тең уақыт аралықтарында теңдей аудандар сызады;

3. Ғаламшарлардың Күнді айналуының сидерлік периодтарының квадраттары олардың эллипстік орбиталарының үлкен жарты осьтерінің кубтарына пропорционал ( 2. 3-сурет ) .

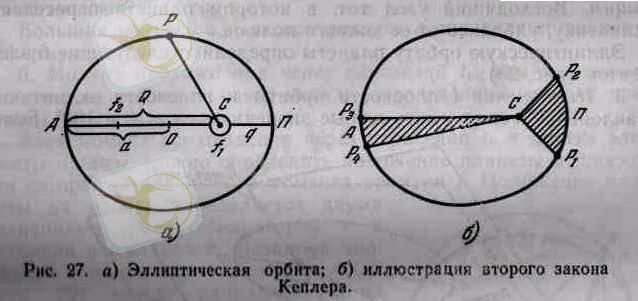
2. 3-сурет. а) Эллипстік орбита; б) Кеплердің екінші заңын түсіндіру

Мұндағы, f ₁ , f ₂ - фокустар, ол АП үлкен оське тең. АО қашықтығы үлкен жартылай ось деп аталады, О-эллипс центрі, Оf ₁ /OП=е - эллипс эксцентриситеті. Ғаламшарлар орбиталарының шеңберден айырмашылығы аз, сондықтан олардың эксцентриситеттері де аз шамаға тең.

Кеплердің 1- (жалпылама) заңы

Кеплер өз заңдарын эмпирикалық түрде, ғаламшарлардың көрінетін қозғалыстарын зерттеу нәтижесінде алды. Сондықтан жоғарғы келтірілген Кеплердің 1-ші заңы тек Күн жүйесінің үлкен ғаламшарлары мен Күнді айналып жүретін олардың денелері үшін дұрыс болады.

Егер аспан денелерінің қозғалысын жалпы түрде қарастырсақ, жоғарғы айтылған заңды келесі түрде тұжырымдау керек: тартылыс күші әсерінен бір дене екінші дененің тарту өрісінде қозғалады, бұл қозғалыс шеңбер, эллипс, парабола немесе гипербола түрінде болады. Бұл тұжырымдамада Кеплердің 1-ші заңы кометалар, үлкен ғаламшарлардың серіктері, қос жұлдыздар, т. б. аспан денелері үшін дұрыс болады.

Кеплердің 2-ші заңы

Тік бұрышты координаттар жүйесін қарастырайық. Координаттар басы тартылыс центрінде орналассын, ал ху жазықтығы дене орбитасының жазықтығымен сәйкес болсын. ( 2. 4-сурет )

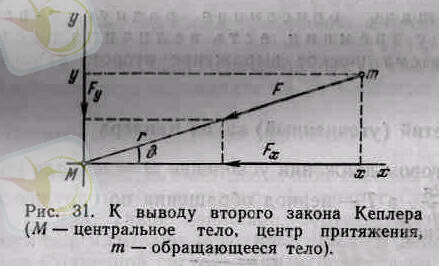
2. 4-сурет. Кеплердің екінші заңын қорытуды түсіндіру
( М - орталық дене, тартылыс центрі, m - айналатын дене)

Күш пен үдеудің х және у координат осьтеріне құраушыларын тауып, қозғалыс теңдеуін келесі түрде жазайық:

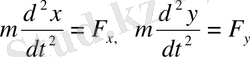(2. 1. 3)

Бұл теңдеулерді сәйкесінше у және х -ке көбейтіп және алғашқысынан соңғысын шегерсек, мынадай өрнекке келеміз:

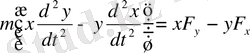(2. 1. 4)

немесе

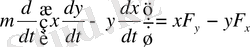(2. 1. 5)

Күш орталық болғандықтан :

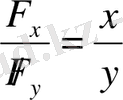, яғни . (2. 1. 6)

Олай болса,

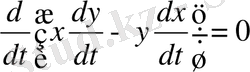(2. 1. 7) немесе

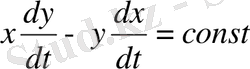. (2. 1. 8)

Полярлы координаттар арқылы өрнектесек:

, (2. 1. 9)

мұндағы r - нүктенің координата басынан қашықтығы (радиус-вектор), 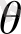- поляр бұрышы. Егер тік бұрышты координаттардан поляр координаттарына көшсек, онда жоғарыдағы өрнек:

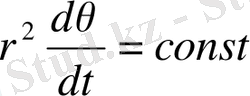(2. 1. 10)

түріне келеді.

Кеплердің үшінші (түзетілген) заңы

Дөңгелектік қозғалыс кезінде үдеу 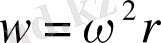, мұндағы бұрыштық жылдамдық 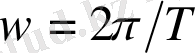, ал - айналу периоды болса, онда үдеу:

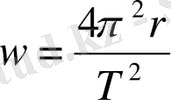(2. 1. 11)

түрінде анықталады Массасы m аспан денесінің массасы М орталық денені шеңбер бойымен айнала қозғалысын қарастырайық, олай болса жоғарыдағы өрнекке сәйкес салыстырмалы үдеу:

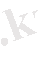
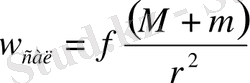-ге (2. 1. 12)

тең, 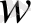және - екеуі бір шама, яғни үдеу болғандықтан, теңдеулердің оң жақтарын теңестіріп:

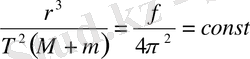(2. 1. 13)

өрнегін аламыз. Аспан денесінің қозғалысын эллипс бойымен қарастырсақ, сонда (2. 1. 13) өрнекке ұқсас өрнекті аламыз, бірақ мұнда шеңбер радиусы r үлкен жарты ось а -ға алмастырылады, ал Т дененің эллипс бойымен айналу периодын білдіреді. Осы өрнекті массалары m _ және m ₂ екі дене үшін жазайық, олардың эллипстік орбиталарының үлкен жарты осьтері а ₁ және а ₂ , ал айналу периодтарын Т ₁ және Т ₂ деп белгілесек, сонда:

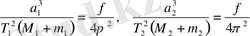(2. 1. 14)

Бұл Кеплердің 3-заңының түзетілген түрі. Егер екі ғаламшарның Күнді айнала қозғалысын қарастырсақ, яғни М ₁ =М ₂ болса және ғаламшарлар массасы Күн массасымен салыстырғанда ескермейтіндей аз болса ( 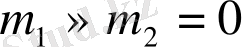), онда Кеплердің бақылаулар нәтижесінде алған:

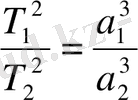(2. 1. 15)

өрнегіне келеміз. (2. 1. 13) және (2. 1. 14) өнектерінің астрономиядағы маңызы өте зор, өйткені олар аспан денелерінің массаларын аңықтауға мүмкіндік береді.

... жалғасы

Сіз бұл жұмысты біздің қосымшамыз арқылы толығымен тегін көре аласыз.