Көп өлшемді объектілердің фракталдық өлшемділіктері

Пән: Математика, Геометрия
Жұмыс түрі: Реферат
Тегін: Антиплагиат
Көлемі: 7 бет
Таңдаулыға:

Көп өлшемді объектілердің фракталдық өлшемділіктері

Бірөлшемді фракталды объектілер өзұқсастық немесе масштабтық инвариантты қасиетке ие: объектінің бөлігі толығына ұқсас. Егер анықтаушы айнымалылар саны бірден көп болса және осы айнымалылардың ұқсастық коэффициенті әр-түрлі болса, онда мұндай фракталды объектілерді өзаффинді деп аталады. Өзұқсас фракталға қарапайым мысалы ретінде біртекті ортада қозғалатын броуондық бөлшектің траекториясын келтіруге болады. Бұл жағдайда координаттық өстер өзара тең, ұқсастық коэффициенті барлық бағыттарда бірдей. Ал бөлшектің координатасының уақытқа тәуелділігі өзаффинді қисықпен сипатталады, себебі бөлшектің орын ауыстыруы уақытқа байланысты бейсызық түрде өзгереді және координата мен уақыттың ұқсастық коэффициенты әртүрлі. Күрделі генератордан шыққан сигналдардың формасы, жұқа қабыршақ шалаөткізгіштің кеңістіктік және уақыттық энергетикалық спектрлері, т. с. с. өзаффинді фракталдар болуы мүмкін.

Б. Мандельброт модельдік фракталдарға аффиндік көрсеткіштер енгізіп, сол арқылы фракталдық өлшемділіктер анықталатындығын, сонымен қатар олардың Херстің эмпирикалық көрсеткіштерімен ((4) тарау 3) мүмкін болатын байланыстарын көрсетті. Бірақ нақты жағдайларда сипаттамалық масштаб (аффиндік көрсеткіш) бір мәнді анықталмаған болып қалады. Эмпирикалық тұрақты арқылы периметр мен ауданның қатынасы, универсалды емес фракталдық өлшемділіктің тек бір ғана мәнін анықтайды. Фракталдану зандылықтарын білмей (2) Хаусдорф формуласын және басқа фракталдық өлшемділіктерді есептеу әдістерін өзаффинді объектілерге қолдануға болмайды.

Төменде өзаффинді объектілердің фракталдық өлшемділігін еркін параметрсіз анықтайтын әдісті және алынған нәтижелерді бейсызық генератордың хаосты сигналын сипаттауға қолдануды қарастырамыз.

Ұзындық L ( δ ), аудан F ( δ ), көлем V ( δ ) секілді фракталдық өлшемдер кез келген аддитивті M (массаның аналогы) физикалық шаманы анықтайтын жалпы формуламен табылады:

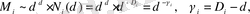
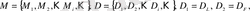(3)

мұндағы N ( δ ) - жиын элементтерін сипаттауға жеткілікті ұяшықтардың минимум саны.

Фракталдар үшін интегралдау нәтижесі интервалды бөлетін нүктелер санына байланысты D- ны M арқылы өрнектейтін кері есеп қоялық. δ өлшемді ұяшықтың нөмірін немесе δ- ның мәнін кездейсоқ таңдау арқылы, бұл әдіспен реттелген және кездейсоқ фракталдарды да қарастыруға болады.

Өлшеудің салыстырмалы масштабтарын енгізейік

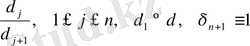. (4)

Фракталдық өлшемнің (3) жалпы формуласы бойынша

, ,

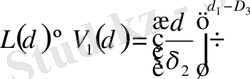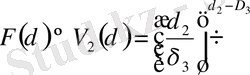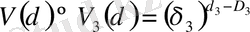, (5)

мұндағы d ₁ = 1, d ₂ = 2, d ₃ = 3 - ұзындықтың, ауданның, көлемнің топологиялық өлшемділіктері. (5) -формуладан δ ₂ және δ ₃ -ті алмастырсақ:

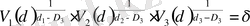. (6)

n -өлшемді болған жағыдайда

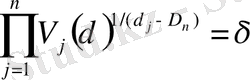(7)

мұндағы V _j ( δ ) - көпөлшемді фракталдық шама, D _n - оның фракталдық өлшемділігі. Егер фракталдық шамалар топологиялық өлшемділіктері d _i , i = 1, 2, 3 болатын сызықтың жазықтықтың, көлемнің деформациясынан пайда болатынын ескерсек, онда жалпы түрде

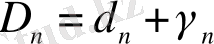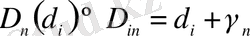, , , (8)

мұндағы γ _n -скейлинг көрсеткіші, яғни D _n - нің бөлшек бөлігі.

D _n -і анықтайтын (7) -өрнек, n -дәрежелі бейсызық теңдеу болып табылады. (7) -өрнектегі V _j көрсеткіштері бірдей, яғни:

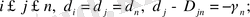
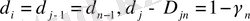(9)

болғанда γ _n -ге қатысты сызықты теңдеулер аламыз.

(9) - формуладағы шарт D _n өлшемділікті n -өлшемді объектінің топологиялық өлшемділіктері d _n және d _n- ₁ болатын элементтердің каскадты деформациясы арқылы құрылатындығын көрсетеді. Мысалы, d _n- ₁ арқылы фракталдану деп n = 1 болғандағы нүктелер жиынынан тұратын фракталдық қисық қарастырылады, n= 3 болғанда фракталдық объект қисықтардан құралған беттің деформациясынан түзіледі.

(7) және (9) екі шарт орындалғанда бірдей нәтиже шығады:

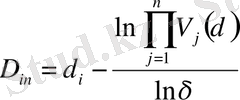. (10)

Егер (7) -теңдеудегі V, d, D мәндерін n бойынша орташа мәні деп қабылдасақ, онда D байланысты сызықты теңдеу аламыз:

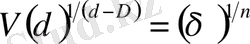, (11)

осыдан

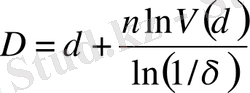. (12)

(10) -формуладан 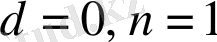жағдай үшін (2) формула шығады.

(9) шарттың орындалу мысалын қарастыралық. Айталық

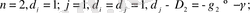
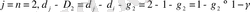. (13)

Бұл сызықтық деформациялану жолымен фракталдық бетті құру шарттарына сәйкес келеді.

Бұл жағдайда (7) теңдеу келесі түрге өзгереді

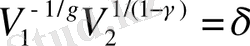. (14)

Осыдан шыққан γ қатысты квадрат теңдеуді шеше отырып фракталдық өлшемділікті табамыз:

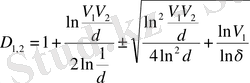, (15)

мұндағы минус таңбасы минимальды, локальды мәнді анықтайды. Бұл формулалар екі өлшемді объектінің әр түрлі өлшеу масштабындағы қасиеттерінің сапалық өзгерісін фракталдық өлшемділіктің өзгерісі арқылы сипаттайды.

(7) формуланы қолдану n топологиялық өлшемділігі бар δ өлшеу масштабына тәуелді 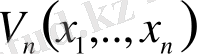объектінің фракталдық шамасын білуді қажет етеді. Бұл тәуелділікті аз δ интервалымен анықталатын x _n ( t ) секірмелі функцияның қосындысы арқылы іздеуге болады. Мысалы, L ( δ ) - фракталдық элементтің периметрі келесі өрнек ретінде қабылданады:

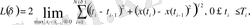(16)

мұндағы t айнымалы оның симметрия өсі бойымен бағытталған. Осыған сәйкес фракталдық аудан мынаған тең:

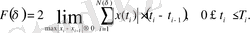(17)

(16), (17) формулалар функцияның өсімшесінің өзгерісін шектейтін Липшиц-Гельдер шарты орындалғанда қолданылады. Немесе эквивалентті шарт, модульдің үзіліссіздігі:

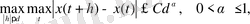(18)

мұндағы С -қандайда бір тұрақты шама. Мұндағы α Липшиц-Гельдер көрсеткіші шаманың өсімшесін сипаттайды және мағынасы бойынша фракталдық обьектінің өте қарапайым, өзұқсас құрылымды ұяшығының фракталдық өлшемділігімен байланысты. Өзұқсас объектілер үшін ұяшық пен жалпы объектінің фракталдық өлшемділігі α = D болады.

Жоғарыда келтірілген аргументтер x ( t ) бір мәнді функциямен сипатталатын өзаффинді фракталдардың өлшемділіктерін периметір мен көлемнің арақатынасы арқылы анықтауға мүмкіндік береді. x ( t ) функциясы көп айнымалы 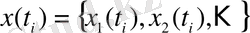болғанда, фракталды жиынды түрлендіру арқылы жай ұяшықтарды бөліп алатын геометриялық бейнені анықтау әдістерін қолдану кажет.

(16), (17) формулаларды кез-келген сипаттамалық масштабта объектілердің фракталдық шамасын анықтауда қолдануға болады. Оларды пайдалана отырып (15) формуладан 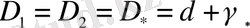болатын күрделі формадағы өзара бүтіндік фракталдардың өлшемділігін табамыз. Бұл жағдайда γ _* = S _* ( I ) = 0. 806 деп күтуге болады. Бірлік радиусты ( n + γ ) өлшемді сферадан тұратын ең қарапайым формалы фракталдар жағдайында γ _* = f _* ( I ) = 0. 567 болуы тиіс.

Радиусы R болатын n- өлшемді сфераның көлемі

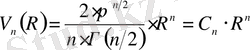, (19)

мұндағы, Г ( n/ 2) - гамма-функция. Фракталдың сипаттамалық масштабы болмайды деп ескеріп, R = 1 тең деп қабылдаймыз. Өлшемділігі n + γ бірлік радиусты шеңбердің көлемін келесі түрде жазамыз

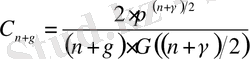, (20)

мұндағы γ - фракталдық өлшемділіктің бөлшек бөлігі. (19) формула фракталдық өлшемділігі ( n + γ ) болатын кеңістікте орналастырылған обьектінің тұрақты көлемін анықтайды. Өз максимум мәндеріне нормаланған тұрақты ( С _n+γ ) және фракталды ( С _n ( γ ) ) көлемдердің қосындысы бірге тең:

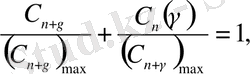
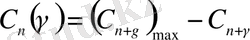(21)

( С _n+γ ) _max мәні, (19) өрнекте n + γ = 5 болғанда ( n + γ ) бойынша туындысы, нөлге тең болады. Осыларды ескеріп D _n -ді γ арқылы анықтау үшін С _n ( γ ) қолданамыз.

Өзаффинді сигналдарды сипаттау

Алынған нәтижелерді қолдану мүмкіндігін көрсету үшін Вейерштрасс-Мандельброттың өзаффинді фракталдық қисықтарын b , A параметрлерінің әртүрлі мәндері үшін қарастырайық:

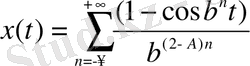. (22)

Ұзындығы L ( δ ) қисықпен шектелген F ( δ ) фракталдық ауданды бөліп алу схемасы 3-суретте көрсетілген. Жаңа 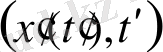тікбұрышты координат жүйесі, x ( t ) мен 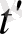өсінің қыйылысуы әр-түрлі күрделі құрылымдары бөліп алатындай етіп таңдалған. Екі қатар тұрған нөлдер интервалда 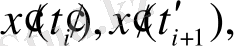яғни 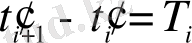, өсіне симметриялы қыйсық тұрғызайық. Бұл процедура, мәндер өсі бойынша түзу сызық болмайтын, 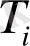параметрімен сипатталатын тұйықталған фракталдық қисықты алуға мүмкіндік береді. Осындай әр-түрлі мәндері бар фракталдық элементтерді бөле отырып фракталдық өлшемділіктің асимптотикалық мәндерін іздестіруге болады. Басқа жағдайларда T -ға тәуелді фракталдық өлшемділік туралы ғана айтуға болады. 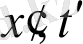айнымалыларды 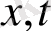ретінде қайта белгілеу арқылы (16), (17) формуланы қолданамыз. 4-суретте (15-17), (22) формулалармен табылған D ₁ және D ₂ мәндері көрсетілген. Вейерштрасс-Мандельброт өзіндік аффинді қисығы әртүрлі фракталдық өлшемділіктерге ие. Өзұқсастық ( D ₁ және D ₂ мәндерінің тепе-теңдігі) А параметрінің үлкен мәнінде 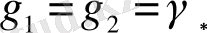, γ _* = S _* ( I ) = 0. 806 ғана бола алады. Екінші өзіндік ұқсастылық критерийі γ _* = f _* ( I ) = 0. 567 мұнда байқалмайды, себебі бұл қисықтар үшін 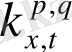мәні жоғары.

4-сурет. Фракталдық өлшемділіктің (22) формуладағы А параметіріне тәуелділігі. ( b = 1, 5) . - D ₁ , - D ₂

D ₁ , ₂

1. 806

T _i

3-сурет. Өзаффинді Вейерштрасс-Мандельброт қыйсығы.

b = 1. 5, A = 1. 8

1, 2

1, 4

1, 6

1, 8

2, 2

Мысал ретінде реалды физикалық процестің фракталды қисықтарын қарастырайық. 5 а -суретте параметрлері флуктуацияланатын автотербелмелі жүйенің теңдеуінен алынған, ұзақтығы бірдей сигналдар үшін 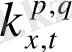мәнінің уақыт өсімен қиылысу санына ( ν ) тәуелділік қисығы көрсетілген

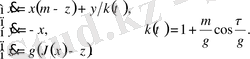(23)

Сигналдың формасы және соған орай фазалық суреті 5 б , 5 в суреттерінде көсетілген.

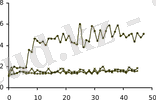
6-суретте параметрлері флуктуациялы генератор сигналдарының (15) формула бойынша есептелген фракталдық өлшемділіктері көрсетілген.

(23) теңдеулер жүйесі 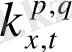мәні үлкен және әуейі, хаосты аттракторлы режимдегі параметрлерінің флуктуациясы бар автотербелмелі жүйені сипаттайды. Параметрлер флуктуациясын ескеру күрделі құрылымды сигналдарды ( g > 1) алуға және импульстердің масштабты инвариантты (фракталды) қасиеттерін бақылауға мүмкіндік береді. Фракталдық заңдылықтарды, яғни зерттеуде сигналдардың ішкі құрылымын ескермесек, біз сигналдың заңдылығын білу үшін стационар емес көп уақытқа тәуелді жағдайды қарастыруымыз қажет.

(15) өрнек өзаффинді, өзұқсас D _* ₁ және D _* ₂ екі кризистік фракталды өлшемділікті анықтайтындығы 6 суреттен көрінеді. Жоғарғы дәлдікте ( δ<δ _* ₁ ) D _* ₁ ≠ D _* ₂ қисықтың өзаффинділігі байқалады. Жазықтықтың өзаффинділігі керісінше, өлшеудің сызықтық масштабы үлкен ( δ>δ _* ₂ ) болғанда байқалады.