Паккард-Таккенс әдісімен күн магнит өрісінің уақыттық тізбегінің аттракторлық құрылымы мен корреляциялық өлшемділігін зерттеу


Күн белсенділігін Паккард-Таккенс әдісімен зерттеу нәтижелері
Күрделі жүйе сипаттамасы сынақтық түрде белгілі бір уақыт интервалында «маңызды» айнмалыны бақылау арқылы шектеледі. Кейде жалғыз айнымалы бойынша уақыттық тізбек аз ғана ақпарат беретін сияқты. Көбіне, жүйедегі «бір өлшемді» көзқарас беретін жайытқа қарсы келуге болар еді, шын мәнінде ол өзәра байланысқан көп айнымалылардан тұрады. Бұл қосымшада [2] уақыт тізбегі айтарлықтай көп ақпараттан тұратындығы көрсетіледі, ол жүйе динамикасының сиппаттамасында басқа айналмалылардың барлық тізбегін тасымалдайды және үлгісіз тәсілмен сәйкес жүйенің кейбір негізгі ерекшеліктерін идентификациялауға мүмкіндік береді.
Х 0 (t) -сынақтың өлшенген көлемінің бір тізбегі болсын. әрине, шын мәнінде, динамикалық процесте басқа айнымалылар да қатысуы керек. Алайда, біз ешбір нақты үлгіге сүйенбегендіктен, біз осы динамиканы өзімізге мәлім Х 0 (t) айнымалысы көмегімен қалыпқа келтіргіміз келеді. Осы мақсатпен {Х k (t) }, k=1, . . . n-1 айнымалысымен пайда болған фазалық кеңістікті қарастырайық. Біз білетіндей, бұл кеңістіктегі жүйенің кейбір мезгілдік күйі, мысалы, p нүктесіне сәйкес келеді, ал жүйе уақытта өтетін мұндай күйлер тізбегі, белгілі бір қисықты - фазалық траекторияны анықтайды. Уақыт өтісімен жүйеде белгілі бір тұрақтылық орнайды. Бірақ оның динамикасы диссипативті процестерді сипаттайтын детерминантты процедуралар жүйесіне келтірілуі керек. Бұл фазалық траекторяның жиынтығының фазалық кеңістіктің ішкі жиынына сәйкестігінде көрніс табады. Осы инвариантты ішкі жиын аттрактор деп аталады.
Бірінші қадам фазалық кеңістікті құрайтын айнымалылардың терімін анықтаудан тұады. Бұл үшін алғашқы уақыт бірлігін Х 0 (t) шамасы ретінде анықтаған, тізбектегі өспелі қозғалыстар терімі кей Фиксирленген кедергіге τ (τ = mΔt, мұнда m бүтін және Δt тізбектегі таңдамалар аралығындағы интервал) қысқа тізімге алмастырғн ыңғайлы. Сонымен бірге, сынақтық мәліметтер терімінен N эквидистантты нүктелерді таңдай келе, біз келесі дискретті айналмалы теріміне келеміз:
Х 0 : Х 0 (t 1 ), . . . , Х (t n )
Х 1 : Х 0 (t 1 + τ), . . . , Х (t n + τ)
.
.
.
. .
.
Х n-1 : Х 0 (t 1 + (n - 1) τ, …. ., Х (t n + (n-1) τ)
Қажетті τ-ды таңауда, бұл айнмалылардың сызықты тәуелді айнмалы екендігін күтуге болады, ал бұл болса фазаық кеңістікті анықтауға ең қажеттісі болып табылады және бұл айнымалыларды Х 0 (t) қатысты, сынақтан анықтлған жалғыз уақыт тізбегінен анықтауға болады. Осылайша, біз қолымыздағы бар ақпарат алғашқы уақыт тізбегіненнің бірөлшемді кеңістігі шегінен шығатын жүйе динамикасын көпөлшемді фазалық кеңістікте ала алатындығымыз көрінеді. Бұл ақпарат жүйесінің фазалық портретін, дәлірек айытсақ, ондан толық фазалық кеңістікті азөлшемді ішкі кеңістікке проекциясын салуға мүмкіндік береді.
Келесі векторлық белгілеулерді енгізейік: Х i - {Х 0 (t 1 ) . . . , Х 0 (t 1 + (n - 1) τ} координаттар мен фазалық кеңістіктер нүктесін білдірсін делік. осылайша барлық мәліметтер үшін Х i санау бастамасы белгіленеді және осы нүктеден қалған N-1 нүктеге дейінгі қашықтықты Х i - Xj есептенуге болады. Бұл Х i дан белгілі бір τ мөлшерінен аспайтын қашықтыққа артта қалатын, фазалық кеңістіктегі нүктелер санын септеуге мүмкіндік береді. Бұл процестерді бірлікі мәндер үшін қайталай келе, келесі өлшемді есептеуге болады:
C(ε) =
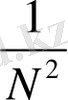
, (2. 28)
Мұндағы θ - Хевисайд функциясы: X<0 болғанда θ(x) = 0 және X>0 болса θ(x) = 1. C(ε) -нің нөлден ауытқуы Х i нүктесінің басқа нүктелер күтетіне әсері болып табылады. Сондықтан C(ε) функциясын аттрактордың интегралды корреляциялық функциясы ретінде қарастыруға болады.
Аз өлшемді ε ні алып, оны аттрактор құрлымын шекаралу үшін өзіндік өлшем ретінде пайдаланамыз. Егер ең соңғысы сызық болса, онда, берілген нүктге дейінгі қашықтық r -ден аспайтын сынақтық нүктелер саны r ∕ ε -ге пропорциональды болуы керек. Ал егер аттрактор жазықтық болса, онда мұндай нүктелер саны (r ∕ ε) -ға пропорционал болуы керек. Сондықтан салыстырмалы ε аз өлшемде C(ε) функциясы
C(ε) = ε d (2. 29)
сияқты өзгереді деп күтуге болады. Басқаша айытқанда, d аттрактор өлшемі lnC(ε) белгілі ε диапозонындағы lnε тәуелділікгімен беріледі
ln C(ε) = d lnε (2. 30)
Бұл нәтижелерден келесі алгоритм шығады:
1. Берілген уақыт тізбегінен n фазалық кеңістіктің өлешемдерінің өспелі мәндерін бірізді қарастыра келе, (2. 13) корреляциялық функция тұрғызу
2. (2. 15) -ке сәйкес, координаттар бсына жақын d ылдиын алу және бұл нәтиже n өскенде қалай өзгеретінін қарау.
3. Егер d мөлшері n-ге байланысты, қатынасты кішкентай n бір үстірт жоғары қойса, онда берілген уақыт тізбегіндегі жүйенің аттракторы болуы керек. Қанықтыуға шыққан d мөлшерін уақыт бірізділігімен келтірілген, оны аттрактор бірқалыптылығы ретінде қарастыруға болады. Жоғарыда айтылғандай, қанығыу бйқалатын n өлшемі берілген аттракторға сәйкес, сипаттаманы үлгілеуге қажетті айнымалылардың минималды саны болып табылады. d=n жағыдайда аттроктор көмегімен d және n қарастырылып отырған сигнал гаусстық ақ шуылға сәйкес келеді. Бұл климат динамикасы мен шуыл сигналы арасындағы нақты айырмашылықты белгілейді. Аттрактордың бірқалыптылығы бүтін емес санмен берілетіндігінен, бұл факт климаттық жүйенің өзгерісі мен өзгермелілігін түсінуге негіз болады, өйткені бұл ерекшеліктердің екеуі де хаостық динамиканың негізгі қасиеттерінежатады. Бұл динамика негізгі айнымалылардың шектелген теріміне келтіру фактісін айта кету керек, алайда бұл кезеңде олардың нақты табиғатын анықтау мүмкін емес.
Жоғарыдағы суреттелген әдіс жүйенің түрлі формадағы сәйкес электроэнцефалография мәліметтерін таңдауға да қолданылады. Мұнда терең ұйқы кезінде аттрактордың болатындығын айтуға болады. Субъектға байланысты, аттрактордың бір қалыптылығы 4 пен 4, 3 аралығында болады. Екінші жағынан, патологиялық белсенділіктің (элиппис сияқты) нақты кезеңдерінде бірқалыптылық өте аз, 2-ге жақын. Бұл нәтиже табиғатта кездесетін, мысалы, ауа райының тез арада өзгеруі және экономикалық шығармашылық сияқты күрделі жүйелерде талданады.
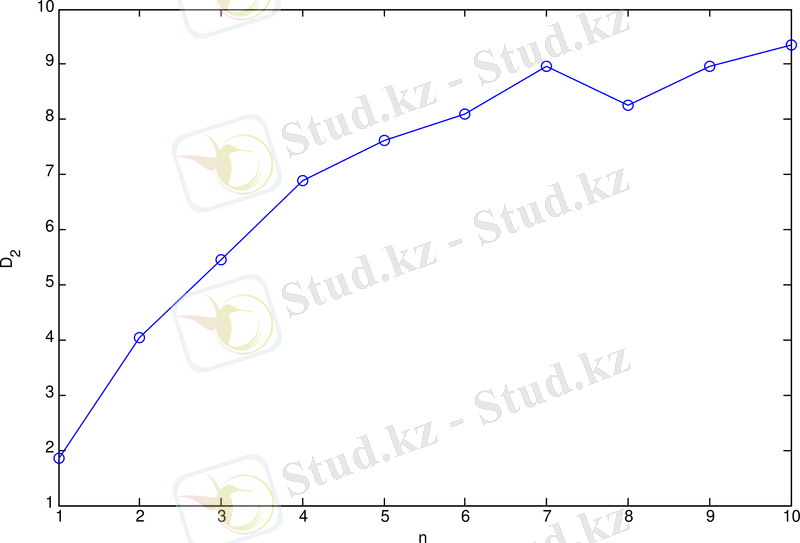
Орташа күн магнит өрісінің уақыттағы өзгерісі 2 тарауда көрсетілген уақыттық тізбегі бойынша күрделі жүйелер динамикасын айқындаудың Паккард - Таккенс әдісімен зерттелген. Бұл зерттеудің нәтижелері 3. 4-3. 17 суреттерде көрсетілген. Мұнда күн белсенділігінің максимумдары мен минимумдарының периодтары үшін D 2 өлшемінің фазалық айнмалылар саны n - ге тәуелділігі көрсетілген.
Бұл суреттерден мынаны көруге болады. КБ максимумдарының барлық периодтары үшін аттрактордың интегралдық корреляциялық функциясының ұяшық өлшеміне тәуелділігінде ұзындығы айтарлықтай түзу сызықты бөлігі бар және D 2 корреляциялық өлшемділігінің n-ге (фазылық айнымалылар санына) тәуелділігі n-нің 7 - 8 мәндерінде үстіртке шығады (қанығады) .
Бұл зерттеліп отырған уақыттық қатармен көрсетілген жүйеде аттрактор бар екенін, яғни оның динамикасы өте күрделі болса да детерминді екенін, және де жүйенің динамикасын айнымалылардың шектелген санымен сипаттауға болатынын көрсетеді. Сонымен қатар, үстірт D 2 -ң бүтін емес және 2-ден жоғары, ~7. 8 - 9. 8 мәндерінде бақыланады, яғни сәйкесінше аттрактор өлшемі бүтін емес.
3. 6 сурет - 1979-1982 жж аралығындағы КБ максимумы үшін орташа Күн магнит өрісінің уақыттағы өзгерісі аттракторының интегралдық корреляциялық функциясының ұяшық өлшеміне тәуелділігі
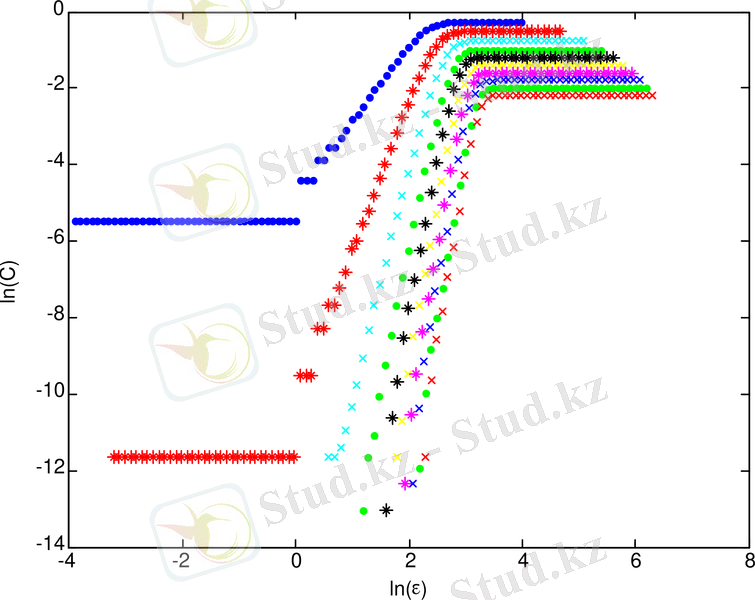
3. 7 сурет - 1979-1982 жж аралығындағы КБ максимумы үшін орташа Күн магнит өрісінің уақыттағы өзгерісі аттракторының жалпылама фракталдық өлшемділігінің фазалық айнымалылар санына тәуелділігі
3. 8 сурет - 1989-1992 жж аралығындағы КБ максимумы үшін орташа Күн магнит өрісінің уақыттағы өзгерісі аттракторының интегралдық корреляциялық функциясының ұяшық өлшеміне тәуелділігі
... жалғасы- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz