КҮРДЕЛІ СИГНАЛДАРДЫ ТАЛДАУДЫҢ ЖАҢА ӘДІСТЕРІ

Пән: Автоматтандыру, Техника
Жұмыс түрі: Материал
Тегін: Антиплагиат
Көлемі: 4 бет
Таңдаулыға:

КҮРДЕЛІ СИГНАЛДАРДЫ ТАЛДАУДЫҢ ЖАҢА ӘДІСТЕРІ

2. 1 Информациялық энтропия туралы түсінік Информациялық энтропия сөзіндегі «Информация» ұғымы әртүрлі мағынаға ие. Қоғамдық - саяси информация әлеуметтік жүйенің өзекті жаңалықтары туралы мәліметтердің жиыны болып табылады. Кибернетикада информация ұғымы сигналдарды сақтау, өңдеу және жіберумен байланысты. Ықтималдықтар теориясында информация аддитивті мөлшерлік өлшем ретінде кездейсоқ оқиғаларды бір-біріне қатысты ықтималдылығымен салыстыру арқылы енгізіледі. Барлық информация теориясы негізінде информацияны мөлшерлі бағалау жатыр. Қарапайым комбинаторикалық формада бұл тұжырымды Р. Хартли ұсынды, ал толық аяқталған түрін К. Шеннон тұжырымдады. Шеннон информация теориясы О және L екі таңбаның арасындағы (биттер арасындағы) қарапайым альтернативті таңдаудан шығады, ондағы L 1-ге, “иә”, “шындық” т. с. с. теңестірілсе, ал О 0-ге, “жоқ”, “жалған” теңестіріледі. Мұндай таңдау екі белгіден тұратын хабарды қабылдауға сәйкес келеді. Мұндай хабарда болатын информация мөлшері бірлік ретінде қабылданады және ол бит деп аталады. Сондықтан бит - екілік белгі және информация мөлшерінің өлшем бірлігі, ол екі байланысқан тең ықтималдықты таңдамадағы информация мөлшері ретінде анықталады. Айталық

(2. 1)

- Х және Y әріптерімен сәйкес белгіленген жүйенің күйін сипаттайтын айнымалылар жыйыны болсын. Егер 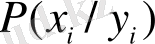- Х жүйесі 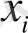күйде болғанда Y у _i күйіне өту ықтималдығы (шартты ықтималдық) болса, онда Y жүйесінің алған информациясы мынаған тең:

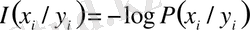. (2. 2)

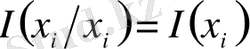- X жүйесіндегі 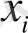оқиғасына қатысты 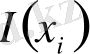информация мөлшері деп аталады.

Ықтималдық 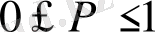арасында жатқандықтан I әрқашан оң шама.

Логарифм негізін таңдауға байланысты информация мөлшері екілік, ондық және натурал логарифм бойынша: сәйкесінше бит, дит, нат - пен өлшенеді.

Статистикалық физикада энтропия ∆Г - жүйенің ішкі макроскопиялық күйінің статистикалық салмағының логарифмі ретінде енгізіледі:

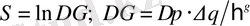, (2. 3)

мұндағы ∆p⋅∆q- фазалық көлем, ћ -Планк тұрақтысы, g -жүйенің еркіндік дәрежесінің саны. Классикалық физикада ћ қолданбайтындықтан энтропияны нақты анықтауға болмайды. (5) -ші формуланың түрі күрделі жүйенің энтропиясының аддитивтік талаптарынан шығады:

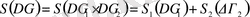(2. 4)

Идеал газдың энтропиясын (2. 3) -ші формула бойынша есептей отырып (2. 4) -ші формулаға келуге болады, мұндағы ∆Γ - идеал газдың қысымы, көлемі, температурасы бойынша анықталады.

Энтропия түсінігі сонымен қатар кездейсоқ шамалардың ықтималдықтарының таралуына да байланысты. Е _i энергияның теңықтималдықты таралуы кезінде жүйенің ішкі таралу ықтималдылығы былай анықталады.

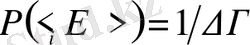Энтропияны мына түрде табамыз

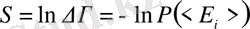(2. 5)

Орташа ықтималдықтың мағынасы бойынша (2. 5) былай жазылады:

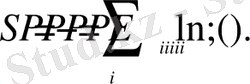(2. 6)

(2. 6) - бойынша анықталған энтропия информациялық энтропия деп аталады. (2. 2) және (2. 6) өрнектерін салыстыру арқылы информациялық энтропия информацияның орташа ықтималдық мәнін анықтайтындығы көрінеді. Жүйенің теңықтималды таралуы кезінде жүйе туралы анықталмағандық максимумге жетеді, яғни жүйе туралы барлық информация жоғалып энтропияға айналады (2. 5) . Тепе-тең жүйе информацияны сақтай алмайды. Информацияны білу анықталмағандықты азайтады. Сондықтан информация мөлшерін жоғалған анықталмағандық, яғни энтропия мөлшерімен өлшеуге болады:

I = S _pr - S _ps , (2. 7)

мұнда pr - индекс «априорлы» дегенді білдіреді (тәжірибеге дейін) ps «апостериорлы» (тәжірибеден кейін) . Осы себептен әдебиеттерде (2. 6) -ші өрнекпен анықталатын шама кейде информация деп аталады( егер ол қабылданса), кейде энтропия деп аталады (егер ол жоғалса) . Осылайша Х шамасы туралы информация Ү берілген кезде мына теңдікпен анықталады.

I ( X ) = S ( X ) - S ( X/Y ) . (2. 8)

(2. 6) -ші өрнектен энтропияның қасиеттері шығады:

алдын-ала белгілі хабардың энтропиясы 0 -ге тең.
барлық басқа жағдайлардаS >0 болады.

2. 2 Фракталдар мен мультифракталдар

Фракталдар және мультифракталдар теориясы қазір әртүрлі құбылыстарды түсіндіру үшін кең қолданады. Фракталдар санына мына обьектілер кіреді қатты кесілген формадағы сызықтар, беттер, денелер және олар кең масштабта қандай да бір қайталанушылыққа ие болады. Қайталану толық болуы мүмкін яғни толық ұқсас болады. ол Регулярлы фракталдар деп аталады. Ал кейде кездейсоқ болады оларды кездейсоқ фракталдар деп аталады. Фрактал дегеніміз - геометриялық обьект сызықтар, жазықтықтар, қатты бөлшектенген формадағы кеңістік денелері және олардың өзіне тән қасиеттері бар.

Табиғи фракталдардың қасиеттері тек l _min ≤ l ≤ l max қатынасын қанағаттандыратын l масштабында ғана қарастырылады, .

Бұл шектеулер табиғи, өйткені біз мысал ретінде - бөлшектенген Броундық бөлшектің тегіс емес траекториясын келтірген кезде, бұл бейненің ашық идеализация екенін түсінеміз. Оның мәнісі мынада кішкентай масштабта массаның ақырғылығы мен Броундық бөлшектің өлшемі және де әсерлесу уақытының ақырғылығы деп айтылады. Осы жайттарды ескерсек Броундық бөлшектің траекториясы қисық болып шығатынын көреміз.

... жалғасы

Сіз бұл жұмысты біздің қосымшамыз арқылы толығымен тегін көре аласыз.