Детерминдік жүйелердегі хаосты бағалау: Ляпунов көрсеткіштерін есептеу әдістері


Детерминдік жүйелердегі хаос қозғалыстың бастапқы шарттардан сезімтал тәуелді екенін білдіреді. Яғни, фазалық кеңістікте алғашқы уақытта бір біріне жақын екі траектория аз уақыттың ішінде экспоненциалды ажырайды. Егер d 0 - берілген екі нүктенің арасындағы бастапқы ара қашықтықтың өлшемі болса, онда t аз уақыт ішінде осы нүктелерден шыққан траекториялар арасындағы ара қашықтық мынаған тең болады:
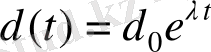 . (11)
. (11)
Егер жүйе айырымды теңдеулермен, немесе бейнелеумен сипатталса, онда
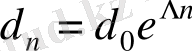 . (12)
. (12)
λ және Λ өлшемдері Ляпунов көрсеткіштері деп аталады.
Хаостық траекторияның экспоненциалды ажырауы аз аумақта ғана болуы мүмкін, өйткені егер жүйе шектелген болса (ал, көпшілік физикалық тәжірибелер шектелген жүйені сипаттайды), онда d ( t ) шексіз өсе бере алмайды. Сондықтан траекторияның ажырау мөлшерін анықтау үшін 13-суретте көрсетілгендей траектория бойындағы көптеген нүктелер бойынша экспоненциалды өсуін орташалау керек. Ляпунов көрсеткішін есептеу реперлі траекторияны (немесе тірек траектория) және көрші траекторияның нүктесін таңдап, d ( t ) / d 0 шамасын есептеуден басталады. d ( t ) ара қашықтығы тым үлкен болса (яғни экспоненциалды түрден оның өсі ауытқыса), зерттеуші жаңа «көрші» траекторияны тауып, қайтадан бастапқы d 0 ( t ) ара қашықтығын анықтайды. Ляпунов көрсеткішін былай табуға болады
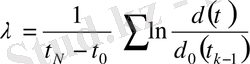 . (13)
. (13)
Ляпунов көрсеткіші термині бойынша хаостың критериі мына түрде жазылады:
λ > 0 - хаостық қозғалыс, (14)
λ ≤ 0 - регулярлы қозғалыс.
x
y
z
t 0
d 0
t 1
d 1
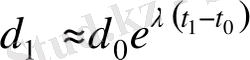
13-сурет. Ляпунов көрсеткішінің ең үлкен мәнін анықтауда қолданылатын екі көрші траекторияның арасындағы ара қашықтықтың өзгерісі
Бір өлшемді бейне үшін λ анықтайық:
х п+ 1 = f ( x n ) . (15)
f ( x ) функциясы тегіс әрі дифференциалданады, көрші траекториялар ара қашықтығы df / dx шамасымен өлшенеді. Бұған көз жеткізу үшін, бастапқы екі шарт енгіземіз: х 0 және х 0 + ε , онда (12) -қатынаста
d
0
=
 ,
,
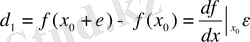 .
(16)
.
(16)
(13) -қатынас бойынша Ляпунов көрсеткішін (немесе сипаттық көрсеткішті) былай анықтаймыз
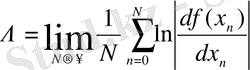 . (17)
. (17)
Мысал ретінде (3) логистикалық бейнеленуді қолданамыз. MatLab пакетінде r басқарушы параметрінен Ляпунов көрсеткішінің тәуелділік графигін саламыз (14-сурет) . Бұл программа төменде келтірілген. Ол үшін келесі m-файлдарды құрамыз:
- fotbr. m- логистикалық бейнелеу функциясының сипаттамасы;
- fdotbr. m- логистикалық бейнелеу функциясының туындысын табатын функцияның сипаттамасы;
% логистикалық бейнелеудің
% fotbr. m файл-функцияның листингі
function xn1 = fotbr(xn, r)
xn1 =r* xn*(1-xn) ;
% fdotbr. m файл-функцияның листингі (логистикалық
% бейнелеу функциясының туындысы) :
function dx = fdotbr(dxn, r)
dx = r*(1-2*dxn) ;
%
 параметрге байланысты Ляпунов көрсеткішін
параметрге байланысты Ляпунов көрсеткішін
% есептеуге арналған файл-сценарийдың листингі
NN = 1000;
r = [3. 0:0. 001:4. 0] ;
N = length(r) ;
L = zeros(1, N) ;
x = zeros(1, NN) ;
for j = 1:N
x (1) = 0. 1;
for i=2:NN
x(i) = fotbr(x(i-1), r(j) ) ;
end;
x = log(abs(fdotbr(x, r(j) ) ) ) ;
L(j) = sum(x) /NN;
end;
plot(r, L, 'k-') ;
xlabel('r') ;
ylabel('\lambda') ;
title('Логистикалық бейнелеудің …
Ляпунов көрсеткіші') ;
Басқару параметр r > 3, 57 болса, бейне хаосты күйге ауысады. Ляпунов көрсеткішін r параметрінің функциясы ретінде есептеп, бұған көз жеткізуге болады (14-сурет) . r > 3, 57 болғанда Ляпунов көрсеткіші 3, 57 < r < 4 периодтық терезелерде теріс болады.
3
3. 1
3. 2
3. 3
3. 4
3. 5
3. 6
3. 7
3. 8
3. 9
4
-4
-3. 5
-3
-2. 5
-2
-1. 5
-1
-0. 5
0
0. 5
1
r
λ
Логистикалық бейнелеудің Ляпунов көрсеткіші
14-сурет. Ляпунов көрсеткішінің r басқарушы параметріне тәуелділігі
Ляпунов көрсеткішінің ең үлкен мәнін табу . Әрбір динамикалық процесс үшін, ол уақыттан үздіксіз тәуелділіктегі траектория немесе уақыт бойынша дискретті эволюция болса да Ляпунов көрсеткіштерінің спектрі бар, ол фазалық кеңістікте ұзындық, аудан, көлемнің қалай өзгеретінін көрсетеді. Хаостың критериі ретінде Ляпунов көрсеткішінің тек ең ұлкен мәнін табу керек, ол көрші траекториялардың орташа жинақталмайтынын (λ > 0), не жинақталатынын (λ < 0) көрсетеді. Үлкен оң көрсеткіштің болуы хаостың критериі болып табылады.
Ляпунов көрсеткішін есептеудің екі жалпы тәсілі бар: біреуі белгілі дифференциалдық жүйе немесе айырымды теңдеулерден алатын мәліметтер үшін, екіншісі - тәжірибелік уақыттық қатарлардың мәндері үшін. [14] -жұмыста осы екі әдістің екеуі де қарастырылған, бірақ тәжірибелік мәндер бойынша Ляпунов көрсеткішін анықтауға арналған сенімді алгоритмді құру қосымша зерттеуді қажет етеді.
Келесі түрдегі дифференциалдық теңдеулерге арналған Ляпунов көрсеткішін анықтау әдісін қарастырайық
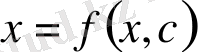 , (18)
, (18)
x - күйдің n айнымалылар жиынтығы, ал с - n параметрлер жиынтығы.
(13) -қатынасты қолданатын есептеулердің негізгі идеясы d ( t k ) /d ( t k-i ) траекториялар арасындағы ара қашықтықты анықтау . Әдістердің бірі (18) -теңдеулер жүйесін сандық интегралдауға негізделген. Алдымен тірек нәтиже алынады: x* ( t; x 0 ), мұнда x 0 - алғашқы шарт. Одан кейін әрбір t k уақыттың қадамында (18) -жүйе кез-келген бір алғашқы шарт ретінде алынған х* ( t k ) + η көрші нүктелермен қайта интегралданады. Бұдан басқа тура әдіс - (18) -теңдеуді белгіленген (тіректі) траектория х* ( t k ) маңайындағы өзгермелі траекториялардың вариацияларын табу. Осындай жағдайда әрбір уақыттық t k қадам үшін мына вариациялық теңдеуді шешеміз
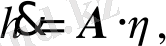 (19)
(19)
А - дербес туындылардың ∇ f ( x* ( t k ) ) матрицасы . А матрицаның барлық элементтері уақытқа тәуелді екенін атап өту қажет. Бірақ егер А матрицасы тұрақты болса, t k < t <t k+l интервалында η ( t ) шешімі бастапқы шартқа тәуелді болады. Егер бұл бастапқы шарт кездейсоқ таңдалса, онда А матрицасының ең үлкен оң өздік мәндеріне қарай η ( t ) құраушысы нөл емес ықтималдылықпен сипатталуы мүмкін. Бұл бағытта көрші траекториялардың аралықтарының өзгеруі ең үлкен Ляпунов көрсеткішін сипаттайтын болады.
Есептеу схемасы келесі түрде болады. (19) -теңдеуді интегралдап
x
*(
t
) табамыз. Әртүрлі өтпелі кезеңдерді ескермеу үшін, біраз уақыт күтіп,
d
(
t
) содан кейін есептейміз. Барлық өтпелі процестер сөніп және азайғаннан кейін
η
(
t
) табу үшін (20) -теңдеуді интегралдауға кірісеміз.
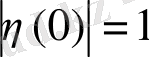 таңдауға болады, бірақ бастапқы бағыт кездейсоқ алынады. Одан кейін
таңдауға болады, бірақ бастапқы бағыт кездейсоқ алынады. Одан кейін
 =
А
(
х
*(
t
) )
η
теңдеулерді сандық интегралдаймыз,
x*
(
t
) себебінен
А
-дағы өзгерісін ескереміз. (Іс жүзінде (19) бен (20) -теңдеулерді қатар интегралдауға болады) . Берілген
t
k+
l
-
t
k
= τ
уақыт өткеннен кейін
=
А
(
х
*(
t
) )
η
теңдеулерді сандық интегралдаймыз,
x*
(
t
) себебінен
А
-дағы өзгерісін ескереміз. (Іс жүзінде (19) бен (20) -теңдеулерді қатар интегралдауға болады) . Берілген
t
k+
l
-
t
k
= τ
уақыт өткеннен кейін
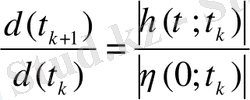 (20)
(20)
аламыз. (13) -те жаңа қадам бастау үшін, жаңа шарт ретінде η ( τ ; t k ) векторының бағытын таңдаймыз , яғни
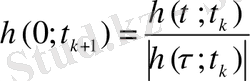 , (21)
, (21)
мұнда бастапқы ара қашықтық бірге нормаланған.
Осындай түрдегі есептеулер 15-суретте көрсетілген, мұнда инерциялы бейсызық Анищенко-Астахов генераторының теңдеуінің интегралдау нәтижесі m параметрінен функция ретінде алынған.
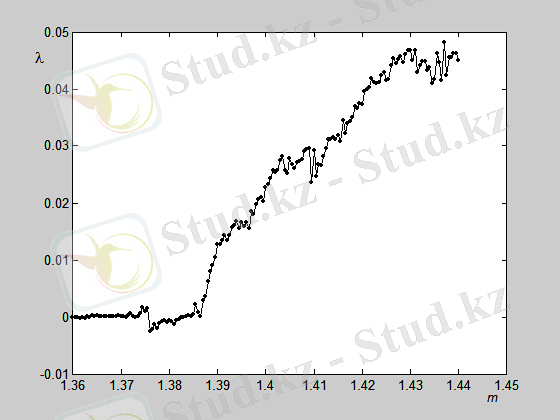
15-сурет. g = 0. 2 кезіндегі инерциялы бейсызық генератордың m параметрінен Ляпуновтың жоғарғы көрсеткішінің тәуелділігі
Төменде Ляпуновтың жоғарғы көрсеткішін есептеу үшін программалар мен қосымша файл-функциялардың листингтері келтірілген.
% 1-Листинг.
clear;
% параметрлер
m = [1. 36:0. 0005:1. 44] ; % m-ді өзгертеміз
% қалған параметрлер тұрақты
g = 0. 2;
d = 0. 001;
Nm = length(m) ;
Kart = zeros(Nm, 1) ;
% Ляпунов сипаттық көрсеткіштерін табамыз
% ЛСК (2- листингті қара )
for i = 1:Nm
Kart(i) = Lapun_var(m(i), g, d) ;
end;
figure(1) ;
% график тұрғызымыз
plot(m, Kart, 'k. ') ;
% 2-Листннг.
function Lap = Lapun_var(m, g, d)
%dfh = str2fun(dfname) ;
%clear;
dfh = @dfun_var; % диф. теңдеу файл-функциясының аты
% (3-листингті қара)
% бастапқы мәліметтер
% m = 2. 105;
% g = 0. 125;
% d = 0. 0001;
% gm = 0. 05;
% бастапқы мәндер
x0 = [0. 1 0. 0 0. 0 0. 0 0. 0 0. 0] ;
options=''; % ode45 үшін бос опция
% аттракторға шыққанша теңдеуді шешеміз
[t x] =ode45(dfh, [0 300], x0, options, m, g, d) ;
xv0 = [0. 0 0. 01 0. 0] ; % ұйтқу вектор үшін
% бастапқы мән
% ығысу векторының қалпы
eps = norm(xv0) ;
x0 = [x(length(x), 1:3) , xv0] ; %. диф. теңдеу
% үшін бастапқы мән
T = 50; % уақыт интервалы
N = 200; % итерация саны
L = ones(1, N) ;
for i= 1:1:N
% теңдеудің өзін және вариациядағы теңдеуді шешеміз
% t = T моментіне дейін
[t x] = ode45(dfh, [0 T], x0, options, m, g, d) ;
x0 = x(length(x), :) ;
xv0 = x0(4:6) ; % ұйтқу векторының
% соңғы мәні
x0m = norm(xv0) ; % оның нормасы
xv0 = xv0*(eps/x0m) ; % ұйтқу векторын
% қайта анықтаймыз
x0 = [x0(1:3), xv0] ; % келесі итерация үшін
% бастапқы мән
L(i) = x0m;
end;
Lap = sum(log(L/eps) ) /(N*T) ; % (ЛСК)
% 3-Листинг.
function dx = dfun_var(t, x, m, g, d)
dx = zeros(6, 1) ;
% теңдеудің өзі
dx(1) = (m-x(3) ) . *x(1) + x(2) - d. *x(1) ^3;
dx(2) = -1. *x(1) ;
dx(3) = g. *(Hev(x(1) ) . *x(1) ^2 - x(3) ) ;
% вариациялардағы теңдеу
dx(4) = m. *x(4) - x(6) . *x(1) - x(3) . *x(4) …
+ x(5) - 3*d*x(1) ^2*x(4) ;
dx(5) = -x(4) ;
dx(6) = 2*g*Hev(x(1) ) . *x(1) . *x(4) …
- g. *x(6) ;
... жалғасы- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz