Фракталдар және мультифракталдар теориясы: жалпыланған фракталдық өлшемдер мен мультифракталдық спектр


Мультифракталдар
Фракталдар және мультифракталдар теориясы қазір әртүрлі құбылыстарды түсіндіру үшін кең қолданады. Фракталдар санына мына обьектілер кіреді қатты кесілген формадағы сызықтар, беттер, денелер және олар кең масштабта қандай да бір қайталанушылыққа ие болады. Қайталану толық болуы мүмкін яғни толық ұқсас болады. ол Регулярлы фракталдар деп аталады. Ал кейде кездейсоқ болады оларды кездейсоқ фракталдар деп аталады. Фрактал дегеніміз - геометриялық обьект сызықтар, жазықтықтар, қатты бөлшектенген формадағы кеңістік денелері және олардың өзіне тән қасиеттері бар.
Табиғи фракталдардың қасиеттері тек l min ≤ l ≤ l max қатынасын қанағаттандыратын l масштабында ғана қарастырылады, .
Бұл шектеулер табиғи, өйткені біз мысал ретінде - бөлшектенген Броундық бөлшектің тегіс емес траекториясын келтірген кезде, бұл бейненің ашық идеализация екенін түсінеміз. Оның мәнісі мынада кішкентай масштабта массаның ақырғылығы мен Броундық бөлшектің өлшемі және де әсерлесу уақытының ақырғылығы деп айтылады. Осы жайттарды ескерсек Броундық бөлшектің траекториясы қисық болып шығатынын көреміз.
Нақ өзіне ұқсас қасиеттер тек қана реттелуші фракталдарға тән екенін атап өтуіміз керек. Ал егерде құраушыларының детерминиялық тәсілдерін кейбір ықтималдық элементтің құрылу алгоритміне қоссақ, онда кездейсоқ фракталдар пайда болады.
Өлшемділігі
d
(
d
= 1 - түзу,
d
= 2 - жазықтық,
d
= 3 - үшөлшемді кеңістік) болатын Евклид кеңістігінде өлшемі
L
шектелген
ℒ
аймағын алып жатқан фракталды объектіні қарастырайық. Фракталды объект өзінің құрылуының қандайда бір кезеңінде осы аймақта таралған
N
>>1 нүктелерден тұратын жиын болсын. Нүктелер саны
N
мейлінше
N
→
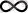 шекке жақын болсын. Барлық
ℒ
аймағын қабырғасы
δ
және көлемі
δ
d
куб ұяшықтарға бөлелік.
δ
азайған сайын,
N
(
δ
) ұяшықтар саны дәрежелік заңдылықпен өседі
шекке жақын болсын. Барлық
ℒ
аймағын қабырғасы
δ
және көлемі
δ
d
куб ұяшықтарға бөлелік.
δ
азайған сайын,
N
(
δ
) ұяшықтар саны дәрежелік заңдылықпен өседі
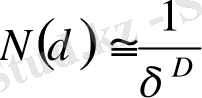 , (2. 9)
, (2. 9)
мұндағы D - Хаусдорф бойынша, немесе, фракталдық өлшемділік деп аталады.
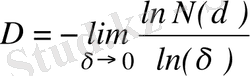 Сөйтіп,
Сөйтіп,
(2. 10) Табиғатта кездесетін фракталдар біртекті емес болып табылады, оларды мультифракталдар деп атайды. Мультифракталды әр қайсысы өзіндік өзұқсастық қасиеттеріне ие болған бөліктерге ажыратуға болатын объект деп айтуға болады. Сөйтіп, мультифракталды әр қайсысының өзіндік фракталдық өлшемділігі бар фракталдардың жиыны ретінде қарастыруға болады. Сондықтан мультифракталды сандық түрде сипаттау үшін жалғыз шама (жалғыз фракталдық өлшемділік) жеткіліксіз болады, бұл сипаттау фракталдық өлшемділіктердің спектрін білуді талап етеді. Оны есептеудің әдістері 3 тарауда қарастырылады.
2. 5 Фракталдық өлшемділік
Евклид кеңістігіндегі өлшемі L фракталдық объектіні қарастырайық. Мұнда біз тек, бос емес, яғни ішінде кем дегенде бір нүктесі бар ұяшықтарды ескереміз. Бос емес ұяшықтардың i нөмері i = 1, 2, . . . N ( δ ) аралығында өзгерсін, мұндағы N ( δ ) ұяшықтың δ өлшеміне тәуелді - бос емес ұяшықтардың жалпы саны. Егер ұяшықтар бойынша нүктелердің таралуы бір келкі болмаса фрактал біртексіз, яғни мультифрактал ретінде қарастырылады. Мультифракталды сипаттау үшін ℒ облысындағы берілген нүктелердің таралуын сипаттайтын D q жалпыланған фракталдық өлшемділіктер енгізіледі.
n i (δ) -i-ші нөмерлі ұяшықтағы нүктелер саны болсын, онда
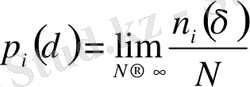 (2. 11)
(2. 11)
шамасы көп нүктелерден кездейсоқ алынған нүктелердің i -ші ұяшықта жататындығының ы (25)
мұндағы
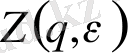 - жалпыланған статистикалық қосынды:
- жалпыланған статистикалық қосынды:
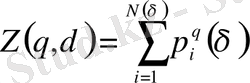 .
.
Егер
D
q
=
D
= const, яғни
q
-ға байланысты болмаса, бұл тек бір ғана шамамен -
D
фракталдық өлшемділікпен сипатталатын нүктелер жиыны жәй, регулярлы фрактал болады. Керісінше
D
q
функциясы
q
мен бірге өзгерсе онда қарастырылып отырған жиын мультифрактал болады.
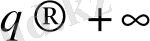 жағдайда (2. 1) жалпыланған статистикалық қосындыға ең көп
n
i
бөлшектері бар ұяшықтар көп ықпал етеді, сондықтан олар ең көп
p
i
толтырылу ықтималдығымен сипатталады. Керісінше
жағдайда (2. 1) жалпыланған статистикалық қосындыға ең көп
n
i
бөлшектері бар ұяшықтар көп ықпал етеді, сондықтан олар ең көп
p
i
толтырылу ықтималдығымен сипатталады. Керісінше
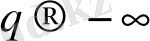 ұмтылғанда (26) жалпы статистикалық қосындыға ең аз толған ұяшықтар, яғни
p
i
-дің аз мәндері көп ықпал етеді. Осылайша,
D
q
функциясы, зерттеліп отырған
ℒ
нүктелер жиынының қаншалықты біртексіз екендігін көрсетеді
.
ұмтылғанда (26) жалпы статистикалық қосындыға ең аз толған ұяшықтар, яғни
p
i
-дің аз мәндері көп ықпал етеді. Осылайша,
D
q
функциясы, зерттеліп отырған
ℒ
нүктелер жиынының қаншалықты біртексіз екендігін көрсетеді
.
Жалпы жағдайда мультифрактал, статистикалық қосындының
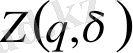 δ
→ 0 ұмтылғандағы қасиетін анықтайтын, қандайда бір
δ
→ 0 ұмтылғандағы қасиетін анықтайтын, қандайда бір
 бейсызық
(25) функциямен сипатталады. Бірақ нүктелердін таралуын сипаттау үшін
бейсызық
(25) функциямен сипатталады. Бірақ нүктелердін таралуын сипаттау үшін
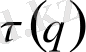 функциямен қатар оның туындысын да білу қаже т:
функциямен қатар оның туындысын да білу қаже т:
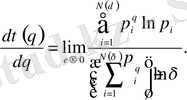 (2. 12)
(2. 12)
Бұл туынды q мен бірге өзгереді.
q = 1 болғанда жалпыланған фракталдық өлшем:
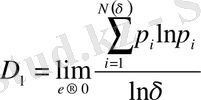 . (2. 13)
. (2. 13)
Бұл формуланың алымы, таңбасын ескергенде, фракталдық жиынның энтропиясы болып келеді. Нәтижесінде D 1 жалпыланған фракталдық өлшем S ( δ ) энтропиямен келесі қатынаста болады:
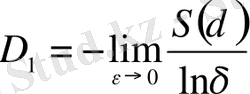 . (2. 14)
. (2. 14)
Бұдан,
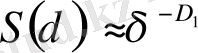 , (2. 15)
, (2. 15)
Яғни, D 1 дегеніміз нүктенің қандайда бір ұяшықта орналасу орнын анықтайтын информацияны сипаттайды. Осыған байланысты D 1 жалпы фракталдық өлшемділікті көп жағдайда информациялық өлшемділік деп атайды. Бұл δ ұяшықтың өлшемі нөлге ұмтылғанда, нүктенің орнын анықтау информациясы қалай өсетіндігін көрсетеді.
2. 6 Корреляциялық өлшемділік
Бірдей өлшемді
δ
ұяшықтарға бөлінген фракталды бетті қарастырайық және кез-келген х
1
және х
2
еркін таңдалған екі нүкте фракталды объектіге жататын нүктелер болсын делік.
.
Екі нүктеніңде
i
-ші ұяшықта болу ықтималдығы қанша? Бір нүктенің осы беттің
i
-ші элементіне түсу ықтималдығы
р
i
-ге тең. Егер екі нүктенің осы ұяшыққа түсуі байланыссыз оқиғалар деп алсақ, онда оның ықтималдығы
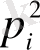 -ге тең болады.
-ге тең болады.
Фракталдық бет ( q = 2) жабылатын ұяшықтар көлемін кішірейткендегі, статистикалық қосындының (26) өзгерісін қарастырайық. δ - ны кішірейткенде қосынды азаяды, бұдан ол дәрежелік заңға бағынады деп жорамалдауға болады:
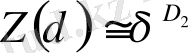 , (2. 16)
, (2. 16)
немесе, эквивалентті, шек
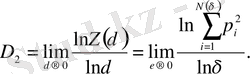 (2. 17)
(2. 17)
D 2 корреляциялық өлшемділік деп аталады.
2. 7 Мультфракталды спектрлік функция F( α )
D q шамасы жалпы қабылданған мағынасында нақты айтатын болсақ фракталдық өлшемділік емес. Сондықтан көп жағдайда мультифракталды жиынды бейнелеу үшін мультифракталды спектрлік функция f(α) (мультифракталдың сингулярлығының спектрі) қолданылады. Біз f ( α ) шамасы ℒ жиынындағы біртекті фракталдық ішкі жиынының хаусдорф өлшемділігіне (2) тең екендігін көрсетеміз .
Өзұқсас жиын үшін р i шамасының δ ұяшық өлшеміне тәуелділігі дәрежелік байланыста болады
 (2. 18)
(2. 18)
мұндағы α i - қандайда бір дәрежелік көрсеткіш (шынында әр-түрлі i ұяшыққа әр-түрлі) . Регулярлы (бірқалыпты) фракталдар үшін α i дәрежелік көрсеткіштер бірдей және D фракталдық өлшемділікке тең
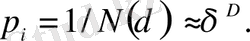 (2. 19)
(2. 19)
Бұл жағдайда (26) статистикалық қосынды келесі түрге өзгереді
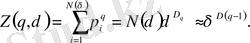 (2. 20)
(2. 20)
Сондықтан
 және барлық жалпыланған фракталдық өлшемділіктер
D
q
=D
бұл жағдайда бір-біріне сәйкес келеді және
q
-ға байланысты емес
.
Бірақ мультифрактал сияқты күрделі объектілер үшін
р
i
ұяшықтардың толтырылу ықтималдығы бірдей емес және
α
i
дәреже көрсеткіші әр-түрлі. Көп кездесетін жағдайдың бірі - осы мәндер қандайда бір (
α
min
,
α
max
) жабық интервалды толтырады және
және барлық жалпыланған фракталдық өлшемділіктер
D
q
=D
бұл жағдайда бір-біріне сәйкес келеді және
q
-ға байланысты емес
.
Бірақ мультифрактал сияқты күрделі объектілер үшін
р
i
ұяшықтардың толтырылу ықтималдығы бірдей емес және
α
i
дәреже көрсеткіші әр-түрлі. Көп кездесетін жағдайдың бірі - осы мәндер қандайда бір (
α
min
,
α
max
) жабық интервалды толтырады және
 (2. 21)
(2. 21)
Осы
α-
ның шектік мәндерімен
τ
(
q
) функциясының туындысы мәндерінің арасындағы байланысты, атап айтқанда
q
→±
 ұмтылғандағы туындының шектік мәндерін қарастырайық. Егер біз
q
→
ұмтылғандағы туындының шектік мәндерін қарастырайық. Егер біз
q
→
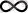 мәнін алсақ, (2. 10) тендеудегі
i
бойынша қосындыға, максималды
р
max
толықтыру ықтималдығымен сипатталатын тек ішінде көп нүктелер шоғырланған ұяшықтар көп үлес береді. Қосындыда тек осындай (саны
N
max
) ұяшықтарды қалдыра отырып, (2. 10) теңдеудің алымы
N
max
мәнін алсақ, (2. 10) тендеудегі
i
бойынша қосындыға, максималды
р
max
толықтыру ықтималдығымен сипатталатын тек ішінде көп нүктелер шоғырланған ұяшықтар көп үлес береді. Қосындыда тек осындай (саны
N
max
) ұяшықтарды қалдыра отырып, (2. 10) теңдеудің алымы
N
max
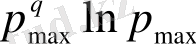 , ал бөлімі
N
max
, ал бөлімі
N
max
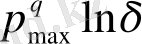 екендігін көреміз
.
Соңында,
екендігін көреміз
.
Соңында,
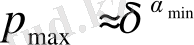 екенін ескерсек, ізделіп отырған туындының шегі
α
min
-ға тең болады. Сол сияқты,
q
→-
екенін ескерсек, ізделіп отырған туындының шегі
α
min
-ға тең болады. Сол сияқты,
q
→-
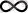 , жағдайда (2. 10) теңдеудегі қосындыны үшін
р
min
ықтималдықпен сипатталатын тек аз нүтелері бар ұяшықтарды ескеру қажет. Бұл жағдайда
, жағдайда (2. 10) теңдеудегі қосындыны үшін
р
min
ықтималдықпен сипатталатын тек аз нүтелері бар ұяшықтарды ескеру қажет. Бұл жағдайда
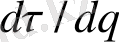 туындысы
α
max
мәніне ұмтылатыны анық.
туындысы
α
max
мәніне ұмтылатыны анық.
Сонымен біз маңызды қорытындыға келеміз:
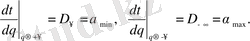 (2. 22)
(2. 22)
яғни мүмкін болатын
α
интервалы,
q
→±
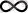 жағдайда жалпыланған фракталдық өлшемділіктің
D
q
шектік мәндерімен анықталады.
жағдайда жалпыланған фракталдық өлшемділіктің
D
q
шектік мәндерімен анықталады.
- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz