Мультифракталдық талдау: Dq өлшемдері, f(α) спектрі және сигнал энтропиясын нормалау


2. 1. Негізгі түсініктер
Фрактал деп өз-өзіне ұқсас қасиеті бар қисық формаға ие сызықтар, беттерді айтады. Фрактал сөзі латынның “fractus” сөзінен шыққан. Фракталдың өз-өзіне ұқсастық қасиеті фракталдың ең негізгі қыры болып табылады. Егер, үлкейтіп көретін болсақ, фракталдың кішкене фрагменттерінің үлкеніне ұқсайтынын көреміз [2, 3] .
Айталық, тура өз-өзіне ұқсастық қасиеті тек регулярлы фракталдарға ғана тиесілді. Егер детерминді құрылу әдісінің алгоритміне бір кездейсоқтық элементін қосатын болсақ, онда біз кездейсоқ фрактал аламыз. Олардың регулярлы фракталдардан негізгі айырмашылығы мынада. Өз-өзіне ұқсастық қасиеті тек объектінің статикалық тәуелсіз байқалуларының орташалануынан кейін болады.
Мультифракталды сипаттау үшін бір ғана емес, көп фракталдық өлшемділіктер жиыны керек. Табиғи фракталдар-дың көбі, негізінде, мультифракталдар. Қысқаша айтқанда, мультифрактал ол-біртекті емес фрактал болып табылады.
Жоғарыда айтқандай, регулярлық фракталдарға қарағанда бір ғана фракталдық өлшемділік D ғана емес, шексіз осындай фракталдық өлшемділіктер жиынымен ғана түсіндіруге болады. Осындай фракталдар статикалық қасиеттерге де ие болады.
Фракталдық өлшемділік
Ол L өлшемді Евклид кеңістігінде өлшемділігі d (d = 1-сызық, d = 2 - жазықтық, d=3-үшөлшемді кеңістік) белгілі бір шектік аумағын қамтитын фракталдық объектіні қарастырайық. Оның құрылу барысының белгілі бір кезеңінде ол N>>1 нүктелерден құралған жиынды берсін. Біз соңында N

 болады деп болжам жасаймыз.
болады деп болжам жасаймыз.
 l
ауданының көлемі
δ
d
және
δ
жағы бар кубтық ұяшықтарға бөлеміз.
δ
азайған сайын ауданды қамтитын
N
(
δ
), ұяшықтар саны дәрежелік заң бойынша өзгереді.
l
ауданының көлемі
δ
d
және
δ
жағы бар кубтық ұяшықтарға бөлеміз.
δ
азайған сайын ауданды қамтитын
N
(
δ
), ұяшықтар саны дәрежелік заң бойынша өзгереді.
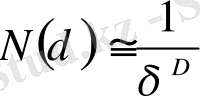 (2. 1)
(2. 1)
D дегеніміз хаусдорф немесе фракталдық өлшемділік деп аталады. (2. 1) -ді логарифмдеп және δ нөлге ұмтылса, оны былай жазамыз
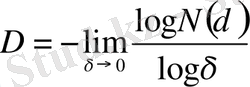 (2. 2)
(2. 2)
D-шамасы қарастырып отырған объектінің локалдық сипаттамасы болып табылады [3] .
Евклид кеңістігіндегі L өлшемді фракталдық объектіні қарастырамыз. Біз енді тек аз дегенде бір нүкте болатын бос емес ұяшықтарды қараймыз. Бос емес i ұяшықтар санының нөмірі i = 1, 2, . . . N ( δ ) арасында өзгерсін. Мұндағы, N ( δ ) - δ ұяшық нөмірінің өлшеміне тәуелді бос емес ұяшықтардың саны. Егер ұяшықтар бойынша нүктелер үлестірілуі бірдей болмаса, ондай фракталды біртексіз фрактал дейміз. Мультифракталды сипаттау үшін D q жалпыланған фракталдық өлшемділіктерді еңгіземіз.
Егер n i ( δ ) i нөміріне сәйкес ұяшықтағы нүктелер мөлшері болса, онда
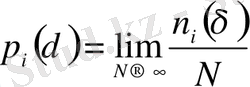 (2. 3)
(2. 3)
p i ( δ ) - жиыннан кездейсоқ таңдап алынған нүктенің i ұяшығында болу ықтималдылығы. Кеңейтілген фракталдық өлшемділіктер спектрі D q келесі қатынаспен анықталады
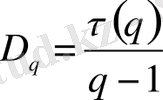 (2. 4)
(2. 4)
мұндағы
q
-
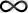 <
q
+
<
<
q
+
<
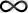 интервалында кез-келген мән қабылдайды, сонда
интервалында кез-келген мән қабылдайды, сонда
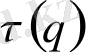 мына түрде жазылады
мына түрде жазылады
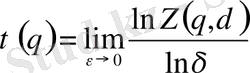 (2. 5)
(2. 5)
мұндағы
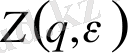 - кеңейтілген статикалық сумма:
- кеңейтілген статикалық сумма:
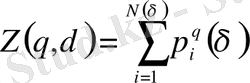 . (2. 6)
. (2. 6)
Егер
D
q
=
D
= const болса, яғни
q
дан тәуелді болмаса, онда мұндай нүктелер жиынын бір ғана D фракталдық өлшемділігі бар қарапайым, регулярлы фрактал деп атаймыз. Керісінше, егер
D
q
функциясы
q
бойынша өзгеретін болса, оны мультифрактал дейміз.
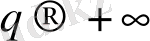 кезде кеңейтілген статикалық суммаға (2. 6) тек ең көп бөлшектері бар ұяшықтар саны басты үлес қосады. Оның толтырылу ықтималдылығы
p
i
болып табылады. Осыған орай
D
q
функциясы
кезде кеңейтілген статикалық суммаға (2. 6) тек ең көп бөлшектері бар ұяшықтар саны басты үлес қосады. Оның толтырылу ықтималдылығы
p
i
болып табылады. Осыған орай
D
q
функциясы
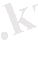 l
жиынындағы нүктелер санының біртексіздігін көрсетеді.
l
жиынындағы нүктелер санының біртексіздігін көрсетеді.
Жалпы жағдайда, мультифрактал
бейсызық
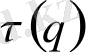 (2. 5) функциямен анықталады. Ол
δ
→ 0
(2. 5) функциямен анықталады. Ол
δ
→ 0
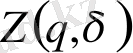 статикалық сумманы сипаттайды. Бірақ нүктелердің үлестірілуін тек
статикалық сумманы сипаттайды. Бірақ нүктелердің үлестірілуін тек
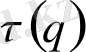 ғана емес, оның туындысы керек
ғана емес, оның туындысы керек
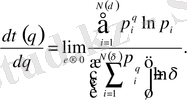 (2. 7)
(2. 7)
бұл туынды q мен бірге өзгереді.
q = 1 кезінде фракталдық өлшемділік мынаған тең
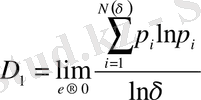 . (2. 8)
. (2. 8)
Бұл формуланың алымы фракталдық жиын энтропиясы болып табылады. Соңында, кеңейтілген фракталдық өлшемділік D 1 энтропиямен S ( δ ) мына қатынаспен сипатталады
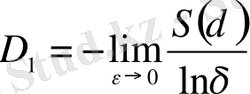 . (2. 9)
. (2. 9)
Жалпы түсінік бойынша D q шамалары, қатаң айтқанда, фракталдық өлшемділіктер емес. Сондықтан солармен бірге мультифракталдық жиынды сипаттау үшін мультифракталдық спектр функциясын f ( α ) қолданамыз. Оны мультифрактал сингулярлығының спектрі деп те атайды. Біз осы f ( α ) шамасын белгілі бір жалпы жиынның біртекті фракталдық L жиыншасының хаусдорфтық өлшемділігіне тең екенін көреміз. Ол q шамасын беру арқылы бүкіл статикалық суммаға үлкен үлесін қосады.
Өз-өзіне ұқсас жиындар үшін р i δ - ұяшық өлшеміне тәуелділігі дәрежелік мәнге ие болады:
 (2. 10)
(2. 10)
мұндағы α i - дәреже көрсеткіші (i- әр түрлі ұяшық үшін әрқалай) . Біртекті фрактал үшін α i дәреже көрсеткіштері бірдей және D фракталдық өлшемділігіне тең.
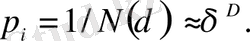 (2. 11)
(2. 11)
Бұл жағдайда статикалық сумма:
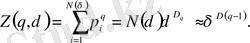 (2. 12)
(2. 12)
Сондықтан, бұл жағдайда,
 және барлық
D
q
=D
фракталдық өлшемділіктеріне сәйкес келеді және q-дан тәуелді болмайды. Бірақ күрделі объект, яғни, мультифрактал үшін ол олай болмайды. Оның біртексіздігін ескере отырып,
р
i
ұяшықтарының толтырылу ықтималдылығы бірдей емес және
α
i
әр ұяшық үшін дәреже көрсеткіші әр мәнді беретін болады. Кейін біз бұл мәндердің бір жабық интервалды толтыратындығына көз жеткіземіз (
α
min
,
α
max
), демек
және барлық
D
q
=D
фракталдық өлшемділіктеріне сәйкес келеді және q-дан тәуелді болмайды. Бірақ күрделі объект, яғни, мультифрактал үшін ол олай болмайды. Оның біртексіздігін ескере отырып,
р
i
ұяшықтарының толтырылу ықтималдылығы бірдей емес және
α
i
әр ұяшық үшін дәреже көрсеткіші әр мәнді беретін болады. Кейін біз бұл мәндердің бір жабық интервалды толтыратындығына көз жеткіземіз (
α
min
,
α
max
), демек
 . (2. 13)
. (2. 13)
Осы
α
мәндерінен
τ
(
q
) функциясының туындысы арасындағы байланысты көреміз. Дәлірек айтқанда,
q
→±
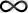 . Болғандағы осы туындының “шегін” көреміз. Егер біз
q
→
. Болғандағы осы туындының “шегін” көреміз. Егер біз
q
→
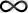 деп алсақ, онда
i
бойынша суммалау кезінде тек ең көп орналасқан ұяшықтар үлес қосады. Әр ұяшық
р
max
максималды толтырылу ықтимадылықтарымен сипатталады. Суммада тек (саны
N
max
) (2. 7) -гі алымы
N
max
деп алсақ, онда
i
бойынша суммалау кезінде тек ең көп орналасқан ұяшықтар үлес қосады. Әр ұяшық
р
max
максималды толтырылу ықтимадылықтарымен сипатталады. Суммада тек (саны
N
max
) (2. 7) -гі алымы
N
max
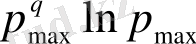 , ал бөлмі
N
max
, ал бөлмі
N
max
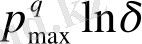 -ға тең болады деп ескерсек, онда іздеген туынды шегіміз
α
min
-ге тең болғанын көреміз.
-ға тең болады деп ескерсек, онда іздеген туынды шегіміз
α
min
-ге тең болғанын көреміз.
Соған ұқсас егер
q
→-
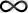 болса, онда (2. 7) суммалағанда тек ықтималдылығы
р
min
болатын ең аз орналасқан ұяшықтарды ескеру керек. Бұл жағдайда,
болса, онда (2. 7) суммалағанда тек ықтималдылығы
р
min
болатын ең аз орналасқан ұяшықтарды ескеру керек. Бұл жағдайда,
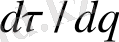 -қа ұмтылғандығы мәлім. Сонымен қатар, біз негізгі шешімге келеміз, мұнда
-қа ұмтылғандығы мәлім. Сонымен қатар, біз негізгі шешімге келеміз, мұнда
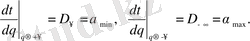 (2. 14)
(2. 14)
Яғни,
α
болатын мәндерінің интервалы жалпылама фракталдық өлшемділік-тердің шектік мәндерімен анықталады (
q
→±
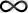 кезінде) .
кезінде) .
Енді α i -дің әр мәндерінің ықтималдылық үлестірілуіне келейік. n ( α ) dα
α i -дің α мен α + dα арасында болу ықтималдылығы болсын. Басқаша айтқанда, n ( α ) dα p i α i өлшемдеріне ие осы интервалда жататын белгілі бір салыстырмалы ұяшықтар саны. α i -дің әр мәндері D бірдей емес, әр түрлі f ( α ) дәреже көрсеткіштерінің мәндеріне ие болады.
.
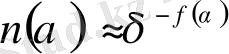 (2. 15)
(2. 15)
Осыған орай,
f
(
α
) функциясының мағынасы бір
L,
жиынның біртекті фракталдық жиыншасының
L
α
өлшемділігін білдіреді. Ол
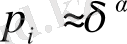 ұяшықтардың толтырылуының бірдей ықтималдылықтарын білдіреді. Жиынның фракталдық өлшемділігі сол жиынның фракталдық өлшемділігіне
D
0
тең не аз екендігін
f
(
α
) функция үшін мына теңсіздік көрсетіп тұр:
ұяшықтардың толтырылуының бірдей ықтималдылықтарын білдіреді. Жиынның фракталдық өлшемділігі сол жиынның фракталдық өлшемділігіне
D
0
тең не аз екендігін
f
(
α
) функция үшін мына теңсіздік көрсетіп тұр:
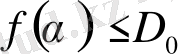 . (2. 16)
. (2. 16)
Қорытындысында, біз мынадай шешімге келдік. f ( α ) функциясының әр түрлі мәндерінің жиыны біртекті L α жиыншаларға бөлінген L жиынының фракталдық өлшемділіктер спектрі болып табылады. Осыдан, мультифрактал термині түсінікті бола бастайды. Оны L α жиыншаларға бөлінген L жиынының әр түрлі біртекті фракталдар қосындысы деп түсінуге болады. Олардың әрқайсысында өзінің f ( α ) фракталдық өлшемділіктері болады.
Демек, әр жиыншаға тек бар ұяшықтар N ( δ ) санының тек бір бөлігі ғана тиесілі болады. Ықтималдылықтарды нормалау шарты:
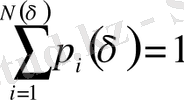 (2. 17)
(2. 17)
тек бір ғана жиынша бойынша ықтималдылық орындалмайды. Ол онда бірден аз болып қалады. Сондықтан,
α
i
мәнге сәйкес
р
i
ықтималдылық
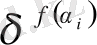 шамасынан аз болады. Ол шама осы жиыншаны құрайтын ұяшықтар санына кері пропорционал. Қорытындысында, біз
f
(
α
) үшін келесі негізгі теңсіздікке келеміз. Яғни,
α-
ның барлық мәні үшін
шамасынан аз болады. Ол шама осы жиыншаны құрайтын ұяшықтар санына кері пропорционал. Қорытындысында, біз
f
(
α
) үшін келесі негізгі теңсіздікке келеміз. Яғни,
α-
ның барлық мәні үшін
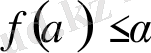 (2. 18)
(2. 18)
Теңдік белгі тек толық біртекті фракталға ғана тән, мұндағы f ( α ) = α = 0 [4] .
Сигналдың аффиндік коффициенті мен энтропиясы
x(t) радиосигналының біртексіздігі сандық бойынша метрлік сипатта-
мамен, яғни аффиндік коэффициентпен сипатталады. Ол әр импульс форма-
ларының айырмашылығын сипаттайды. Метрлік сипаттамалары (ұзындық, аудан, көлем) Коши-Буняковский теңсіздігінен шығады:
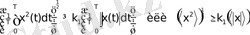 (2. 19)
(2. 19)
мұндағы, t мен T өтіп жатқан және сипаттамалық уақыт мағынасын біл-
діреді. Мұндай теңсіздік орындалады, егер
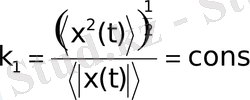 (2. 20)
(2. 20)
Радиофизикада k 1 шамасын импульстік сигнал формасының коэффициенті деп атайды. (2. 19) теңсіздігі кез-келген х 1 (t), х 2 (t) функция үшін Гелдердің интегралдық теңсіздігінен шығады:
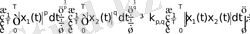
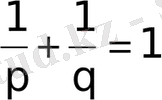 (2. 21)
(2. 21)
- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz