Херст көрсеткіші мен нормаланған құлаш әдісі: фракталдық өлшем және Пуанкаре бейнесі арқылы динамикалық хаосты диагностикалау


Нормаланған құлаш әдісі
Табиғи процестерді бақылаулардың көбісі уақыт бойынша өлшеулердің қатарларын құрайды. Мысалы, ауа температурасын өлшеудің ұзақ қатарлары болады. Олардан жылдық вариацияларды анық байқауға болады. Қысқа және ұзақ уақыт аралығында температураны өлшегенде оның ретсіздігі байқалады. Температура сияқты, өзендердің құатын, тұнбалардың мөлшерін, ағаштар сақиналарының жуандығын тағы да уақыт бойынша өзгеретін көптеген процестерді нормаланзан құлаш әдісі арқылы зерттеуге болады немесе оны Херст әдісі деп де атайды. Херст өмір бойы Нил өзенін зерттеумен және су қорларының қалыптасуымен байланысқан есептерді шешумен шұғылданған. Ол ашқан жаңа статистикалық нормаланған құлаш әдісі «Долговременное на- копление: экспериментальное исследование» деген кітапта толық суреттелген. Жоғарыдағы аталған өлшеулердің заңдылықтары Н көрсеткішімен (Херст көрсеткішімен) сипатталады.
Кез келген шаманың уақыттық жиыны (тәжирибе нәтижелері) х(і) болсын. х шаманың максимал және минимал мәндерінің айырымы құлаш деп аталады жэне ол К әріпімен белгіленеді:
max x t ,
min x t , ,
\<{<т \<1<Т " 4 У
мунда і - бүгін сандарды қабылдайтын дискретті уақыт, т - қарастырылған уақыт аралығының узақтығы. Қулаш қарастырылған г периодына тэуелді жэне К г-ға байланысты өседі.
к/8 өлшемсіз қатынасты қолданып, әр түрлі қүбылыстардың құлаштарын салыстыруға болады, мүнда £ - стандартты ауытқу, яғни дисперсияның квадрат түбірі:
x t
x
Көптеген уақыт қатарларының к/8 нормаланған қүлашы төмендегі эмпириялық қатынаспен жақсы сипатталады
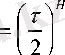 (3)
(3)
к
~8
(3) -формула нормаланған қүлаш әдісінің негізі болып табылады. Табиғаттың сапасы әр түрлі қүбылыстарына Херст көрсеткішінің Н = 1/2, Н > 1/2 мәндері сәйкес келеді. Радиоэлектроникада Херст әдісі фазаның ауытқуы, жиіліктің ығысуы сияқты винер процестерін сипаттау үшін қолданады.
Херст көрсеткіші Н арқылы В жергілікті және аумақты фракталды өлшемділікті анықтауға болады
£> = -, В = 2-Н . (4)
н у 7
Хаусдорф-Безикович өлшемділігі, немесе фракталды өлшемділік Ә объектің, процестің интегралды сипаты болып табылады. Ол евклид геометриялық өлшемділігін жалпылайды және оған қарағанда бүтін емес мәндерді қабылдай алады. Фракталды өлшемділік ұғымының танымдылық кү ш і мынада: оның көмегімен зерттелініп жатқан процестерді хаосты немесе күрделілік қасиеттері бойынша реттеуге және оларды сұрыптауға (бөлуге) болады.
Фракталды сызықтары 0<Ж0. 5 аймаққа сәйкес процестерді
антиперсистенті деп атайды және оларға ауыспалы тенденция және шуылдың салыстырмалы жоғарғы деңгейі тән. Фракталды сызықтары 0. 5<Ж1 аймаққа сәйкес процестерді персистентті деп атайды және оларға бақыланған тенденцияның сақталынуы және шуылдың салыстырмалы төмен деңгейі тән. Н = 0. 5 болғанда нақты сипаты жоқ, ал шуыл дәрежесі Херст әдісімен ескеруге болмайтын факторлармен анықталатын процестер орын алады. Көп жағдайда, барлық стационарлық сигналдардың фракталды сызықтары Н = 0. 5 түзумен бірігеді.
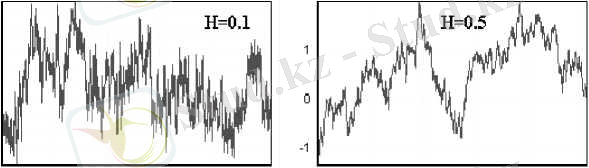
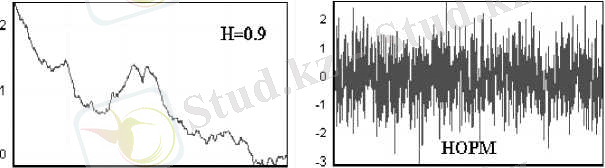
Сигналдардың шуыл дәрежесімен және олардың фракталды қасиеттерімен, Херст көрсеткішімен (Н) сипатталған жалпы заңдылықтары 1-суретте көрсетілген. Ол жерде әр түрлі фракталды қасиеттері бар және оған сай Херст көрсеткішінің әр түрлі мәні бар уақыт қатарларының жиыны кескінделген (таңдама көлемі Ж1000) .
200 400 600 800 1 000 200 400 600 800 1 000
200 400 600 800 1 000 200 400 600 800 1 00
1-сурет. Н = 0. 1; Н = 0. 5; Н = 0. 9 бар фракталды уақыт қатарлары және қалыпты
ықтималдың таралуы бар ақ шуылдың типтік көріністері
Визуалды түрде стационар кездейсоқ сигналдар (мысалы, қалыпты таралуы бар шуыл) максимал шуыл екенін анықтауға болады, ал фракталды сигналдардың шуылы Херст көрсеткіші өскен сайын төмендейді.
ДИНАМИКАЛЫҚ ХАОСТЫҢ СИПАТТАМАЛАРЫ
Біз бұл дәрісте динамикалық жүйе қозғалысының хаосты әлде реттелген болуын қалай анықтайтынын қарастырамыз. Қозғалыс режимдерінің ауысуына сай параметрлердің “күдікті” (кризистік) мәндерін анықтау ламинарлы ағыстың турбулентті ағысқа өткенде сұйықтықтардың түтқыр ағысының аумалы жылдамдығын табу есебіне ұқсас. Бұл жылдамдық сипаттамалық ұзындыққа көбейтіліп және сұйықтықтың кинематикалық түтқырлығына бөлініп нормаланған түрінде - Рейнольдс саны (Ке) ретінде белгілі. Ғасырдан астам уақыт инженерлер мен физиктер Ке шамасының нақты теориялық мәнін таба алмады, сондықтан гидромеханиканың көптеген есептері үшін (Ке) криз эксперимент жүзінде анықталады. Осы сияқты механикалық және электрлік жүйелерде хаостың пайда болу критерийлері тәжірибе немесе сандық модельдеу арқылы табылады. Осындай жүйелер үшін детерминдік хаос пайда болатын “күдікті” параметрлерді табу тәжірибе қоюшылар мен теориямен айналысатындардың да жұмысына қажет.
Физикалық жүйеде хаостың пайда болу критерийлері екі түрлі болады: болжамдық ережелер (хаостың тууын жорамалдайтын) және диагностикалық құралдар (хаостың не бар, не жоқ болуын анықтайтын) .
Хаосты тербелістерді жорамалдайтын болжамдық ережесі деп хаосқа тудыратын басқарушы параметрлердің жиынтығын анықтайтын критерийді айтамыз. Физикалық жүйеде хаостың пайда болуын болжау жүйенің жуықталған математикалық моделі (одан критерий шығаруға болатын), немесе көптеген тәжірибелер жүзінде жинақталған мәлімет болуға байланысты. Хаостың туындайтынын болжайтын негізгі болжамдық моделге периодтың екі еселену критериі, гомоклиникалық траекторияның бар болу критериі мен консервативті хаостың резонанстарының бір-бірінен асып түсуі (Чириков критериі) сондай-ақ, алмасу және өтпелі критерийі жатады.
Хаостық тербелістердің диагностикалық критериі деп өлшеулер нәтижесінде немесе мәліметтерді өңдеу арқылы зерттелетін жүйе хаостық динамика күйінде болатындығын анықтайтын тесті атайды. Біз келесі диагностикалық сипаттамаларды қарастырамыз: Ляпунов көрсеткішін және фракталдық өлшемділікті (6-бөлім) . Қазіргі кезде әр түрлі фракталдық өлшемділіктермен объектілерді зерттеу және оларды модельдеу тек физиктер мен программистердің айрықша құзіреті ғана емес, әр түрлі ойламаған қолдану тапты. Фракталдық модельдің физикада қолдану жетістігі, біріншіден, көптеген процестер мен объектлердің фракталдық заңдылығының болуы. Егер зат таза газ күйінде немесе кристалл күйінде болмаса, онда ол сипаттық масштабтарының кейбір диапазондарында фракталдық қүрылымға ие болады. Көптеген реттелмеген процестердің модельдері кездейсоқ тық-тың, немесе,
динамикалық хаостың әр түрлі варианттарына негізделеді, олар да фракталдық қасиетке ие.
Қазіргі уақытта фракталдар мен олардың қолдануларына арналған көптеген әдебиет бар. Фракталдар тақырыбына өте көп әдебиет бар болса да, олардың жалпы анықтамасы жоқ. Біз [11] -кітапта келтірілген қысқа анықтаманы қолданамыз: цүрылымдыц, иерархиалық өзүцсас цүрылымы бар объектілерді фракталдар деп атайды. Фракталдың геометриялық сипаттамаларының өзгерісі заттардың тегіс еместігін, олардың кещстік-уақыттық құрылымын білдіреді. Объектінің фракталдық қасиеттерін 6-бөлімде талқылаймыз.
Бұл бөлімде хаостық тербелістер пайда болатын белгілі физикалық жүйелер мен математикалық модельдер үшін тәжірибе, сан арқылы анықталатын критерилерін қарастырамыз. Бұл критерилер физикалық және сандық тәжірибелер арқылы анықталады. Біз осындай жағдайдарды екі себепті талдаймыз. Біріншіден, хаостық тербелістерді зерттеген, хаостық тәртібі бар бірнеше жүйемен танысу пайдалы, сол арқылы қандай жағдайда хаос туатыны анықталады. Осындай қарапайым жағдайлар күрделі жүйелерде хаостың пайда болу шарттарын түсінуге көмектеседі. Екіншіден, теориялық критерилерді белгілеген кезде теорияны тәжірибемен салыстыратын қандай да бір тест қажет.
Пуанкаре бейнесі
Динамикалық жүйелерге математикалық өңдеу жасағанда [х(һ), х(і 2 ), . . . , х(і„), . . . , х(і^) } мәліметтердің уақыттық іріктелуін бейне деп атайды, ол үшін осындай белгілеу енгізілген: х п = х(і п ) . Қарапайым детерминдік бейнеде х п+1 шамасын х п мәні бойынша табуға болады. Бұны көбінде мынадай түрде жазады:
 (1)
(1)
Х п + 1 =/*п
Бұндай жазылудан айырымдық теңдеуді тануға болады. Бейне ұғымы бұдан да көп айнымалыларға жалпыланады. Осылай, х п - М компонентті вектор бола алады; х^= (Үіп, Ү2п, -Үш ), сонда (1) -теңдеу М теңдеулерден тұратын жүйе болады.
Мысалы, [х(і), х (і) ] фазалық жазықтығында бейнеленген бөлшектің қозғалысын қарастырамыз дейік. Егер қозғалыс хаосты болса, онда траектория фазалық кеңістікті толтыруға тырысады. Бірақ, егер біз қозғалысты үздіксіз бақыламай, динамикалық сипаттамаларын тек жеке кезеңдерде тіркесек, одна қозғалыс фазалық кеңістіктің нүктелер тізбегімен беріледі (1-сурет) . Егер х п =
х(і п ) жэне у п = х(і п ), онда фазалық кеңістіктің бүл нүктелер тізбегі екі өлшемді бейнені береді
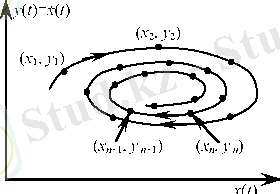
1-сурет. Пуанкаре бейнесінің схемалық суреті
Х п + 1 =/( Х п, УпХ
(2)
у п+ 1 =ё( х „, у п ) -
Егер і п іріктеу уақыты белгілі ережеге бағынса, бұл бейне Пуанкаре бейнесі деп аталады.
Жеке бейсызық жүйелер үшін Пуанкаре бейнесін таза күйінде табу өте қиынға түседі (тек дифференциалдық теңдеуді аналитикалық жолмен шешкен жағдайларда мүмкін) . Біз Пуанкаре бейнесін логикалық теңдеу үшін тұрғызамыз.
Популяцияның өсуінің ең қарапайым моделі логикалық теңдеу болып табылады:
Х +1 =/а(1-х„), п = \2, . . . , Н, (3)
мұнда х п - физикалық өлшемнің байқалуы, г - басқарушы параметр. Төменде логикалық теңдеудің шешімін іске асыру, Пуанкаре программасы және сәйкес графиктер келтірілген (2, Зсуреттер) . МаІЬаЬ жүйесі арқылы алынған.
% Логикалық теңдеу және Пуанкаре бейнесін % салуға арналған файлдың листингі
сіеаг;
N = 1000 ;
М = 850 ; г = 4 ; һ = 0 . 01 ; х( 1 ) = 0 . 1 ;
£ог і = 1^-1
х(і+1) = г. *х(і) . *(1-х(і) ) ;
епгі
3 = М^;
£ідиге( 1 ) р 1оһ(х(^) ) ; т = 1 ^- 1 ;
£ідиге( 2 )
р 1оһ(х(т), х(т+1), ’. ’) ;
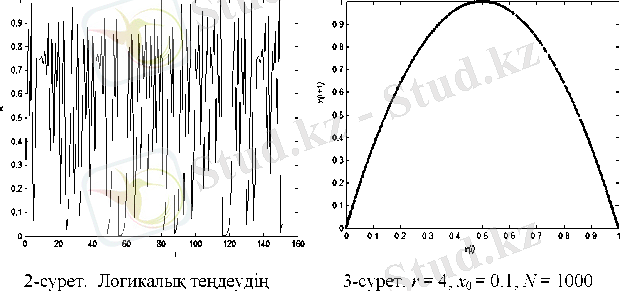
нәтижесі үшін логикалық теңдеудің
Пуанкаре бейнесі
Мәжбүр тербеліс жүйесі үшін Пуанкаре бейнесі. Т периодты мәжбүр қозғалыс кезінде Пуанкаре бейнесін алу үшін і„ = пТ + п 0 іріктеуін жасау қажет. Бұл периодты қозғалысты периодты емес қозғалыстан айыру үшін қажет. Мысалы, гармониялық қозғалыстың іріктеуін өз периодымен синхрондасақ, онда «бейнелеу» фазалық кеңістікте екі нүктемен беріледі. Егер периоды 3-ке тең субгармоника байқалса, Пуанкаре бейнесі 3 нүктеден тұрады.
Тағы да бір хаостық емес Пуанкаре бейнелеуі 4-суретте көрсетілген, мұнда қозғалыс екі шамаласпайтын жиіліктегі тербелістерді білдіреді:
х<3= С г зіп( со г і + д . х ) + С 2 зіп( со 2 і + сі 2 ), (4)
со^ / со 2 - иррационалдық сан. Егер периоды бір жиілікке сәйкес келетін іріктеу жасасақ, онда траектория үздіксіз фигура тәрізді, немесе фазалық кеңістіктегі
ДХ
х
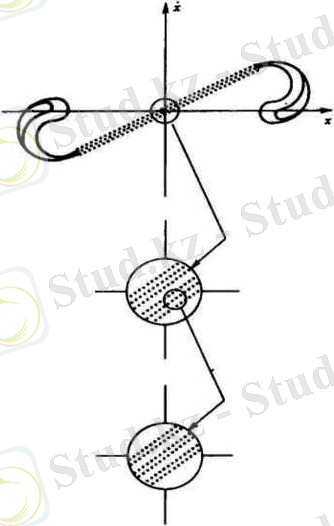
4-сурет. Магнит күштерімен пайда болған потенциалдық қос шұңқырында
тербеліп тұрған, периодты сигналмен қоздырылған екі еркіндік дәрежелі
біліктің квазипериодты қозғалысына сәйкес кедетін фазалық кеңістіктегі
Пуанкаре бейнесі
орбита болып түседі. Бұндай қозғалысты кейде периодтыққа жақын немесе квазипериодты, немесе «тор үстіндегі қозғалыс» деп аталады, бұлар хаосты емес. Егер Пуанкаре бейнесі шекті нүктелер жиынтығынан да, тұйықталған орбитадан да (4-суретті қара) тұрмаса, онда қозғалыс хаосты болу мүмкін (5- сурет) . Өшусіз, немесе сәл өшпелі жүйелер үшін хаосты қозғалыстың Пуанкаре бейнесі көбінесе фазалық кеңістікте реттелмеген нүктелер жиынтығы түрінде болады (5-а, сурет) . Өшпелі жүйелерде Пуанкаре бейнесі кейде қатаң реттелген шексіз нүктелер жиынтығындай болады, олар 6-б, в суретте көрсетілгендей параллельді сызықтарға ұқсас шоғырланады. Сандық модельдеу арқылы Пуанкаре бейнесінің белгілі бөлігін үлкейтіп (6 сурет), бүдан да жіңішке құрылымды көруге болады. Бірнеше үлкейтулерден кейін нүктелер жиынтығының құрылысы сақталса, онда қозғалыс сипаты әуейі аттрактор дейді. Осыған ұқсас құрылымдары бірінің ішіне бірі енгізілген жиындарды канторлық көбейтінділер деп атайды. Тербелістердің уақыт эволюциясын білдіретін Пуанкаре бейнесінде канторлық көбейткіштер сияқты құрылымдардың пайда болуы хаостық қозғалыстың айқын индикаторы болады.
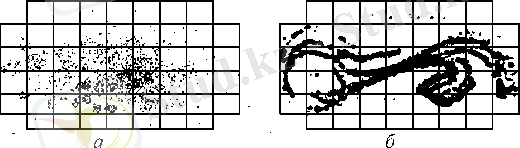

в
5-сурет. Ұзынынан иірілген біліктің хаостық қозғалысы үшін Пуанкаре бейнесі:
а) - әлсіз өшуі бар;
б), в)
- қатты өшу кезінде әуейі аттрактордың фракталдық
құрылымы байқалады
- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz