Сигналдарды фракталдық және мультифракталдық талдау: фракталдық өлшемділік пен корреляциялық өлшемділікті есептеу әдістері


Өлшемділігі
d
(
d
= 1 - түзу,
d
= 2 - жазықтық,
d
= 3 - үшөлшемді кеңістік) болатын Евклид кеңістігінде өлшемі
L
шектелген
ℒ
аймағын алып жатқан фракталды объектіні қарастырайық. Фракталды объект өзінің құрылуының қандайда бір кезеңінде осы аймақта таралған
N
>>1 нүктелерден тұратын жиын болсын. Нүктелер саны
N
мейлінше
N
→
 шекке жақын болсын. Барлық
ℒ
аймағын қабырғасы
δ
және көлемі
δ
d
куб ұяшықтарға бөлелік.
δ
азайған сайын,
N
(
δ
) ұяшықтар саны дәрежелік заңдылықпен өседі
шекке жақын болсын. Барлық
ℒ
аймағын қабырғасы
δ
және көлемі
δ
d
куб ұяшықтарға бөлелік.
δ
азайған сайын,
N
(
δ
) ұяшықтар саны дәрежелік заңдылықпен өседі
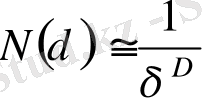 , (34)
, (34)
мұндағы D - Хаусдорф бойынша, немесе, фракталдық өлшемділік деп аталады. (1) қатынасты логарифмдеп және δ -ны нөлге ұмтылдыру арқылы келесі қатынасты аламыз
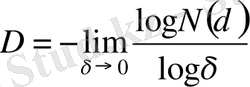 . (35)
. (35)
Логарифмді кез-келген оң, бірден өзгеше негіз бойынша алуға болады, мысалы, 10 немесе
 бойынша. (2) формула
D
фракталдық өлшемділіктің жалпы анықтамасы болып табылады. Бұл формулаға сай
D
шамасы берілген объектінің локальды сипаттамасы болып табылады. Егер бұл анықтаманы Кантор жиыны (1-сурет) немесе
бойынша. (2) формула
D
фракталдық өлшемділіктің жалпы анықтамасы болып табылады. Бұл формулаға сай
D
шамасы берілген объектінің локальды сипаттамасы болып табылады. Егер бұл анықтаманы Кантор жиыны (1-сурет) немесе
1
1/3
1/3
1/9
1/9
1/9
1/9
1/27…
7-сурет. Кантор жиыны
8 - сурет.
Серпиньскийдің
квадратты кілемі
Серпиньский кілемі (2-сурет) секілді фракталды объектілерге қолдансақ, онда D бөлшек шама болады.
Серпиньский кілемінің (2 сурет) фракталдық өлшемін табайық. Егер ұяшықтың өлшемі δ = 1/3 болса, онда беттегі ұяшықтар саны N = 8 болады, ұяшықтар ауданы үш есе азайғанда δ = 1/9 және N = 64 ұяшықтар санын аламыз, ал k- ші деңгейде - δ = (1/3) k және N ( δ ) = 8 k болады. (2) формуланы қолданып, келесі мәнді аламыз
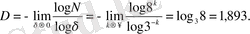
Алынған нәтижелерді қолдану мүмкіндігін көрсету үшін Вейерштрасс-Мандельброттың өзаффинді фракталдық қисықтарын b , A параметрлерінің әртүрлі мәндері үшін қарастырайық:
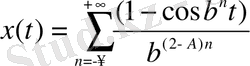 . (36)
. (36)
Ұзындығы
L
(
δ
) қисықпен шектелген
F
(
δ
) фракталдық ауданды бөліп алу схемасы 3-суретте көрсетілген. Жаңа
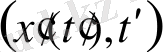 тікбұрышты координат жүйесі,
x
(
t
) мен
тікбұрышты координат жүйесі,
x
(
t
) мен
 өсінің қыйылысуы әр-түрлі күрделі құрылымдары бөліп алатындай етіп таңдалған. Екі қатар тұрған нөлдер интервалда
өсінің қыйылысуы әр-түрлі күрделі құрылымдары бөліп алатындай етіп таңдалған. Екі қатар тұрған нөлдер интервалда
 яғни
яғни
 ,
,
 өсіне симметриялы қыйсық тұрғызайық. Бұл процедура, мәндер өсі бойынша түзу сызық болмайтын,
өсіне симметриялы қыйсық тұрғызайық. Бұл процедура, мәндер өсі бойынша түзу сызық болмайтын,
 параметрімен сипатталатын тұйықталған фракталдық қисықты алуға мүмкіндік береді. Осындай әр-түрлі мәндері бар фракталдық элементтерді бөле отырып
параметрімен сипатталатын тұйықталған фракталдық қисықты алуға мүмкіндік береді. Осындай әр-түрлі мәндері бар фракталдық элементтерді бөле отырып
 фракталдық өлшемділіктің асимптотикалық мәндерін іздестіруге болады. Басқа жағдайларда
T
-ға тәуелді фракталдық өлшемділік туралы ғана айтуға болады.
фракталдық өлшемділіктің асимптотикалық мәндерін іздестіруге болады. Басқа жағдайларда
T
-ға тәуелді фракталдық өлшемділік туралы ғана айтуға болады.
 айнымалыларды
айнымалыларды
 ретінде қайта белгілеу арқылы (16), (17) формуланы қолданамыз. 4-суретте (15-17), (22) формулалармен табылған
D
1
және
D
2
мәндері көрсетілген. Вейерштрасс-Мандельброт өзіндік аффинді қисығы әртүрлі фракталдық өлшемділіктерге ие. Өзұқсастық (
D
1
және
D
2
мәндерінің тепе-теңдігі)
А
параметрінің үлкен мәнінде
ретінде қайта белгілеу арқылы (16), (17) формуланы қолданамыз. 4-суретте (15-17), (22) формулалармен табылған
D
1
және
D
2
мәндері көрсетілген. Вейерштрасс-Мандельброт өзіндік аффинді қисығы әртүрлі фракталдық өлшемділіктерге ие. Өзұқсастық (
D
1
және
D
2
мәндерінің тепе-теңдігі)
А
параметрінің үлкен мәнінде
 ,
γ
*
= S
*
(
I
) = 0. 806 ғана бола алады. Екінші өзіндік ұқсастылық критерийі
γ
*
=
f
*
(
I
) = 0. 567 мұнда байқалмайды, себебі бұл қисықтар үшін
,
γ
*
= S
*
(
I
) = 0. 806 ғана бола алады. Екінші өзіндік ұқсастылық критерийі
γ
*
=
f
*
(
I
) = 0. 567 мұнда байқалмайды, себебі бұл қисықтар үшін
 мәні жоғары.
мәні жоғары.
10-сурет. Фракталдық өлшемділіктің (22) формуладағы
А
параметіріне тәуелділігі. (
b
= 1, 5) .
 -
D
1
,
-
D
1
,
 -
D
2
-
D
2
D 1 , 2
1. 806
t'
T i
9-сурет. Өзаффинді Вейерштрасс-Мандельброт қыйсығы.
b = 1. 5, A = 1. 8
1
1, 2
1, 4
1, 6
1, 8
2
2, 2
1
2
3
4
5
A
Біз өзаффинді жиындарды фракталдық өлшемділік арқылы сандық сипаттау мүмкіндігін көрсеттік. Көп өлшемді фракталдық шама арқылы анықталатын фракталдық өлшемділік теңдеулері, күрделі геометриялық объектілердің форма коэффициенті, өзаффинді фракталдардың реттік параметрлерін енгізу мүмкіндіктері осы бөлімдегі негізгі нәтижелер болып табылады. Өлшеу масштабы азайған жағдайда локальды реттілік параметрі өседі, ал өлшеу масштабы өскен жағдайда глобальды параметрдің реттілігі өседі. Үздіксіз фракталды қисықтың симметриясының өзгеруі екінші реткі фазалық көшу секілді. Бұл кризистік құбылыстарды фракталдық өлшемділіктер арқылы физикалық (концентрация, температура, қысым т. с. с) параметрлер арасындағы байланысты сипаттауға мүкіндік береді.
Корреляциялық өлшемділік
Бірдей өлшемді
δ
ұяшықтарға бөлінген фракталды бетті қарастырайық және кез-келген
х
1
және
х
2
еркін таңдалған екі нүкте фракталды объектіге жататын нүктелер болсын делік.
.
Екі нүктеніңде
i
-ші ұяшықта болу ықтималдығы қанша? Бір нүктенің осы беттің
i
-ші элементіне түсу ықтималдығы
р
i
-ге тең. Егер екі нүктенің осы ұяшыққа түсуі байланыссыз оқиғалар деп алсақ, онда оның ықтималдығы
 -ге тең болады.
-ге тең болады.
Фракталдық бет ( q = 2) жабылатын ұяшықтар көлемін кішірейткендегі, статистикалық қосындының (26) өзгерісін қарастырайық. δ -ны кішірейткенде қосынды азаяды, бұдан ол дәрежелік заңға бағынады деп жорамалдауға болады:
 , (37)
, (37)
немесе, эквивалентті, шек
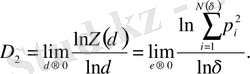 (38)
(38)
D 2 корреляциялық өлшемділік деп аталады.
Корреляциялық өлшемділіктің бейсызық динамикадағы ерекшелігі оны есептейтін салыстырмалы жеңіл және эффективті (басқа өлшемділіктерге қарағанда жеңіл және эффективті) тәсілі бар, ол - Грассбергер-Прокаччи алгоритмі .
... жалғасы- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz