Астрофизикалық объектілер мен галактикалардың фракталдық өлшемділігінің алмаспалы эволюциялық модельдері

Пән: Автоматтандыру, Техника
Жұмыс түрі: Материал
Тегін: Антиплагиат
Көлемі: 3 бет
Таңдаулыға:

Өлшемділіктің фракталдық эволюциясы.

Астрофизикалық объектілер, галактикалар эволюция барысында алмаспалы құрылымға ие тербелістер жасайды. Алмасу деп - тұрақты және тұрақты емес тербелістердің жүйелі түрде бір - бірімен алмасуын атаймыз.

Осыған ұқсас алмаспалы процесстер сызықты емес, тепе теңдігі жоқ, ашық жүйелерде жүзеге асады. Яғни өзұйымдықтың пайда болуына себепті жағдайлар туады. Өзұйымдық процесі өзұқсас динамикалық қасиеттерге ие. Оның фазалық бейнесі ғажап (фракталды) аттрактор бола алады [76] .

Кейбір параметрдің уақыт бойынша эволюциясын қарастырайық, x(t) - фракталдық өлшемдікпен байланысты (өлшенетін жиынтықпен сипатталатын аддитивті шам(а), кейбір функция модулі:

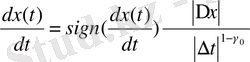(2. 15)

осында 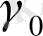- t мәнінің жиынтығының статистикалық сипаттамасы. Оны енгізу 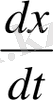туындасын шектейтін Лифшиц - Гельдер шартын қанағаттандыру мақсатымен себептеледі. Салыстырмалы 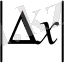өсімше модулін ( 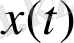мөлшерін өлшеу маштабы) фракталдық өлшемділік шартына сәйкс 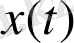алмастырамыз:

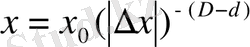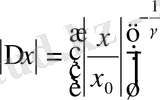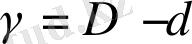, , (2. 16)

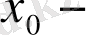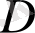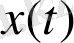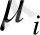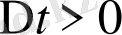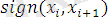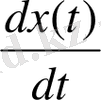бұл жерде, фракталды емес тұрақты өлшемділік, - мәндер жиынының фракталдық өлшемділігі, d - топологиялық өлшемділік. (2. 16) формуласын (2. 15) формуласына қойып дискретті айырмаға өтеміз. Белгілік функцияның дискретті түрін арқылы белгілейміз. Әрқашан да болуына сәйкес, sign( $\frac{dx_{i + 1}}{dx_{i}}$ ) белгілік функциясы тек қана 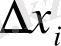дан тәуелді. Оның дискретті i айнымалысы бойынша өзгерісін келесі түрде анықтаймыз:

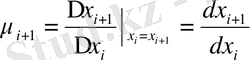(2. 17)

Әдетте 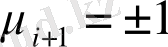мәні ұйытқулар эволюциясын сызықты сипаттауға қолданылады. Біз 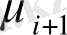ді 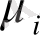арқылы анықтап, бұл шама модуліне шек қоймаймыз.

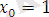
(2. 16), (2. 17) формулаларын ескеріп (2. 15) формуласын 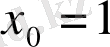жағдайы үшін келесі түрде жазамыз:

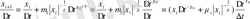
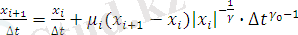(2. 18)

(2. 18) формуласында, уақыттың бірдей мезеттерін таңдау мүмкін болуы үшін 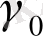шамасын ескермейміз. Дискретті есептеу алгоритмі бойынша 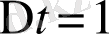деп алудың алдында, біз 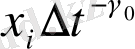мәнін 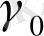арқылы моделдейміз: себебі осы ғана шама 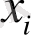мәндерінің хаотизациясына сәйкес келеді.

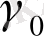шамасын енгізу мәні келесі шартты қанағаттандыруда екенін ескерсе:

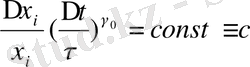(2. 19)

осында, τ - процесстің сипатты уақыты.

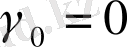кезінде, біз есептеуді 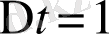, болатын өлшемділіктің Риман бойынша есептелу жағдайына келер едік. Ал 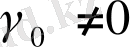деп таңдап алсақ, 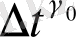ның 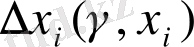функциясының өсімшесіне тәуелділігін ескере отырып, өлшемділіктің Лебег бойынша есептелуіне келеміз:

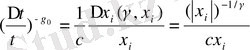(2. 20)

бұл жерде 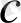- кейбір тұрақты сан. 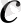ның мәнін сигнал спектірін сипаттауға арналған, сигнал базасының (күрделігінің) аналогы ретінде түсіндіруге болады:

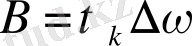(2. 21)

бұл жерде, - корреляцияның сипатты уақыты, 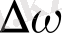- жиеліктер енділігі.

Анықтамаға сәйкес 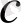- хаостық сигналды сипаттау үшін таңдалған дәлдік күрделігін сипаттайды. Фракталдық объектінің өлшемділігі бақылау дәлдігіне тәуелді, сондықтан да теория нәтежесіне 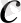тұрақтысы енеді. 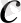шамасының мәні процессті бақылауға таңдалған 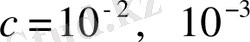және т. с. с дәлдіктің дәрежесіне сәйкес келеді. Егер де туынды таңбасы (2. 15) формулада сыртқы шарттармен анықталса (шуыл тәріздес әсерлер), ал (2. 19) формулада , 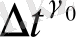абсолют мәндері таңдалады.

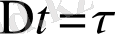деп, (2. 18) теңдікті келесі түрде көшіріп жазамыз:

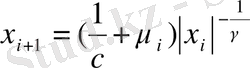(2. 22)

(2. 22) өрнекті дифференциалдап:

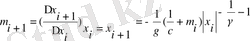(2. 23)

аламыз. (2. 22) және (2. 23) формулалар ізделіп отырған алмасудың бейнелеуін береді.

Алынған нәтежені ескере отырып, [77] сүйенсек, келесі өрнектерді аламыз:

$x_{i + 1} = (\frac{1}{C} + \mu_{i}) \left y_{i} \right^{- \frac{1}{\gamma_{x}}}$

$\mu_{i + 1} = - \frac{1}{\gamma x}\left( \frac{1}{C} + \mu_{i} \right) \left y_{i} \right^{- \frac{1}{\gamma_{x}} - 1}\$ (2. 24)

$y_{i + 1} = {1 - x_{i}/y_{i}}^{{- \gamma}_{y}}$

$x_{i + 1} = (\frac{1}{C} + \mu_{i}) \left y_{i} \right^{- \frac{1}{\gamma_{x}}}$

$\mu_{i + 1} = - \frac{1}{\gamma x}(\frac{1}{C} + \mu_{i}) \left y_{i} \right^{- \frac{1}{\gamma_{x}} - 1}$ (2. 25)

$y_{i + 1} = {1 - 1/x_{i}}^{{- \gamma}_{y}}$

(2. 24) және (2. 25) формулалар универсал алмасудың шарттарын қанағаттандыратын моделдік теңдеулер.

мұндағы xi, yi-аддитивті физикалық өлшемдер, γ- xi фракталдық өлшемділіктің бөлшектік бөлігі, 1/C-бақылаудың дәлдігі, 𝜇𝑖- мультипликатор.

Егерде бұл теңдеулерді галактикаларды модельдеуге қолданатын болсақ, айнымалылы параметірлерге басқаша түсінік беруге болады:

$x_{i}$ және $y_{i}$ аддитивті шамалар болғандықтан, оларды құрылымдық элементтер ретінде қарастыру мүмкін. Басқаша айтқанда галактиканы құрайтын жұлдыздардың кеңістікте таралу координаттары ретінде қабылдаймыз. γх, γy параметрлері галактиканың осьтері бойынша мультифракталдық өлшемділік көрсеткіші мағынасын береміз.