Плазма қасиеттерін астрофизикалық құбылыстарды түсіндіруге қолдану

Пән: Астрономия
Жұмыс түрі: Материал
Тегін: Антиплагиат
Көлемі: 6 бет
Таңдаулыға:

Плазма қасиеттерін астрофизикалық құбылыстарды түсіндіруге қолдану

Ғарыштағы заттың барлығы дерлік - жұлдыздар да, жұлдызаралық орта да, әртүрлі дәрежеде иондалған күйде болады, яғни плазма күйінде кездеседі.

Плазмада еркін оң және теріс зарядталған бөлшектер бар болғандықтан, оған бейтарап газда да әсер ететін қысым градиентінен басқа, магнит өрістері де әсер етеді. Бейтарап газдан тағы бір маңызды айырмашылығы - плазманың зарядталған бөлшектері өздерінің электр өрістері арқылы үлкен қашықтықтарда (тек тікелей соқтығулар кезінде емес) әсерлеседі. Бұның бәріне байланысты плазма күйіндегі зат көптеген жаңа қасиеттерді иеленеді де, оны зерттейтін арнайы әдістері қажет болады. Плазмадағы көп құбылыстарды түсіну үшін жарамды, одан әрі өте пайдалы болып магниттік гидродинамика жуықтауы табылады, сондықтан ол астрофизикада кең қолданылады. Магнитгидродинамика электрөткізетін орталардың ( плазманың, сұйық металдардың, электролиттердің ) магнит өрісіндегі қозғалысын оқып таниды. Сөйтіп, плазма физикасынан айырмашылығы - оның шеңберінде плазма электрондық және иондық сұйықтардың қоспасы, яғни тұтас орта ретінде қарастырылады да, плазма бөлшектерінің орталанған қозғалысы зерттеледі. Сондықтан бұл жуықтау (модель) тек “тығыз” плазманың қасиеттерін жақсы өрнектейді. “Тығыз” плазма деп бөлшектер соқтығысуының жиілігі жоғары, яғни бөлшектердің еркін жолы ұзындығы қозғалысының макроқасиеттері айтарлықтай өзгеретін қашықтыққа қарағанда аз, ал екі дәйекті (бірнен соң бірі болатын) соқтығысу арасындағы уақыт құбылыстардың сипатты ұзақтығынан аз болған плазма аталады.

әдеттегі гидродинамикадан айырмашылығы мынада: бейтарап газда басты қозғаушы күш болып қысым, дәлірек айтсақ, оның градиенті саналады. Ол температура мен тығыздыққа тәуелді және газдың көлемдік серпімділігін (сығылуға кедергісін) себептейді. Ал плазма бөлшектеріне қысым градиентінен басқа Лоренц күші әрекет етеді:

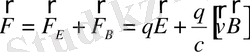, (3. 2. 1)

мұндағы 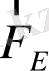- электр күші, 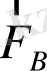- магнит күші, q - бөлшек заряды, с - жарық жылдамдығы, 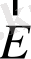- электр өрісінің кернеулігі, 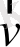- бөлшек жылдамдығы, 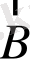- магниттік индукция.

Магнитгидродинамикада Лоренц күші барлық бөлшектер бойынша орталанады. Күштің орташа мәні j ток тығыздығына және магниттік индукцияға тура пропорционал. Зарядталған бөлшектер өз электр өрістерімен үлкен қашықтарда әрекеттеседі. Бұл әрекеттесу нәтижесінде болатын бөлшектер қозғалысындағы ауытқулар болшектер соқтығысуларының нәтижесі ретінде қарастырылады.

Электрондардың иондармен соқтығулары плазмада ағатын токтың энергиясының бір бөлігін жылулыққа айналдырады (токтың Джоуль өшуіне әкеледі) . Бұл өшу соқтығысулар жиілігіне тәуелді. Шапшаң электрондар иондармен соқтығысқанда баяулардан көрі аздау ауытқиды, сондықтан плазманың температурасы өскен сайын соқтығысулар саны, демек Джоуль өшуі де азайған сияқты болады.

Сан жағынан Джоуль өшуін плазманың σ өткізгіштігімен сипаттайды. Толығымен иондалған плазманың 1 см ³ көлемінде 1 с ішінде j ² /σ мөлшеріндегі Джоуль жылуы бөлінеді. Плазма өткізгіштігі тығыздығына тәуелсіз және температурасының 3/2 дәрежесіне пропорционал: σ ~T ^3/2 (металдарда керісінше болады: Т өскен сайын, кедергі өседі, ал σ азаяды) .

Ток өтетін бет үлкен келген жағдайда жалпы ток өте төмен болмаса да, ток тығыздығы аз болады. Демек, үлкен көлемдерде Джоуль өшуі де аз болады. Сипатты өлшемі R-ге тең плазма көлеміндегі өшу уақыты 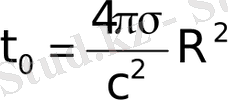(с), яғни плазма өткізгіштігі жоғарыламаған жағдайда да, плазманың алған көлемі үлкен болса, өшу уақыты өте үлкен болуы мүмкін. Ғарышта өлшемдері зеңгір плазма бұлттары кездеседі, олар үшін бұл қорытынды толығымен жарамды болып табылады. Ендігіде біз плазма өткізгіштігі шексіз не идеал дегенде, тек σ -ның өзі шексіз жағдайды емес, R өте үлкен жағдайды да, яғни, әйтеуір, t ₀ →∞ жағдайды айтамыз.

Сонымен, магнитгидродинамика жуықтауы шеңберінде одан да қатаң идеал өткізгіштік жуықтауы қолданылады. Ол t ₀ →∞ болғанда жарамды келеді. Оны қарастырайық.

Әуелі электрмагниттік индукция құбылысын есімізге түсірейік. Магнит өрісі қозғалып тұрған электр зарядтармен туғызылады және олармен әрекеттеседі. Бұнымен байланысты, тұйық өткізуші контурмен шектелген бет арқылы өтетін магниттік индукция ағыны өзгерсе, бұл контурда индукциялық электр тогы пайда болады және де индукциялық ток оны туғызатын себепке қарсы әрекет жасайтындай бағытталады (мысалы, индукция ағыны артса, ток онымен туғызылатын магнит өрісі бастапқы (сыртқы) магнит өрісіне қарама-қарсы бағытталған болатындай, яғни индукция ағынын бастапқы деңгейінде қалдыруға ұмтылатындай, бағытталған болады) . Бұл құбылыстың себебі түсінікті. Өзгеріп тұрған магнит өрісі құйындық электр өрісін туғызады, ал ол, өз кезегінде, зарядталған бөлшектерді қозғалтып, электр тогын туғызады. Өрістердің бағыттарын қарастырсақ (артып жатқан магнит өрісі оның бағытымен сол бұранданы, ал азайып жатқан магнит өрісі - оң бұранданы құрайтын электр өрісін тудырады), ток бағыты жөніндегі айтылған нәтижеге келеміз. Өздік индукция деген құбылыс та бар. Мысалы, өткізетін контур көзге қосылған болсын, яғни онда ток жүрсін. Контурды ажыратсақ, ток бірден тоқтамайды, өйткені тізбекте өтетін ток магнит өрісін тудырады және тізбекті ажыратқанда магнит өрісі жойыла бастайды, яғни контурмен шектелген бет арқылы өтетін магниттік индукция ағыны азая бастайды, сондықтан бұл азаюға қарсы әрекет жасайтын индукциялық ток пайда болады, ал мұндай токтың бағыты бастапқы токтың бағытымен бірдей болады. Сонымен, ажыратылған тізбектегі ток біртіндеп, тек өткізгіштің электр кедергісі болғанына байланысты, өшеді. Ал егер кедергі нөлге тең болса, яғни өткізгіштік шексіз болса, онда тізбекті көзден ажыратса да ток өзгермей аға берер еді, яғни магниттік индукция ағыны да өзгермейді. Демек, өткізгіштігі шексіз өткізгішпен шектелген бет арқылы өтетін магниттік индукция ағыны тұрақты болып табылады. Бұл, әрине, сапалы түрдегі түсіндіру, бірақ бұл нәтижені қатаң түрде де дәлелдеуге болады.

Алынған нәтижеге келудің тағы бір жолын қарастырайық. Дифференциалды түрдегі Ом заңын жазайық: j*=σE*, жұлдызшамен, плазмамен бірге қозғалып тұрған, яғни плазмаға қатысты тыныштық күйде тұрған санақ жүйесіне қатысты шамалар белгіленген. *-санақ жүйесіне қатысты электр өрісінің кернеулігін электрмагнит өрістерін түрлендірудің формуласын пайдаланып табуға болады:

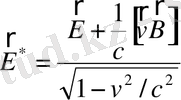, (3. 2. 2. )

мұндағы жұлдызшасыз шамалар лабораториялық санақ жүйесіне қатысты шамалар, 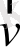- плазманың, яғни *-жүйесінің, лабораториялық жүйеге қатысты жылдамдығы. Ғарыштағы орта (плазма) әдетте жарық жылдамдығына жақын жалдамдықпен қозғалмайтынын еске алып, мұндай формуланы аламыз: 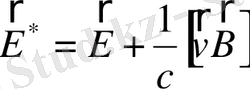. Енді мынадай мысал қарастырайық. Сыртқы біртекті емес магнит өрісінде плазма орналасқан болсын. Плазманы қозғалтсақ, *-жүйеде магнит өрісі өзгереді (жүйе кеңістікте өзгеретін магнит өрісінде қозғалса, жүйедегі бақылаушыға магнит өрісі уақыт бойынша өзгереді деп көрінеді), сондықтан бұл жүйеде құйынды электр өрісі ( ), демек j* да, пайда болады. Өткізгіштік шексіз болған жағдайда өте аз болса да (яғни, плазма аз, баяу қозғалса да), j* шексіздікке ұмтылады. Яғни, плазманы қозғалту үшін жұмсалған көп емес күш шексіз энергияның пайда болуына әкеледі, ал олай болмау тиіс. Демек, өткізгіштік идеал болған жағдайда қашанда да нөлге тең болуға тиісті. Бұл тек плазмадағы кез келген контур (плазма бөлшектерімен байланысты контур) арқылы магниттік индукция ағыны тұрақты болғанда орындалады. Бұл шарт жүзеге қалай асырыла алады? Мысалы, 3. 2- суреттегі конфигурациялы магнит өрісінде орналасқан өткізгіштігі идеал плазманың қозғалысы кезіндегі құбылыстарды қарастырайық.

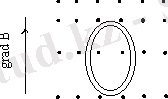
3. 2-сурет

Төмендегі суретте нүктелер магнит күш сызықтарын белгілейді, магнит өрісі жоғарыға қарай өседі. Плазма қозғалысы нәтижесінде плазмадағы қаланған контур көтеріңкі магнит өрісі аймағына ығысуы мүмкін (оң жақтағы сурет) . Бұл жағдайда контурмен шектелген бет арқылы өтетін күш сызықтарының саны, демек магниттік индукция ағыны, бастапқыға қарағанда көбейеді. Бірақ, жоғарыда көрсетілгендей,

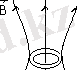
а) б)

3. 3-сурет

өткізгіштігі шексіз плазма жағдайында бұл ағын тұрақты болып қалу тиісті. Демек, плазма өткізгіштігі шексіз келсе, магниттік күш сызықтары плазма бөлшектеріне (элементтеріне) жапсырылған сияқты болып, бөлшектер артынан еріп жүру тиіс. Мысалы, бастапқы мезетте көрініс 3. 3 (а) -суреттегідей болып, ал одан кейін плазманың орта бөлігі сығылса (3. 3 (б) -сурет ), ортадағы контурмен шектелген бет арқылы өтетін күш сызықтар саны (демек магниттік индукция ағыны) бастапқыдағыдай қалу үшін, күш сызықтарының пішіні 3. 3 б) -суреттегідей , олар плазма бөлшектері артынан еріп жүрген сияқты болып, өзгереді. Бұдан идеал өткізгіштік жағдайда плазманың сығылуы ол орналасқан магнит өрісінің күшеюіне әкелетінін көруге болады.

Қарастырылған бұл құбылыс, яғни магниттік күш сызықтары бастапқы мезетте оларда орналасқан плазма бөлшектеріне бекітілген құбылысы, магнит өрісінің плазмаға қатырылуы деп аталады. Ол екі жолмен орындала алады.

Біріншісі, жоғарыда қарастырылғандай, плазма бөлшектері қозғалғанда, олар күш сызықтарын өздерімен бірге ертіп әкетеді. Әрине, күш сызықтары ойдағы сызықтар болып табылатынын ұмытпау керек. Шынында, плазманың біртекті емес магнит өрісіндегі қозғалысы нәтижесінде, не магнит өрісінің уақыт озғанымен өзгеруі нәтижесінде, магнит өрісін (магнит өрісі индукциясының үлестірілуін) өзгертетін индукциялық токтар пайда болады және де бұл өзгерістердің жалпы сипаты айтылған (плазма бөлшектері өрістің күш сызықтарын өзімен қоса ертіп әкететіндей) нәтижеге әкелетіндей болады.

Бірақ қатырылған күш сызықтары орта қозғалысы артынан кедергісіз ермейді. Сыртқы себептерден пайда болған ортаның қозғалыстары өрісті олардың кинетикалық энергиясы, не оларды қолдайтын қысым айырмасы магнит өрісінің энергиясынан көп болса ғана елеулі түрде өзгерте алады. Ал егер өріс басынан күшті болса, онда ортаның ретсіз қозғалыстары күш сызықтарының конфигурациясын айтарлықтай өзгерте алмайды, олар күш сызықтарын тек көп емес қисайта алады. Бұл жағдайда магнит өрісінің плазмаға қатырылуы күш сызықтары бөлшектер артынан еруімен емес, магнит өрісі бөлшектерге өз күш сызықтарынан кетуге мүмкіндік бермеуімен жүзеге асырылады (бұл - идеал өткізетін контурмен шектелген бет арқылы магниттік индукция ағынының тұрақтылығы қамсыздандырылуының екінші жолы) . Осы жағдайда бөлшектер тек магниттік күш сызықтары бойымен сырғи алады да, олардан шығып кете алмайды. Былайша айтқанда, магнит өрісі ортаның магниттік күш сызықтары бойымен емес жүзеге асатын қозғалыстарға бөгет болып шығады. Сондай-ақ егер бастапқы магнит өрісі аз болса, ал содан кейін орта қозғалыстары магниттік күш сызықтарын шиеленістірсе, онда ол сызықтар қоюлығының өсуіне, яғни магнит өрісінің күшеюіне әкеледі де, бір кезде магнит өрісі оның күш сызықтарын шиеленістіретін қозғалыстарға бөгет болуға жетерліктей өседі және бұл қозғалыстарды тоқтата бастайды.

... жалғасы

Сіз бұл жұмысты біздің қосымшамыз арқылы толығымен тегін көре аласыз.