Радиофизика негіздерін оқытуда бейсызық жүйелер мен динамикалық хаос теориясының әдістері


Динамикалық жүйелер ұғымы Ньютонның дифференциалдық теңдеулерімен сипатталатын механикалық жүйенің жалпыланған ұғымы түрінде пайда болды. Ол табиғаттың қай жүйесі болмасын: физикалық, химиялық, биологиялық, экономикалық т. б. қамтиды және тек детерминдік жүйелер ғана емес, стохастикалық жағдайларды да қарастырады. Динамикалық жүйені сипаттау әдістері әртүрлі. Олар -дифференциалдық теңдеулер, логикалық алгебра функциясы, графтар, марковтық тізбектер және т. б амалдар.
Қазіргі уақытта динамикалық жүйені бейнелейтін математикалық модельдердің екі түрі қолданылады.
1-ші көзқарас бойынша
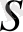 динамикалық жүйенің математикалық моделі қайсібір уақыт кезеңіндегі жүйенің
х
жағдайы қарастырылады және осы
х
жағдайдың уақыт бойынша өзгерісін анықтайтын
Т
операторы ұғымын пайдаланады.
Т
операторы келесі
динамикалық жүйенің математикалық моделі қайсібір уақыт кезеңіндегі жүйенің
х
жағдайы қарастырылады және осы
х
жағдайдың уақыт бойынша өзгерісін анықтайтын
Т
операторы ұғымын пайдаланады.
Т
операторы келесі
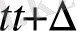 уақыт кезеңінде жүйенің
уақыт кезеңінде жүйенің
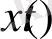 бейнелеуі бойынша
бейнелеуі бойынша
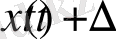 бейнелеуін орындау амалын көрсетеді. Егер
T
операторы уақытқа нақты тәуелді болмаса, онда
S
жүйесі
автономды
деп аталады, ал қарама-қарсы жағдайда - автономды емес.
S
жүйесінің
х
жағдайын Ф кеңістіктің біраз нүктесі ретінде, мысалы координаттармен, импульстармен, яғни
S
жүйесінің
фазалық кеңістігі
деп қарастыруға болады.
х
жағдайының өзгерісіне Ф фазалық кеңістіктегі
бейнелеуші
деп аталатын нүктелер қозғалысы жауап береді. Бейнеленген нүктелер қозғалысы
фазалық траектория
деп аталатын қисықты сипаттайды. Фазалық кеңістік Ф және оператор
T
динамикалық жүйенің математикалық моделін құрайды. Осындай әдіс динамикалық жүйелердің өзгерісін Ф фазалық кеңістіктің құрылымдық сипатын анықтау және осы құрылымының жүйенің физикалық параметрлерінің шамасына тәуелділігін анықтау арқылы сипаттайды.
бейнелеуін орындау амалын көрсетеді. Егер
T
операторы уақытқа нақты тәуелді болмаса, онда
S
жүйесі
автономды
деп аталады, ал қарама-қарсы жағдайда - автономды емес.
S
жүйесінің
х
жағдайын Ф кеңістіктің біраз нүктесі ретінде, мысалы координаттармен, импульстармен, яғни
S
жүйесінің
фазалық кеңістігі
деп қарастыруға болады.
х
жағдайының өзгерісіне Ф фазалық кеңістіктегі
бейнелеуші
деп аталатын нүктелер қозғалысы жауап береді. Бейнеленген нүктелер қозғалысы
фазалық траектория
деп аталатын қисықты сипаттайды. Фазалық кеңістік Ф және оператор
T
динамикалық жүйенің математикалық моделін құрайды. Осындай әдіс динамикалық жүйелердің өзгерісін Ф фазалық кеңістіктің құрылымдық сипатын анықтау және осы құрылымының жүйенің физикалық параметрлерінің шамасына тәуелділігін анықтау арқылы сипаттайды.
Физикалық жүйеде хаостың пайда болу критерийлері екі түрлі болады: болжамдық ережелер (хаостың тууын жорамалдайтын) және диагностикалық құралдар (хаостың не бар, не жоқ болуын анықтайтын) .
Хаосты тербелістерді болжау ережесі деп хаосты тудыратын басқарушы параметрлердің жиынтығын анықтайтын критерийді айтамыз. Физикалық жүйеде хаостың пайда болуын болжау жүйенің жуықталған математикалық моделі (одан критерий шығаруға болатын), немесе көптеген тәжірибелер жүзінде жинақталған мәлімет болуға байланысты. Хаостың туындайтынын болжайтын негізгі болжамдық модельге периодтың екі еселену критериі, гомоклиникалық траекторияның бар болу критериі мен консервативті хаостың резонанстарының бір-бірінмен қабаттасуы (Чириков критериі) сондай-ақ, алмасу және өтпелі критерийі жатады.
Хаостық тербелістердің диагностикалық критериі деп өлшеулер нәтижесінде немесе мәліметтерді өңдеу арқылы зерттелетін жүйе хаостық динамика күйінде болатындығын анықтайтын тесті атайды. Диагностикалық сипаттамалар: Ляпунов көрсеткіші және фракталдық өлшемділік. Фракталдық модельдің физикада қолдану жетістігі: көптеген процестер мен объектлердің фракталдық заңдылығының болуы.
Пуанкаре бейнесі
Динамикалық жүйелерге математикалық өңдеу жасағанда { х ( t 1 ) , х ( t 2 ), …, х ( t n ), …, х ( t N ) } мәліметтердің уақыттық іріктелуін бейне деп атайды, ол үшін мына белгілеу енгізілген: х n ≡ х ( t n ) . Қарапайым детерминдік бейнеде х n +1 шамасын х n мәні бойынша табуға болады. Бұны көбінде мынадай түрде жазады:
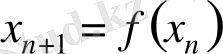 . (1)
. (1)
Бұндай жазылудан айырымдық теңдеуді тануға болады. Бейне ұғымы бұдан да көп айнымалыларға жалпыланады.
Мысалы, [
х
(
t
),
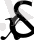 (
t
) ] фазалық жазықтығында бейнеленген бөлшектің қозғалысын қарастырайық дейік. Егер қозғалыс хаосты болса, онда траектория фазалық кеңістікті толтыруға тырысады. Бірақ, егер біз қозғалысты үздіксіз бақыламай, динамикалық сипаттамаларын тек жеке кезеңдерде тіркесек, одна қозғалыс фазалық кеңістіктің нүктелер тізбегімен беріледі (1-сурет) . Егер
х
n
≡
х
(
t
n
) және
у
n
≡
(
t
) ] фазалық жазықтығында бейнеленген бөлшектің қозғалысын қарастырайық дейік. Егер қозғалыс хаосты болса, онда траектория фазалық кеңістікті толтыруға тырысады. Бірақ, егер біз қозғалысты үздіксіз бақыламай, динамикалық сипаттамаларын тек жеке кезеңдерде тіркесек, одна қозғалыс фазалық кеңістіктің нүктелер тізбегімен беріледі (1-сурет) . Егер
х
n
≡
х
(
t
n
) және
у
n
≡
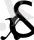 (
t
n
), онда фазалық кеңістіктің бұл нүктелер тізбегі екі өлшемді бейнені береді
(
t
n
), онда фазалық кеңістіктің бұл нүктелер тізбегі екі өлшемді бейнені береді
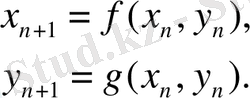 (1)
(1)
Егер t n іріктеу уақыты белгілі ережеге бағынса, бұл бейне Пуанкаре бейнесі деп аталады [1-5] .
( х 2 , у 2 )
( х 1 , у 1 )
( х n +1 , у n +1 ) ( х n , у n )
y ( t ) = x ( t )
.
х ( t )
1-сурет. Пуанкаре бейнесінің схемалық суреті
Жеке бейсызық жүйелер үшін Пуанкаре бейнесін таза күйінде табу өте қиынға түседі (тек дифференциалдық теңдеуді аналитикалық жолмен шешкен жағдайларда мүмкін) . Біз Пуанкаре бейнесін логикалық теңдеу үшін тұрғызамыз.
Популяцияның өсуінің ең қарапайым моделі логикалық теңдеу болып табылады:
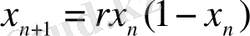 ,
,
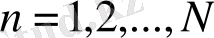 , (2)
, (2)
мұнда х n - физикалық өлшемнің байқалуы, r - басқарушы параметр. Төменде логикалық теңдеудің шешімін іске асыру, Пуанкаре программасы және сәйкес графиктер келтірілген (2, 3суреттер) . MatLab жүйесі арқылы алынған.
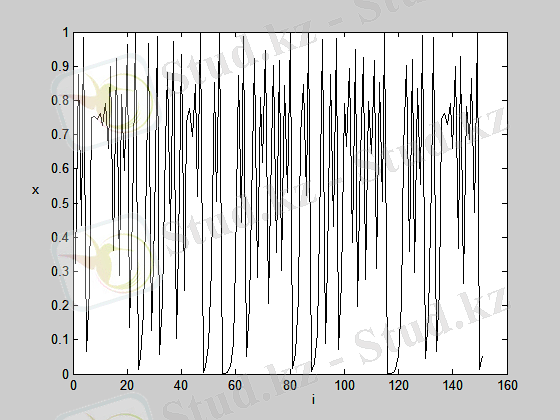
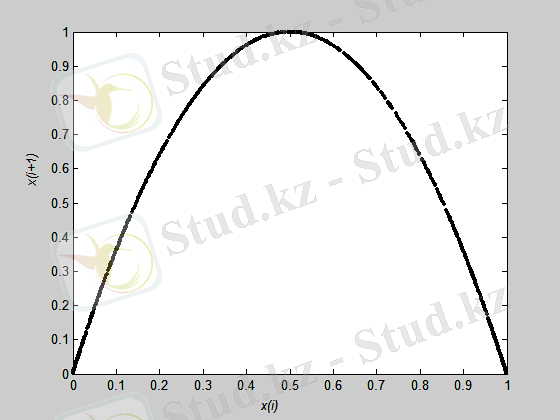
2-сурет. Логикалық теңдеудің нәтижесі
3-сурет. r = 4, x 0 = 0. 1, N = 1000 үшін логикалық теңдеудің Пуанкаре бейнесі
Бифуркациялық диаграммаларМатематикалық түрде біраз маңызды физикалық есептер параметрлерге байланысты дифференциалдық теңдеулерге сәйкес келеді. Параметрлердің өзгерісі қозғалыстың бір режимінің орнықтылығының жоғалтып, жүйенің басқа күйге өтуіне әкелу мүмкін. Мысал - параметр генерация табалдырығынан асқанда Ван-дер-Поль генераторында жаңа периодты қозғалыстың пайда болуы. Бұл құбылыс бифуркация деп аталады, ал ол болған кездегі параметрдің мәні - бифуркация нүктесі. Ең қажет бифуркациялар - бифуркация нүктесінен өткенде жүйеде қозғалыстың жаңа орнықты режимдерінің пайда болуы.
Периодтың екі еселенуі арқылы хаосқа көшу . Периодтың екі еселену құбылысы байқалса кезде, бастапқы күйде жүйе негізгі периодты қозғалыста болады. Одан кейін тәжірибенің қандай-да r параметрін өзгерткенде бифуркация, немесе, периоды алғашқысынан 2 есе артатын периодты қозғалысқа ауысу байқалады. r параметірін әрі қарай өзгерткенде, жүйе тізбекті бифуркацияларға ұшырайды, әр бифуркация кезінде период екі еселенеді. Периодтың тізбекті екі еселенуі жүретін кезде r параметрінің “күдікті” мәні п → ∞ ұмтылғанда келесі автомодельді қатынасқа бағынады:
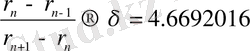 . (3)
. (3)
Бұл сан оны анықтаған адам құрметіне Фейгенбаум саны деп аталады. Іс жүзінде δ шамасы үшінші немесе төртінші бифуркацияда-ақ жинақталады. Периодтың еселену процесі белгілі бір параметрдің шекті мәнінде жиілеп, одан кейін хаосты қозғалысқа айналады.
Бифуркациялық диаграммалар. Логистикалық бейнелеудің бифуркациялық диаграммасын тұрғызу программасы және оның графигі (9-сурет) төменде келтірілген. 9-суретте келтірілген фазопараметрлік диаграмма хаосқа әкелетін периодтың екі еселену каскадты жүйесіне сәйкес. Диаграммалардың осындай түрі Фейгенбаум бұтағы деп аталады. Диаграмма динамикалық айнымалының масштабының бөлінуінің көрнекі мысалы, масштабтың скейлинг қасиеттерін көрсетеді, яғни көріністің бір элементі кішірек масштабта қайталана береді.
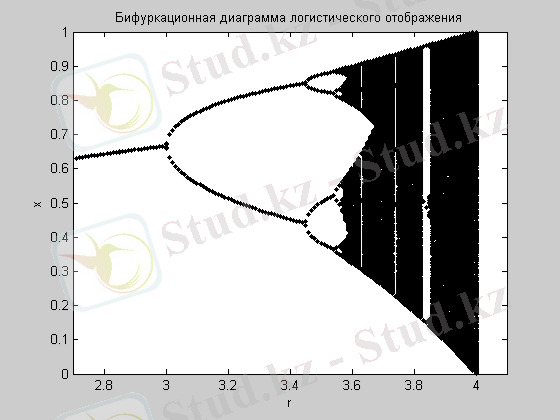
4-сурет. Логистикалық бейнелеудің бифуркациялық диаграммасы
Ляпунов көрсеткіштері ... жалғасы- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz