Периодты дискретті сигналдардың спектрі, Фурье дискретті түрлендіруі (ФДТ) және жылдам Фурье түрлендіру (ФТТ): теориясы мен Matlab-та қолданылуы


Сигналдар жыймасының спектрі
Сигналдар жыймасы радиотехникада жиі қолданылатын интегралды операция болып табылады:
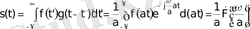
Оның Фурье түрлендіруін табайық :
 (5. 10)
(5. 10)
Алынған нәтиже өте маңызды, ол жиі іс жүзінде қолданылады: жыйманың спектрі спектрлердің көбейтіндісіне тең.
Фурьенің дискретті түрлендіруі
Дискретті периодті сигналдың спектрі қандай екендігін қарастырайық.
{ x ( k ) } санақтар тізбесі периодты болсын, оның периоды N болсын:
x ( k + N ) = x ( k ) для любого k .
Мұндай тізбекті сандардың шектелген жинағы арқылы беруге болады, бұл жинақ ретінде тізбектің ұзындығы N кезкелген үзіндісін алуға болады, мысалы { x ( k ), k= 0, 1, …, N -1}. Бұл тізбекке уақыт бойынша ығыстырылған дельта-функциялардан тұратын сигналды сәйкестендіруге болады:
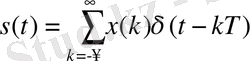 , (5. 24)
, (5. 24)
мұндағы Т - дикреттеу периоды (уақыт бойынша қадам) . Бұл сигнал да периодты болатыны, және оның минимал периоды NT -ге тең болатыны анық.
(5. 24) сигнал дискретті болғандықтан, оның спектрі периодті болу тиіс, және период 2 π / T тең болу тиіс (ол осы курста қарастырмылтайтын «Дискретті сигналдың спектрі» деген тақырыпта дәлелденеді) . Ал бұл сигнал оған қоса периодты болғандықтан, оның спектрі дискретті да болуы тиіс, және көршілес гармоникалар жиіліктерінің айырмасы 2 π /( NT ) тең болады.
Сөйтіп, периодты дискретті сигнал периодты және дискретті спектрге ие болады, бұл спектр де
N
саннан тұратын шектелген жинақпен толығымен анықталады ( өйткені спектрдің бір периодына
 гармоникалар кіреді) .
гармоникалар кіреді) .
Енді периодты дискретті сигналдың спектрін есептеуді қарастырайық. Сигнал периодты болғандықтан, оны Фурье қатарына жіктейік. Бұл қатардың коэффициенттерін жалпы (5. 4) формуласы бойынша есептейік:
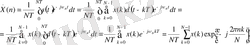 (5. 25)
(5. 25)
Сөйтіп, гармоникалардың комплексті амплитудаларын есептеудің формуласы сигнал санақтарының сызықты комбинациясы болып табылады.
(5. 25) өрнекте уақыттың нақтылы масштабы тек қосындылау операторы алдындағы 1/ Т көбейткіште білдіріледі. Дискретті тізбектерді қарастырғанда уақыттың шын масштабына байланбай, санақтар мен гармоникалардың нөмірлерін қолданады (мысалы, уақыт бойынша қадам бірінші жағдайда 0. 01 секунд болса, ал екінші жағдайда 1 минут болса, онда уақыттың 1 секунді өтті, немесе 100 минуті өтті деудің орнына, екі жағдайда да 100 санақ өтті дейді) . Сондықтан(5. 25) -тен 1/ Т көбейткішті әдетте алып тастайды, яғни дискреттеу периодын 1 тең деп есептейді. Әдетте 1/ N көбейткішті де алып тастайды (ол туралы толығырақ кішкенеден соң сөйлейміз) . Бұл өзгерістер нәтижесінде алынатын өрнек Фурьенің дискретті түрлендіруі болып табылады (ФДТ) :
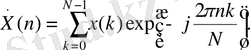 (5. 26)
(5. 26)
Кері ФДТ де бар. Дискретті спектрден сигналдың уақыттық санақтарына көшу мына формуламен жүзеге асырылады:
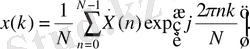 (5. 27)
(5. 27)
Бұл өрнектің тура ФДТ формуласынан айырмашылығы - экспонента дәрежесіндегі таңбасы және қосындылау оператор алдындағы 1/ N көбейткіштің бар болуы. Бұл көбейткіштің (5. 26) және (5. 27) формулалардағы орналасуы туралы мәселе әртүрлі көздерде әртүрлі шешіледі. Көздердің көбінде және копьютерлік программалардың математикалық дестелерінде (оның ішінде MatLab жүйесінде де) бұл көбейткіш кері ФДТ формуласында тұрады, бірақ кейде оны тура ФДТ формуласына қояды.
Санақтар мен спектрлік гармоникалардың нөмірлерінен уақыт пен жиіліктің шын масштабтарына көшу керек болғанда, нөмірі n гармоникаға ω= 2 πn/(NT) дөңгелектік жиілік (немесе f=n/(NT) жай жиілік) сәйкес келетінін, ал а сигналдың k - і санағына kT уақыт мезеті сәйкес келетінін еске алады.
ФДТ -і тек қана периодты дискретті сигналдың спектрін есептеу ретінде емес, ұзақтығы шектелген периодты емес сигналдың спектрін есептеу ретінде де қарастыруға болады (сигнал периоды оның ұзақтығына тең периодты сигнал ретінде қарастырылады, яғни сигнал оның ұзақтығынан тыс уақытта периодты түрде жалғасады деп есептелінеді) .
ФДТ-ң қасиеттері үздіксіз Фурье түрлендіруінің қасиеттеріне ұқсас, оның тек кейбір ерекшеліктері бар.
Жоғарыда айтылғандай, дискретті периодты сигналдың спектрі периодты болып табылады, және спектрді есептеуді
N+n >N
индекстері үшін жалғастырсақ, алынған
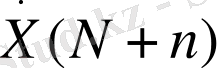 мәндер алдында алынған мәндерді толығымен қайталайды:
мәндер алдында алынған мәндерді толығымен қайталайды:
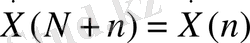 , демек мұндай сигналдың спектрі өзінің
N
санағынан тұратын тізбекпен толығымен анықталады.
, демек мұндай сигналдың спектрі өзінің
N
санағынан тұратын тізбекпен толығымен анықталады.
Котельников теоремасы бойынша, сигналды қайта тұрғызғанда бұрмалауға әкелмейтін спектрдегі ең жоғарғы жиілік Найквист жиілігіне тең:
f
N
=
f
Д
/2 = =1/(2
Т
), сондықтан бұл жиілікке сәйкес келетін гармониканың
n
нөмірі мына шарттан анықталады:
n/
(
NT
)
= 1/
2
T,
немесе
n=N
/2
.
Яғни Найквист жиілігі спектрді анықтайтын
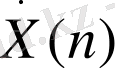 тізбектің ортасына сәйкес келеді. Онда
n>N
/2 болғандағы
тізбектің ортасына сәйкес келеді. Онда
n>N
/2 болғандағы
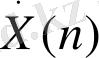 -ң мәндерінің мағынасы қандай? Нақты дискретті периодты сигналдың спектрі үшін үздіксіз нақты сигналдың спектріне тән симметрия қасиеті сақталады. Сондықтан
-ң мәндерінің мағынасы қандай? Нақты дискретті периодты сигналдың спектрі үшін үздіксіз нақты сигналдың спектріне тән симметрия қасиеті сақталады. Сондықтан
 . (5. 28)
. (5. 28)
Яғни нақты сигнал жағдайында
n>N
/2 болғандағы
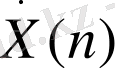 -ң мәндеріне кері жиіліктер сәйкес келеді. Сөйтіп, ФДТ -і есептеген кезде, үздіксіз түрлендіруге ұқсас, шын (нақтылы) сигналда жоқ болатын кері жиіліктер пайда болады, және екі жағдайда да олар Фурье түрлендіруінің математикалық операциясымен байланысты пайда болады.
-ң мәндеріне кері жиіліктер сәйкес келеді. Сөйтіп, ФДТ -і есептеген кезде, үздіксіз түрлендіруге ұқсас, шын (нақтылы) сигналда жоқ болатын кері жиіліктер пайда болады, және екі жағдайда да олар Фурье түрлендіруінің математикалық операциясымен байланысты пайда болады.
(5. 28) бойынша, сигналдың спектрі сақтайтын ақпарат мөлшері тап сигналдың өзі тасымалдайтын ақпарат мөлшеріндей болады: егер бастапқы тізбек (сигнал) N нақты саннан тұратын болса, онда спектр - әр қайсысы информациялық тұрғыдан екі нақты саннға сәйкес келетін N /2 комплексті саннан тұрады ((5. 28) -ден спектр N /2 қатысты «түйіндес -симметриялы болып табылатыны көрінеді, демек спектрдің екінші бөлігі мен бірінші бөлігі өзара бірмәнді түрде байланысты болып табылады, яғни спектрдің екінші жартысы жаңа (бірінші жартысынан басқа) ақпаратқа ие емес) . Ал егер сигнал нақты болмаса, онда спектр симметриялы емес болады да, уақыт аймағындағы N комплексті санаққа спектрлік аймақтағы N комплексті санақ сәйкес келеді. ных отсчетов в спектральной области.
Дискретті периодты сигналдың спектрі болып, ФДТ жиіліктердің шекьелген жолағын алатын үздіксіз периодты сигналды да оңай қайта тұрғызуға мүмкіндік береді. Бұл үшін ФДТ формуласында дискретті параметріболып табылатын k санақ нөмірінің орнына үздіксіз параметрді - t/T нормаланған уақытты (мұндағы Т - жоғарыдағыдай дискреттеу периоды) қою керек:
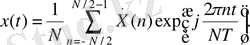 (5. 29)
(5. 29)
Қосындылау индекстерінің аралығы төмен қарай N /2 -ге ығыстырылған ( N жұп болғанда, ал N тақ болғанда қосындылау n=- ( N- 1) /2 -ден ( N- 1) /2-ге дейін жүргізіледі) . Бұл 0 -ден π/Т -ге дейінгі жиіліктер жолағын алатын аналогты сигналды алу үшін керек. Нөмірлері кері коэффициенттерді (5. 28) симметрия қатынасынан табуға болады.
ФДТ көмегімен қайта тұрғызылған үздіксіз периодты сигнал (5. 25) Котельников қатарын қолданғандағы алынатын сигналмен бірдей болады, бірақ ФДТ-і қолдану ыңғайлылау болады, өткені периодты сигнал үшін Котельников қатары қосылғыштардың шексіз сандардан, ал ФДТ - саны шектеулі қосылғыштардан тұрады.
Сандардың шектелген бірдей жинағы үшін бұл жинақ анықтайтын дискретті сигналдың спектрлік функциясын да ((5. 18) формуласы бойынша), ФДТ-ні де ((5. 26) формуласы бойынша) есептеуге болады. Сигналдың бірдей санақтарында негізделген бұл екі спектрлік көрініс бір бірімен қалай байланысты болады? Формулаларды салыстыру ФДТ дискретті сигналдың спектрлік функциясының ω n = ω Д n/N жиіліктерге сйкес келетін дискретті санақтары болып табылатынын көруге болады:
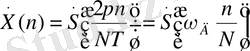 . (5. 30)
. (5. 30)
Бұл себептен ФДТ - ні кейде спектрлік санақтар деп атайды. (5. 30) қатынастан санақтардың шектелген жинағына нольдердің кейбір санын қосқанда спектрлік функция өзгермейтінін, ал ФДТ 0 ден дискреттеу жиілігіне дейінгі аралықта тығыздау орналасқан жиіліктерге сәйкес келетін спектрлік санақтардың көбірек санын беретінін көруге болады. Сөйтіп, сигналды нольдермен толықтыру ФДТ-ні есептеу кезіндегі спектрлік айыруды арттыруға мүмкіндік береді.
Фурьенің тез түрлендіруі туралы түсінік
(5. 26) формула бойынша ФДТ-ң бір коэффициентін есептеу үшін N комплекс көбейту мен қосуларды жасау керек. Сөйтіп, N коэффициентті кіргізетін барлық ФДТ-і орындау үшін N 2 «көбейту-қосу» қос операцияны жасау керек. Яғни операциялар саны ФДТ өлшемділігінің квадратына пропорционал өседі. Өте көп есептеуді жүргізудің қажет болуы Фурье түрлендіруін іс жүзінде кең қолдануға XX -і ғасырдың 60-і жылдарға дейін мүмкіндік бермеді. Ал сол жылдары бұл қиыншылықты жоққа шығарған Фурьенің тез түрлендіруінің (ФТТ) алгоритмі ұсынылды.
ФТТ-ң негізгі идеясы мынада тұрады. Егер N қарапайым сан болмаса және көбейткіштерге жікте алынса, онда талданып отырған санақтар жинағын бірнеше бөлікке бөліп алып, әрқайсы бөліктің ФТТ -н есептеп, ал одан кейін нәтижелерді біріктірсек, есептеу процесі әлдеқалай тезделеді екен. Бұл бөліктерде өз кезегінде одан ұсақ бөліктерге ажыратуға болады.
... жалғасы- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz