Сигналдарды информациялы-энтропиялық талдау жайлы

Пән: Информатика, Программалау, Мәліметтер қоры
Жұмыс түрі: Реферат
Тегін: Антиплагиат
Көлемі: 5 бет
Таңдаулыға:

СИГНАЛДАРДЫ ИНФОРМАЦИЯЛЫ-ЭНТРОПИЯЛЫҚ ТАЛДАУ

Нақтылы объектілер сыртқы ортамен энергиямен, затпен және информациямен алмаса алатын ашық жүйе болып табылады. Объектің тегіне тәуелсіз зерттелетін процес ықтималды құрылымда болса, оның симметриясы бұзылған кезде информация пайда болады. Екінші жағынан, табиғи құрылым - хаостан өз бетінше тәртіп орнау да - нақты бейсызық, ашық жүйелердің мейлінше жалпы даму заңдылығы. Информацияның және информациялық энтропияның физикалық аспектілерін қарастырайық.

Информация ұғымы

Жалпы қабылданған терминологияға сәйкес информацияның келесі анықтамаларын қолданамыз.

«Информация» ұғымы әртүрлі мағынаға ие. Қоғамдық-саяси информация әлеуметтік жүйенің өзекті жаңалықтары туралы мәліметтердің жиыны болып табылады. Кибернетикада информация ұғымы сигналдарды сақтау, өңдеу және жіберумен байланысты. Ықтималдықтар теориясында информация аддитивті мөлшерлік өлшем ретінде кездейсоқ оқиғаларды бір-біріне қатысты ықтималдылығымен салыстыру арқылы енгізіледі. Барлық информация теориясы негізінде информацияны мөлшерлі бағалау жатыр. Қарапайым комбинаторикалық формада бұл тұжырымды Р. Хартли ұсынды, ал толық аяқталған түрін К. Шеннон тұжырымдады.

Шеннон информация теориясы О және L екі таңбаның арасындағы (биттер арасындағы) қарапайым альтернативті таңдаудан шығады, ондағы L 1-ге, “иә”, “шындық” т. с. с. теңестірілсе, ал О 0-ге, “жоқ”, “жалған” теңестіріледі. Мұндай таңдау екі белгіден тұратын хабарды қабылдауға сәйкес келеді.

Мұндай хабарда болатын информация мөлшері бірлік ретінде қабылданады және ол бит деп аталады. Сондықтан бит - екілік белгі және информация мөлшерінің өлшем бірлігі, ол екі байланысқан тең ықтималдықты таңдамадағы информация мөлшері ретінде анықталады.

Айталық

(1)

- Х және Y әріптерімен сәйкес белгіленген жүйенің күйін сипаттайтын айнымалылар жыйыны болсын. Егер 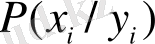- Х жүйесі 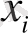күйде болғанда Y у _i күйіне өту ықтималдығы (шартты ықтималдық) болса, онда Y жүйесінің алған информациясы мынаған тең:

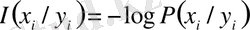. (2)

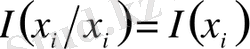- X жүйесіндегі 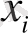оқиғасына қатысты 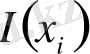информация мөлшері деп аталады.

Ықтималдық 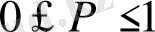арасында жатқандықтан I әрқашан оң шама.

Логарифм негізін таңдауға байланысты информация мөлшері екілік, ондық және натурал логарифм бойынша: сәйкесінше бит , дит , нат - пен өлшенеді.

Егер Х және Y жүйелерінің х _i және у _i күйлері тәуелді болмаса, онда 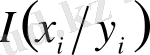= 0 Y жүйесінің у _i күйі өзінде Х- ке қатысты ешқандай информация жоқ және керісінше бұл жағдайда төмендегі теңдік орындалады:

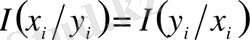Х және Y жүйелерінің х _i , y _i тәуелсіз күйлерінің бір уақытта болуының информациясы:

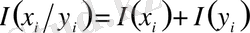. (3)

(3) -ші өрнекті информацияның аддитивтілік қасиетін көрсететін шарт ретінде енгізуге болады. (2) -ші формуладан информацияның ең маңызды универсалды мағынасы шығады: ықтималдылығы аз априорлы оқиғалар (теориялық және тәжірибеге дейінгі) информативті болып табылады. Басқаша айтқанда көп информация сирек кездейсоқ оқиғада болады. Бұл қорытынды ерекше (қайталанбайтын) оқиғаларға қолданылмайды.

Информацияны тарату жылдамдығы. Информациялық энтропия

Информацияны жеткізу байланыс арналары арқылы өтеді. Информация теориясында бұл арналардың нақты құрылғыларына көңіл бөлмей тек қана информацияны сенімді беруге болатын әртүрлі байланыс жүйелерінің информацияны жеткізу мөлшері жағынан қарастырылады.

Информацияны жеткізу жүйесін төмендегі блок-схема ретінде қарстырайық (1-сурет) . Сигналдарды тарату келесі ережелер бойынша ұйымдастырылсын:

жіберілетін сигналp(xi), i= 1. . nықтималдықпен сипатталатын статистикалық тәуелсіз сигналдардың қатары болсын;
қабылданатын сигналуксимволдарының қатары болсын;
егерn(t) шуылы болмаса, онда қабылданатын сигнал жіберлетінмен сәйкес келедіук=хi;
егер шуыл бар болса, онда берілген символ бастапқы болып қалуы (i- ші) немесе басқа (k-шы) символмен ауыстырылуы мүмкін; бұл оқиғаның шартты ықтималдығыp(yk/xi) болады;
келесі символдардың өзгерісі алдыңғы символдардың өгерісіне статистикалық тәуелді емес болсын.

1-сурет. Информацияны байланыс арнасы арқылы жеткізу жүйесінің блок схемасы

Жіберуші

Кодер

Таратқыш -модулятор

Қабылдаушы

Декодер

Қабылдағыш - демодулятор

Шуылдар, бөгеуілдер

Байланыс арнасы

n ( t )

x ( t )

I ( x, y )

y ( t ) = x ( t ) - n ( t )

Информацияны тарату жылдамдығы деп бірлік уақытта берілетін информация мөлшерін айтады. Бұл шама төмендегі формула бойынша анықталады

I (Х , У ) = S ( X ) - S ( XY ) [бит],

мұндағы энтропия бірлік уақытқа байланысты есептеледі .

Енді осы формулаға кіретін шамаларды қарастырайық. Энтропия ұғымы ашық жүйелер теориясында маңызды сипаттаманың бірі болып табылады және де статистикалық сипаттағы анықталмағандық мөлшерін, ашық жүйелердің тепе-теңсіз күйлерінің салыстырмалы дәрежедегі реттілігінің өлшемін, эволюция теориясындағы әртектілік өлшемін атқарады. Информациялық және статистикалық теорияның даму барысында энтропияның анықтамасы көптеген өзгерістерге ұшырады. Энтропия ұғымы ең алғаш термодинамикада грек тілінен аударғанда ( εντροπη ) түрлену деген мағынаны білдіретін, энергияның қайтымсыз бір бағытта таралуын анықтайтын толық дифференциал формасында енгізілген:

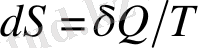, (4)

мұндағы δ Q - жүйенің қабылдайтын жылу мөлшері, Т - температура .

Энтропияның (4) -ші формула түріндегі Клаузиус анықтамасы, оның толық мағынасын ашпайды. Клаузиус энтропиясы аддитивтік тұрақтыға дейінгі дәлдікпен алынған. (4) -ші формула көмегімен энтропияны тікелей өлшеуге болмайды, себебі мұндағы температура жүйенің тепе-теңдік күйіне сай, ал жүйеге жылу берілетін жағдайда бұл шарт орындалмайды. Сол себепті (4) бойынша анықталған энтропияны өлшейтін энтропометр жоқ. Осыдан туындайтын энергияның берілу бағытына байланысты энтропияның өсуі айқын емес, соңғы кездердегі басылымдар көрсеткендей «ойландыратын тұжырым». Қорыта айтсақ, энтропияның термодинамикалық анықтамасы тепе-теңсіз құбылыстардың ерекшеліктерін ескермейді.

Статистикалық физикада энтропия ∆Г - жүйенің ішкі макроскопиялық күйінің статистикалық салмағының логарифмі ретінде енгізіледі:

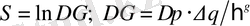, (5)

мұндағы ∆p⋅∆q- фазалық көлем, ћ -Планк тұрақтысы, g -жүйенің еркіндік дәрежесінің саны. Классикалық физикада ћ қолданбайтындықтан энтропияны нақты анықтауға болмайды. (5) -ші формуланың түрі күрделі жүйенің энтропиясының аддитивтік талаптарынан шығады:

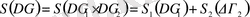. (6)

Идеал газдың энтропиясын (4) -ші формула бойынша есептей отырып (5) -ші формулаға келуге болады, мұндағы ∆Γ - идеал газдың қысымы, көлемі, температурасы бойынша анықталады.

Энтропия түсінігі сонымен қатар кездейсоқ шамалардың ықтималдықтарының таралуына да байланысты. Е _i энергияның теңықтималдықты таралуы кезінде жүйенің ішкі таралу ықтималдылығы былай анықталады.

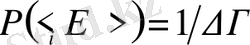Энтропияны мына түрде табамыз

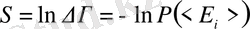. (7)

Орташа ықтималдықтың мағынасы бойынша (7) былай жазылады:

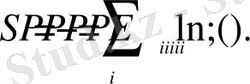(8)

(8) - бойынша анықталған энтропия информациялық энтропия деп аталады. (2) және (8) өрнектерін салыстыру арқылы информациялық энтропия информацияның орташа ықтималдық мәнін анықтайтындығы көрінеді. Жүйенің теңықтималды таралуы кезінде жүйе туралы анықталмағандық максимумге жетеді, яғни жүйе туралы барлық информация жоғалып энтропияға айналады (7) . Тепе-тең жүйе информацияны сақтай алмайды. Информацияны білу анықталмағандықты азайтады. Сондықтан информация мөлшерін жоғалған анықталмағандық, яғни энтропия мөлшерімен өлшеуге болады:

I = S _pr - S _ps ,

... жалғасы

Сіз бұл жұмысты біздің қосымшамыз арқылы толығымен тегін көре аласыз.