Сигналдардың мультифракталдық талдауы: Dq өлшемдері мен f(α) спектрінің теориялық негіздері


Жұмыс түрі: Реферат
Тегін: Антиплагиат
Көлемі: 7 бет
Таңдаулыға:
2. 1. Сигналдардың мультифракталдық талдауы
Бұл бөлімде біз мультифрактал теориясының негізін қарастырымыз. Мультифрактал біртекті емес фракталды обьектілерден құралған [6] . Оны сипаттау үшін регулярлы фракталдармен салыстырғанда бір ғана мөлшер - фракталдың өлшемділігі D, енгізу жеткіліксіз, яғни сан жағынан шексіз өлшемділіктер енгізу қажет. Бұның себебі, D мөлшермен анықталатын таза геометриялық сипаттамалармен қатар, бұл фракталдар кейбір статистикалық қасиеттерге ие. «Біртекті емес» сөзінің мағынасын көптік нүктелерінің фрактал бойынша біркелкі емес таралуы деп түсіну керек. Біртектіліктің болмау себебі, фракталдың геометриялық бірдей әртүрлі ықтималдылықпен толтырылуында, немесе, сәйкес аудандарды геометриялық өлшемдерге толтыру ықтималдылықтарының сәйкес келмеуі.
d (d = 1 - сызық, d = 2 - жазықтық, d = 3 - үш өлшемді кеңістік) өлшемділігі бар Евклидтік кеңістікте өлшемі L болатын, ℒ шектеулі ауданды алатын фракталды обьектіні қарастырайық. Фракталды объектінің құрылуның белгілі бір сатысында ол осы ауданда таралған, N >> 1 нүктелерден құрылған көптік болсын, түбінде N →
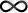 болады деп есептейміз. Барлық ℒ ауданды δ жақты және δ
d
көлемді кубтық аудандарға бөлейік. δ-ның азаюына байланысты ауданды алып жатқан ұяшықтардың саны N(δ), мына дәрежелік заңға байланысты өзгеріп отырады:
болады деп есептейміз. Барлық ℒ ауданды δ жақты және δ
d
көлемді кубтық аудандарға бөлейік. δ-ның азаюына байланысты ауданды алып жатқан ұяшықтардың саны N(δ), мына дәрежелік заңға байланысты өзгеріп отырады:
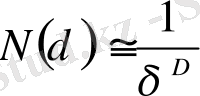 , (2. 1. 1)
, (2. 1. 1)
D хаусдорфты немесе фракталды өлшемділік. (1) қатынасын логарифмдейік және δ-ны нoльге ұмтылдырып, мынаны жазуға болады:
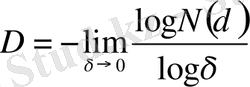 . (2. 1. 2)
. (2. 1. 2)
Логарифмді кез-келген оң негіз немесе бірден өзге негіз арқылы алуға болады, мысалы, негізі 10 немесе
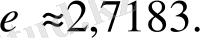 D фракталды өлшемділіктің ортақ анықтамасы болып табылады. Осыған сәйкес D- нің мәні берілген обьектінің өзіндік сипаттамасы болып табылады [6] .
D фракталды өлшемділіктің ортақ анықтамасы болып табылады. Осыған сәйкес D- нің мәні берілген обьектінің өзіндік сипаттамасы болып табылады [6] .
Көп өлшемді объектілердің фракталды өлшемділіктері. Бір өлшемді фракталды объектілердің өзұқсас қасиетке ие немесе масштабтық инварианттылығы болады, яғни, кіші бөлшектер үлкенге ұқсас. Егер анықтайтын айнымалылардың саны бірден үлкен болса және осы айнымалылар бойынша ұқсастық коэффициенттері әр түрлі болса, онда бұндай фракталдық объектілер өзаффинді деп аталады. Өзұқсас фракталдарға мысал ретінде, біртекті ортада қозғалатын, броундық бөлшектердің траекториясын алуға болады. Бұл жағдайда координаттар осі біркелкі, ұқсастық коэффициенттері барлық бағытта бірдей. Және осы уақытта бөлшектің координатасының уақытқа тәуелділігі өзаффиндік фракталды қисықты береді, бөлшектің қозғалуы уақытқа сызық бойымен тәуелді болғандықтан, коэфиценттері, координат және уақыты бойынша әртүрлі болып келеді. Өзаффинді фрактал ретінде күрделі генераторлардан алынған сигналдардың және жартылай өткізгіш жұқа пленкалардың уақыттық және кеңістіктік энергетикалық спектрлердің т. б. қисық пішіндерін қарастыруға болады.
Б. Мандельброт модельді фракталдар үшін аффиндік көрсеткіштерді енгізді. Олар арқылы фракталдық өлшемдер анықталады және олардың Херстің эмпирикалық көрсеткіштерімен байланысы болуы мүмкіндігін көрсетеді. Алайда реалды жағдайда белгілі бір сәйкес масштаб (аффиндіктің көрсеткішін анықтайтын) әлі анықталмаған. Белгілі болып табылатын периметрі мен ауданының қатынасы тек қана эмпирикалық тұрақтылық арқылы фракталдық өлшемділігінің тек бір ғана мағынасын анықтайды, онысы - ең бір көп салалы емесі болып табылады. Хаусдорф формуласы (2), фракталды өлшемділікті зерттейтін басқа да әдістер өзаффинді обьектілерді зерттеуде олардың фракталдану заңдылығын білмей қолданысқа түсе алмайды. Төменірек өзаффиндік обьектілердің фракталдық өлшемділігін бос параметрлерсіз анықтау әдісін қарастырып, нәтижесін инерциялық сызықсыздығы бар генератор белгілерін сипаттауға қолданамыз [6] .
Фракталды өлшемдер - ұзындық L(δ), аудан F(δ), көлем V(δ) әдетте өлшемнің ортақ формуласымен анықталады, кез келген аддитивті өлшенетін физикалық шама M (масса аналогы) :
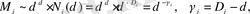
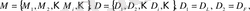 (2. 1. 3)
(2. 1. 3)
бұл жерде N(δ) - ұяшықтардың ең аз саны, олар жиын элементтерін сипаттау үшін жеткілікті болып табылады.
D- ның массасын M арқылы табудың кері тапсырмасын қоюға болады, егер оларды фракталдар үшін интервал мен интегралдуының нүктелерінің шашырауының санын яғни δ-ға тәуелді интегралдар ретінде алсақ. Кездейсоқ түрде δ-ның мағынасын немесе δ-өлшемді ұяшық номерін таңдай отырып, біз бір әдіспен тұрақты және кездейсоқ фракталдарды қарастыруымызға болады.
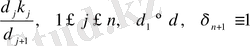 , (2. 1. 4)
, (2. 1. 4)
Енді фракталдық өлшемділіктің ортақ формуласымен жазайық
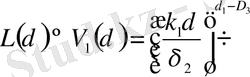 ,
,
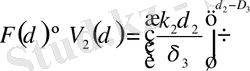 ,
,
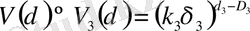 , (2. 1. 5)
, (2. 1. 5)
бұл жерде - d 1 = 1, d 2 = 2, d 3 = 3 - ұзындықтың ауданның, көлемнің топологиялық өлшемдері. (V) - тен δ 2 мен δ 3 - ті алып тастасақ
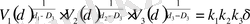 . (2. 1. 6)
. (2. 1. 6)
n-өлшемді жағдайда
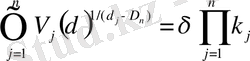 , (2. 1. 7)
, (2. 1. 7)
мұндағы V j (δ) - көп өлшемді фракталды өлшем, D n - оның фракталды өлшемділігі. Егер фракталды өлшемдер сызықтың деформациясынан, үстінен, топологиялық өлшемдердің d i , i = 1, 2, 3 көлемінен түзілетінін еске алсақ, ортақ жағдайда мынаны қабылдауға болады
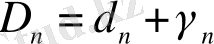
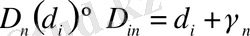 ,
,
 , (2. 1. 8)
, (2. 1. 8)
мұндағы γ n - скейлинг көрсеткіші, яғни D n -нің бөлшек бөлігі.
D n - анықталатын (19) мағынасы n-сатысының сызықсыз теңдеуі болып табылады. (19) -дегі V j көрсеткіштерінің тең болған жағдайында, яғни
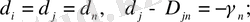
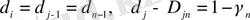 (2. 1. 9)
(2. 1. 9)
біз γ n -ге қатынасты теңдеуге ие боламыз [6] .
(9) -дың талабы D n -өлшемділікті n-өлшемді обьектінің d n және d n-1 топологиялық өлшемділікті элементтердің каскадты деформациясы нәтижесі жолымен түзілуін білдіреді. Мысалы үшін d n-1 арқылы өтетін фракталдануы n = 1 болғанда көптеген нүктелерден тұратын фракталды қисық көрінетін. n = 3 болғанда үстіңгі жақтың деформациясы нәтижесінде түзілетін, нүктелерден құралған қисықтан тұратын фракталды обьектінің байқалатынын білдіреді.
Фракталдық өлшемдіктері арқылы өзаффиндік жиындардың жалпылама суреттеу мүмкіндігін көрсеттік. Осы бөлімнің негізгі теңдігі болып, көпөлшемді факталды өлшем арқылы анықталатын фракталдық өлшемдер, күрделі геометриялық обьектілердің форма коэффициенттері және өзаффинді фракталдар ретінің параметрлерінің кірістіру мүмкіндігін орнату болып табылады. Өлшеу масштабы кішірейсе, реттің жергілікті параметрі өседі, ал жалпылама параметрі өлшеу масштабы көбейсе өседі. Үздіксіз фракталдық қисықтың симметриясының өзгеруі екінші текті фазалық ауысуға ұқсас [6] .
Евклидтік кеңістіктегі L өлшемі бар фракталдық обьектіні қарастыруға қайтып келсек. Біз ең кемінде бір нүктесі бар ұяшықтарды қарастырайық. Ұяшықтардың нөмері i мына түрде өзгерсін i = 1, 2, . . . N(δ), N(δ) -δ ұяшық өлшеміне тәуелді ұяшықтардың суммалық саны. Егер нүктелердің ұяшықтар бойынша таралуы біркелкі болмаса, фрактал біртекті емес, яғни мультифрактал болып табылады. Мультифракталды суреттеу үшін, ℒ аудандағы нүктелердің таралуын сипаттайтын, жалпылама фракталдық өлшемділіктер жиыны енгізіледі.
n i (δ) - i нөмерге ие ұяшықтағы нүктелер санын берсін, онда
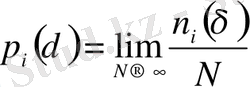 (2. 1. 10)
(2. 1. 10)
p i (δ) шамасы кездейсоқ алынған нүктенің i ұяшығында болу ықтималдылығы. Жалпылама фракталдық өлшемділіктердің спектрі D q мына қатынаспен анықталады:
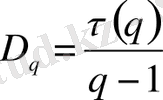 , (2. 1. 11)
, (2. 1. 11)
q -
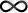 < q +<
< q +<
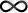 аралығындағы кез-келген мәнді қабылдайды,
аралығындағы кез-келген мәнді қабылдайды,
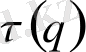 функциясы мына түрге келеді:
функциясы мына түрге келеді:
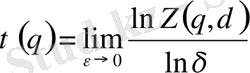 , (2. 1. 12)
, (2. 1. 12)
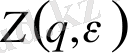 - жалпылама статистикалық сумма:
- жалпылама статистикалық сумма:
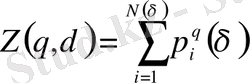 . (2. 1. 13)
. (2. 1. 13)
Егер D q = D = const, яғни q-дан тәуелсіз, онда берілген нүктелер жиыны фракталдық өлшемділікпен ғана сипатталатын жәй, регулярлы фракталды береді. Егер D q q-ға байланысты өзгерсе, онда берілген нүктелер жиыны мультифрактал деп саналады. .
Жалпы түрде мультифрактал белгілі - бір бейсызық функциясымен
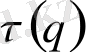 сипатталады. Нүктелердің таралу сипатын білу үшін
сипатталады. Нүктелердің таралу сипатын білу үшін
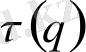 функциясының туындысы да қажет:
функциясының туындысы да қажет:
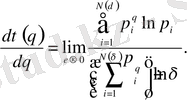 (2. 1. 14)
(2. 1. 14)
q = 1 болса, жалпылама фракталдық өлшемділік мынаған тең:
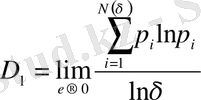 . (2. 1. 15)
. (2. 1. 15)
Бұл формуладағы бөлімі фракталдық жиынның энтропиясын береді. Нәтижесінде жалпылама фракталдық өлшемділіктің D 1 пен энтропияның S(δ) байланысы мынандай:
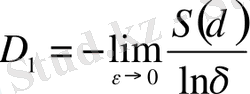 . (2. 1. 16)
. (2. 1. 16)
бұдан,
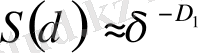 , (2. 1. 17)
, (2. 1. 17)
яғни, D 1 белгілі-бір ұяшықтағы нүктенің орнын анықтауға керек информацияны сипаттайды. Осыған байланысты жалпылама фракталдық өлшемділікті D 1 информациялық өлшемділік деп те атайды [6] .
Мультифракталдық спектрдің функциясы - f(α)
D q шамалары шын мәнінде фракталдық өлшемділік болып табылмайды [6] . Сондықтан, олармен қатар мультифракталды жиынды сипаттау үшін М. спектрдің функциясын f(α) қолданылады (Мультифрактал сингулярлығының спектрі) . f(α) шамасы берілген q шамасындағы статистикалық суммаға үлес қосатын ℒ көптіктің біртекті фракталдық бөлігінің, өзі тектес көптіктерге р i -дің δ ұяшық өлшемінен тәуелділігі дәрежелік сипат береді :
 (2. 1. 18)
(2. 1. 18)
бұндағы α i - дәреженің белгілі бір көрсеткіші (әртүрлі ұяшыққа әртүрлі I алынады) . біртекті фрактал үшін α i дәрежесінің барлық көрсеткіштері бірдей және D мөлшеріне тең.
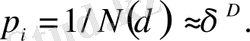 (2. 1. 19)
(2. 1. 19)
Бұл жағдайда статистикалық сумма мынадай болады.
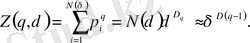 (2. 1. 20)
(2. 1. 20)
- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz