Сигналдардың энергиясы мен қуаты және корреляциялық талдаудың негіздері


СИГНАЛДЫҢ ЭНЕРГИЯСЫ МЕН ҚУАТЫ
Сигналдың энергиясы мен қуаты - сигналдың іс жүзінде жиі қолданатын, өте маңызды сандық сипаттамаларының бірі. Олардың сигналдар теориясындағы анықтамалары әдетте қолданылатындардан өзгеше болып табылады.
Энергия мен қуаттың әдеттегі, «физикалық» ұғымдарын қарастырайық. Егер кедергісі
R
тең резисторға тұрақты
U
кернеу түсірілген болса, резисторда бөлінетін қуат
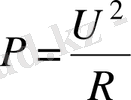 тең болады.
Т
уақыт ішінде бұл резисторда
тең болады.
Т
уақыт ішінде бұл резисторда
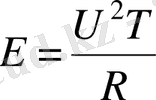 тең жылулық энергия шығарылады.
тең жылулық энергия шығарылады.
Енді бұл резисторға тұрақты емес, айнымалы кернеу, яғни
s(t)
сигнал, түсірілген болсын. Онда резисторда шашыралатын қуат та уақытқа тәуелді болады, яғни бұл жағдайда
лездік
қуат (instantaneous power) туралы айту керек:
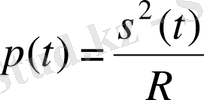 .
.
Т
уақыт ішінде бөлінетін энергияны есептеу үшін, лездік қуатты бұл уақыт аралығы бойынша интегралдау керек:
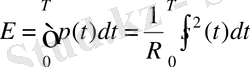 .
.
Энергияны ол шығарылған уақыт аралығына бөліп, сол уақыт аралығындағы
орташа
қуат (average power) деген ұғымды енгізуге болады:
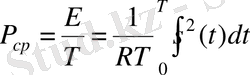 .
.
Барлық келтірілген формулаларға жүктеменің R кедергісі кіреді . Бірақ, энергия мен қуат бізді физикалық шамалары ретінде емес, әртүрлі сигналдарды салыстырудың құралы ретінде қызықтырса, бұл параметрді формулалардан шығарып тастауға болады ( R = 1 деп есептеуге болады) . Сөйтіп біз сигналдар теориясында қабылданған энергияның, лездік қуаттың және орташа қуаттың анықтамаларын аламыз:
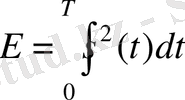 ,
,
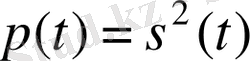 ,
,
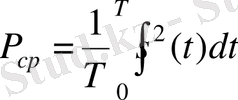 . (1)
. (1)
Мұндағы «қуаттың» өлшемділігі - В 2 , ал «энергияның» өлшемділігі - В 2 ⋅ с.
Кедергінің мәні бірге тең деп алынғанына назар аудару үшін, бұл параметрлерді кейде меншікті қуат пен энергия деп атайды.
Сигнал энергиясы шексіз және шектелген болуы мүмкін. Мысалы, ұзақтығы шектелген кез-келген сигналдың энергиясы да шектелген болады (егер сигналда дельта-функциялар мен шексіздікке кететін тармақтары болмаса) . Ал кез-келген периодты сигналдың энергиясы шексіз болады.
Егер сигналдың энергиясы шексіз болса, оның барлық уақыт осіндегі орташа қуатын анықтауға болады. Бұл үшін (1) формуладағы орташалау аралығын шексіздікке ұмтылдырып, шекті ауысуды жасау керек:
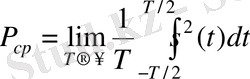 . (2)
. (2)
Орташа қуаттың квадраттық түбірі сигналдың орташа квадраттық (әрекеттегі) мәнін (root mean square, RMS) береді:
 . (3)
. (3)
Периоды Т тең периодты сигнал үшін (2) мен (3) формулалардағы шекті ауысуды жасау міндетті емес - период бойынша орташалауды орындау жеткілікті болады.
СИГНАЛДАРДЫҢ КОРРЕЛЯЦИЯЛЫҚ ТАЛДАУЫ
Корреляциялық таладаудың мағынасы - сигналдардың бiр бiрiне ұқсастығын сандық түрде өлшеу. Бұл үшiн корреляцилық д. а. функциялар қарастырылады. Олардың екі түрi бар.
Өзара корреляцияның функциясы
2 энергиясы шектелген детерминдi сигналдың ӨКФ-сы осы сигналдар көбейтiсiнi шексiз шектерде алынатын интеграл б. т. (сигналдардың бiреу τ уақытқа кiдiртiлген болады)
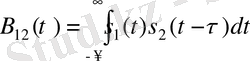 (1)
(1)
Ол бiр сигнал екiншi сигналға қатысты кешiгу мүмкiн екендiгiн еске алып, сол екi сигналдың ұқсастық дәрежесiн өлшеуге мүмкiндiк бередi - неғұрлым ӨКФ көп болса, соғұрлым бұл ұқсастық көп болады.
ӨКФ қасиеттерi мынадай:
1.
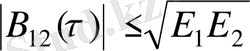 ,
мұнда
E
1
мен
E
2
- s
1
(t)
мен
s
2
(t)
сигналдар энергиялары
.
,
мұнда
E
1
мен
E
2
- s
1
(t)
мен
s
2
(t)
сигналдар энергиялары
.
- , яғниτ-ң белгiсiн өзгерту сигналдарды орындарымен ауыстырғандай болады.
- ӨКФ-ң максимумыτөсiнiң кезкелген жерiнде болуы мүмкiн, τ= 0 болғанадағы мәнi ешнәрсемен (ешбiр затпен) бөлiнбейдi.
- Энергиясы шектелген сигналдардың ӨКФ -іτсуімен өшеді;
- Егер сигналдарда дельта-функция түрiндегi ерекшелiктерi болмаса, олардың ӨКФ-те үзiлiстер бола алмайды.
- Сигналдар - кернеу болса, олардың ӨКФ-ң өлшемділігі В2· с болады.
Шындықта (нақтылықта) ұзақтығы шексiз сигналдар мүмкiн емес, сондықтын iс жүзiнде (1) интеграл стгналдар ұзақтығымен не КФ есептеудiң керектi дәлдiгiмен анықталатын шектерде алынады (егер ол бойынша интеграл алынатын интервал өте қысқа болса, онда бұл интервалдағы сигналдың үзiндiсi тасымалдайтын ақпарат КФ керектi дәлдiкпен есептеу үшiн жеткiлiксiз болуы мүмкiн) .
Сигналдар ұзақтығының КФ-ға әсерiн алып тастау үшiн, оны жиiитервал ұзындығына нормалайды (мөлшерлейдi) :
, или (2)
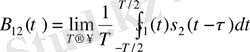
Мұндай тәсiлмен есептеуде 1) және 6) қасиеттер өзгередi.
Периодты сигналдар үшiн ӨКФ ұғымы әдетте енгiзiлмейдi, бiрақ та сигналдар периоды бiрдей болса оны енгiзуге болады. Сигналдар периодты болғанда (1) интеграл шексiз болатындықтан, ӨКФ-тi бұл жағдайда жылжытылған үлгiлер көбейтiндiсiн бiр период шегiнде орташалап есептейдi:
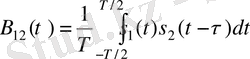
ӨКФ көмегiмен, мысалы, екi сигналдың бiр бiрiне қатысты кешiгуiн анықтауға болады: ол ӨКФ максимал болған τ мәнiне тең болады.
Дискретті f(t) пен g(t) сигналдар үшін
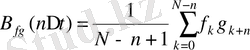
Корреляциялық функция
Энергиясы шектелген детерминдi сигналдың корр., немесе автокорр. функциясы сигнал мен оның жылжытылған үлгiсi арасындағы ұқсастығы дәрежесiн көрсетедi. Ол бiр сигналдың екi, бiр бiрiне қатысты τ уақытқа жылжытылған, үлгiсiнiң көбейтiсiнен интеграл б. т. :
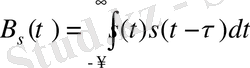
КФ екi сигнал бiрдей болғандағы ӨКФ-ң жеке жағдайы болып табылатыны анық. КФ-ң қасиеттерi ӨКФ-тен сәл басқаша болады:
1.
τ
= 0 болғанадағы КФ мәнi сигналдың энергиясына тең болады
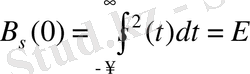 .
.
2. КФ
τ
аргументінің жұп функциясы б. т. :
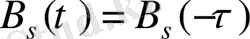
- τ= 0 болғандағы КФ-ң мәнi мүмкiндi мәндер iшiнен ен жоғары (максимал) б. т. :
- Энергиясы шектелген сигналдың КФ -іτсуімен өшеді;
- Егер сигналда дельта-функция түрiндегi ерекшелiктерi болмаса, оның КФ-те үзiлiстер бола алмайды.
- Сигнал кернеу болса, оның КФ-ң өлшемділігі В2· с болады.
Энергия шексiз сигнал, мысалы периодты сигнал жағдайында, келтiрiлген анықтаманы қолдануға болмайды. Сондықтан периоды Т сигналдың КФ-н жылжытылған үлгiлердiң көбейтiсiн бiр период шегiнде орташалап есептейдi:
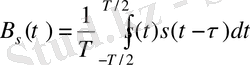
Мұндай КФ-ң қасиеттерi сәл өзгередi:
1. τ = 0 болғанадағы КФ мәнi сигналдың орташа қуатына тең болады
2, 3, 5 қасиеттер сақталады
4. Периодты сигналдың КФ-ы периоды сигналдың периодына тең периодты функция б. т.
... жалғасы- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz