Өзаффинді және өзұқсастық статистикалық жүйелердің информациялық-энтропиялық критерийлері


Теңсіздік статистикалық жүйенің өзаффинді және өзұқсастығының информация-энтропиялы критерилері
Информация түсінігі кибернетикада, генетикада, социологияда кеңінен қолданылады. Синергетика және ашық жүйелер физикасының дамуы ғылымның әртүрлі салаларында пайдалану үшін жарамды информацияларды универсалды анықтауды талап етеді. Ашық жүйенің өзінің анықтамасы информация түсінігін құрайды: ашық жүйе деп сыртқы ортамен заттарымен, энергиямен, информациямен алмасатын жүйе аталады [14] .
Әдетте күрделі түсінік анықтамасы оның негізгі қасиеттерінің тізімі арқылы құрылады. Кейбір физикалық шамасының статистикалық реализациясының информациясы оң шама болып табылады және , егер теңсіздігі бар кезде анықталады. Егер шамасының пайда болу ықтималдығы болса, онда информация саны үшін өрнек:
(2. 1)
осы қасиеттерді бейнелейді. Процестің шартымен ескеріледі. Әртүрлі ғылымдар тұрғысынан информацияның көптеген анықтамасы ұсынылған. (2. 1) формуласы осы барлық анықтамамен үйлесімді.
кейбір шарттары бар кезде информацияны шартсыз және шартты энтропияның айырымы арқылы анықтайды:
. (2. 2)
Бұл формула техникалық тапсырмалар үшін қолданылады, мысалы, байланыс каналдарының өткізетін қабілетін бағалау үшін қолданылады. Алайда, энтропияның өзінің информациясы информацияның орташа мәні болып табылады:
, (2. 3)
мұндағы - көптеген мәндерін ұяшықтағы нөмірі. Сондықтан (2. 1) формуласын информацияның негізгі анықтамасы ретінде қабылдаймыз.
Осылайша, информацияның универсалды анықтамасы болмаса да ол әртүрлі табиғаттағы құбылыстарды бейнелеу үшін қолданылады. Сондықтан информациялық құбылыстар теориясында басқа жаңа амал қолданылуы мүмкін. Белгілі бір тәуелсіз айнымалы ретінде информацияның өзін қабылдауға болады. Процестің статистикалық сипаттамасын информация арқылы өрнектей отырып, информацияның жаңа қасиеттерін іздеуге болады, мысалы, масштабты-инвариантты қасиеттер.
Осыдан кейін информацияны жүзеге асыру ықтималдығы туралы (52) формулаға сәйкес айтуға болады:
. (2. 4)
ықтималдық тығыздығы үшін мына формулаларға ие боламыз:
. (2. 5)
информацияны жүзеге асыру ықтималдығының функциясы ықтималдық тығыздығының таралу функциясына сәйкес келеді. Дәл (2. 1) формуламен анықталған информация масштабты инварианттылыққа ие: бөлігі мен бүтіні бірдей таралу заңдылыққа ие. информация мәнінің таралуының информациялық энтропиясын информацияның орташа мәні ретінде анықтаймыз:
, (2. 6)
үшін ие боламыз, яғни энтропия бірге нормаланған. Үздіксіз көптеген энтропия айнымалылардың секірмелі түрде өзгеруі кезінде шексіз және сондықтан интеграл Лебег мағынасында кейбір өлшемдерді енгізу жолымен анықталады. Өлшемдер ретінде информацияның өзін алып және нәтижелерге қол жеткіздік (2. 6) .
Белгілі функционалдық теңдеуді пайдаланайық, оны сипатты функция мына масштабты - инвариантты қасиетпен қанағаттандырады:
, (2. 7)
мұндағы - масштабты көбейткіш. Кез-келген үздіксіз функция өзінің қозғалмайтын нүктесінде (2. 6) теңдеуін қанағаттандырады. Сипатты функция ретінде және функцияларын қабылдап, олардың қозғалмайтын нүктелерін анықтайық:
, (2. 8)
. (2. 9)
Бұл қозғалмайтын нүктелер жалғыз берік нүктелер болып табылады, өйткені олар сондай-ақ кез-келген бастапқы мәндерінде алынатын есепсіз бейнелеудің шегі болып табылады:
(2. 10)
(2. 11)
мұндағы жақшалар тең.
, сандарының физикалық мағынасының әртүрлі түсініктері мүмкін. Ықтималдық тығыздығы локалды сипаттама болып табылады, сондықтан ол әртүрлі айнымалы бойынша өзгеше болуы мүмкін және санын өзаффинділік критериі ретінде қабылдауға болады. Энтропия - орташаланған сипаттама, сондықтан саны өзұқсастық критериі болып табылады.
Басқа жағынан, сандары сәйкесінше, статистикалық өзұқсастық және өзаффиндік жүйелер үшін Фиббоначи санының (динамикалық өлшемнің “алтын қимасы”) аналогы ретінде қарастырылуы мүмкін. Шынында, (59) формуласынан кезінде мынаған ие боламыз
, (2. 12)
сондай-ақ кезінде (2. 8) - ден аламыз. Біз өзаффиндік, динамикалық тепе-теңдік, өзұқсастықтың ұқсас заңдылықтары бір формуламен (59) бейнеленетінін көрдік.
2. 9 Ашық жүйелер эволюциясының әмбебап энтропиялық заңдылықтары
Ашық жүйелер физикасында өзұқсас және өзаффиндік режімдерді пайдаланумен байланысты мәселелер маңызды болып табылады. Егер айнымалыларды анықтайтын сан бірліктен көп болса және осы айнымалылар бойынша ұқсас коэфиценттер түрліше болса, фракталды объект өзафиндік болып табылады. Егер фракталды объектінің иерархиялық бөліктері барлық айнымалылар бойынша бірдей ұқсас коэффиценттерге ие болса, объект өзұқсас деп аталады. З. Ж. Жаңабаевтың [15] жұмысында информация мен энтропияны жүзеге асыру ықтималдылығы тығыздығының жылжымайтын нүктелер түріндегі (
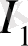 ) өзаффинділік пен (
) өзаффинділік пен (
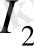 ) өзұқсастың информациялық-энтропиялық критерийлері анықталды:
) өзұқсастың информациялық-энтропиялық критерийлері анықталды:
,
;
,
. (2. 13)
Соңғы жылдары жаңа жалпылама статистикалық механика дамып келеді, оны Цаллис статистикасы деп немесе Гиббстың жалған канондық статистикасы деп атауға болады [17] . Осындай теориялардың негізін келесі түрдегі экспоненциалды функцияны пайдалану құрайды:
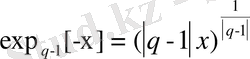 (2. 14)
(2. 14)
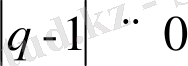 шегінде біз Гиббс канондық үлестіруін сипаттайтын кәдімгі
шегінде біз Гиббс канондық үлестіруін сипаттайтын кәдімгі
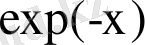 функциясын аламыз.
функциясын аламыз.
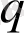 параметрі бірлігінен айырмашылығы, жүйенің статистикалық теңсіздігін, біртекті еместігін сипаттайды. Оңайлау болу үшін біз бұдан әрі
параметрі бірлігінен айырмашылығы, жүйенің статистикалық теңсіздігін, біртекті еместігін сипаттайды. Оңайлау болу үшін біз бұдан әрі
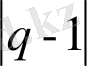 орнына
орнына
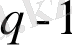 мәнін пайдаланамыз, қажет болған жағдайда ізделінетін физикалық шаманың оң белгісін таңдаймыз.
мәнін пайдаланамыз, қажет болған жағдайда ізделінетін физикалық шаманың оң белгісін таңдаймыз.
(2. 14) мәнін пайдалана отырып,
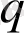 информациялық энтропиядан - тепе-тең емес жүйенің күрделігінің, белгісіздігінің бірден-бір шарасына тәуелділікті анықтаймыз.
информациялық энтропиядан - тепе-тең емес жүйенің күрделігінің, белгісіздігінің бірден-бір шарасына тәуелділікті анықтаймыз.
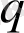 параметрімен сипатталатын жалған үдеріс үшін, информацияны келесі түрде анықтаймыз:
параметрімен сипатталатын жалған үдеріс үшін, информацияны келесі түрде анықтаймыз:
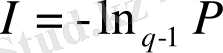 . (2. 15)
. (2. 15)
Осыдан келіп ықтималдылықты информация функциясы ретінде көрсетеміз:
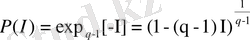 . (2. 16)
. (2. 16)
Информацияны жүзеге асыру ықтималдығы үлестіруінің тығыздық функциясы
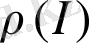 былай анықталады:
былай анықталады:
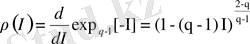 . (2. 17)
. (2. 17)
Энтропия информацияның орташа мәні ретінде анықталады:
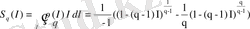 . (2. 18)
. (2. 18)
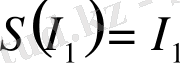 және
және
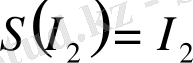 өзұқсас мәндерін жылжымайтын көрініс нүктелері ретінде табамыз:
өзұқсас мәндерін жылжымайтын көрініс нүктелері ретінде табамыз:
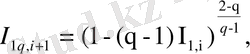 (2. 19)
(2. 19)
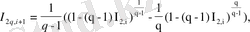 (2. 20)
(2. 20)
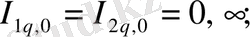
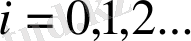 .
.
Сөйтіп,
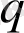 параметрі информация және информациялық энтропия мәндері арқылы өзұқсас және өзаффиндік күйінен ауытқуын сипаттай алады.
параметрі информация және информациялық энтропия мәндері арқылы өзұқсас және өзаффиндік күйінен ауытқуын сипаттай алады.
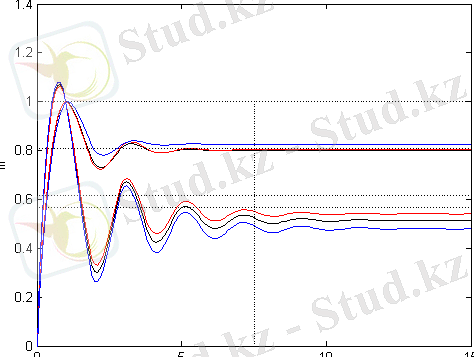
2. 1 сурет - Информация - энтропиялық диаграмма
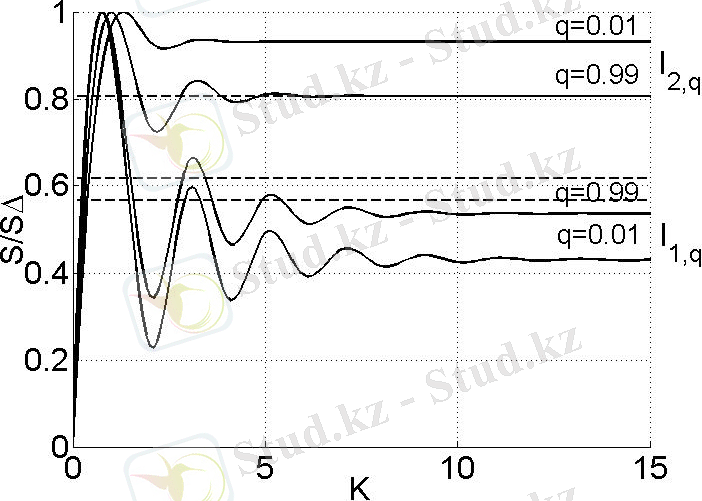
2. 2 сурет - Жүйенің жалпылама метрикалық сипаттамаларының өзгерісі кезіндегі энтропияның өзгерісі.
III
II
IV
V
i *
0. 567
0. 806
0. 618
I
i
S
Процестер:
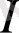 − шуылтәрізді,
− шуылтәрізді,
 − өзұқсас,
− өзұқсас,
 − өзаффинді,
− өзаффинді,
 − біртексіз,
− біртексіз,
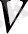 − өзқауымдық.
− өзқауымдық.
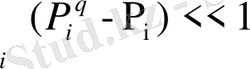 , (2. 21)
, (2. 21)
Шарты жағдайында (1. 30) формуласымен анықталатын Реньи энтропиясымен сәйкес келеді:
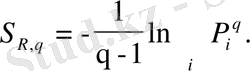 (2. 22)
(2. 22)
Біртекті еместік параметрін формуласымен анықтауға болады:
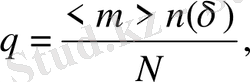 (2. 23)
(2. 23)
мұнда
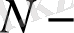 нүктелердің (есептеулердің) жалпы саны,
нүктелердің (есептеулердің) жалпы саны,
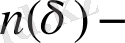
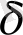 өлшеу масштабы бар,
өлшеу масштабы бар,
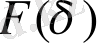 ауданын жауып тұратын,
ауданын жауып тұратын,
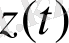 қисықтарымен шектелген ұяшықтардың минималды саны,
қисықтарымен шектелген ұяшықтардың минималды саны,
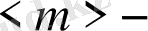 ұяшықтағы нүктелердің орташа саны. Оңай болуы үшін
ұяшықтағы нүктелердің орташа саны. Оңай болуы үшін
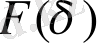 -ны жергілікті максимумдарды біріктіретін тік сызықтармен шектелген z(t) және
-ны жергілікті максимумдарды біріктіретін тік сызықтармен шектелген z(t) және
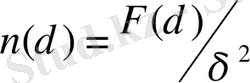 фигура ретінде қарастыруға болады.
фигура ретінде қарастыруға болады.
Біртекті еместік параметрін Риман интегралын Лебег интегралына қатынасы арқылы есептеуге болады:
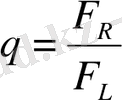 , (2. 24)
, (2. 24)
мұнда
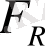 - Риман бойынша
- Риман бойынша
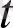 бойынша
бойынша
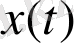 сигналының интегралы,
сигналының интегралы,
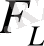 - Лебег интегралы.
- Лебег интегралы.
Егер зерттелініп отырған үдеріс тұрақты
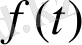 және кездейсоқ
және кездейсоқ
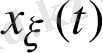 функциялардың туындылары түрінде берілсе, онда Риман интегралы былай жазылады:
функциялардың туындылары түрінде берілсе, онда Риман интегралы былай жазылады:
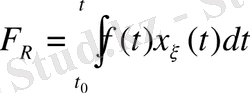 . (2. 25)
. (2. 25)
Риманның әдісі бойынша уақыттық өс тең аралықтарға
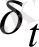 бөлініп,
бөлініп,
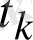 мәндеріне сәйкес, функция мәндерін табады, мұнда
мәндеріне сәйкес, функция мәндерін табады, мұнда
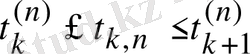 .
.
Егер қарастырылып отырған құбылыс
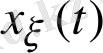 көбейткішінен кездейсоқ сипатқа ие болса, онда
көбейткішінен кездейсоқ сипатқа ие болса, онда
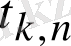 мәндері кездейсоқ түрде таңдалуы мүмкін (әдебиетте белгілі Ито стохастикалық интегралында) . Ретсіз үдерістер жағдайында функция мәндеріне, яғни
мәндері кездейсоқ түрде таңдалуы мүмкін (әдебиетте белгілі Ито стохастикалық интегралында) . Ретсіз үдерістер жағдайында функция мәндеріне, яғни
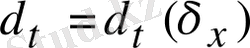 -ке сәйкес
-ке сәйкес
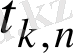 нүктелерін таңдап алу қажет. Сонда Лебег шарасы түріндегі интеграл (2. 25) келесі түрде жазылады:
нүктелерін таңдап алу қажет. Сонда Лебег шарасы түріндегі интеграл (2. 25) келесі түрде жазылады:
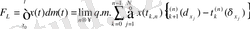 , (2. 26)
, (2. 26)
мұнда
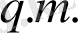 жиынтықтың орташа квадратты мағынасын береді.
жиынтықтың орташа квадратты мағынасын береді.
.
2. 10 Хаостық сигналдардың формасының екіөлшемді коэффициенті
Хаостық сигналдар үшін қисықтардың әр тұрлі формаларын сипаттайтын жалпы сандық сипатын орнатайық. Бұл мақсаттар үшін метрикалық сипаттамалардың (ұзындық, аудандар, көлем) болуы келесі Коши - Буняковскийдың теңсіздігінің орындалуына негізделген деп ескереміз:
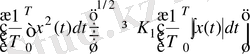 немесе
немесе
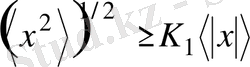 , (2. 27)
, (2. 27)
Мұнда t және T ағымдық және сипаттық мағынаға ие болуы мүмкін . Теңсіздік мына кезінде орындалады
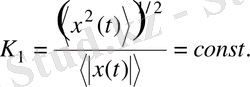 (2. 28)
(2. 28)
K 1 шамасы радиофизикада қолданылады және импульсты сигналдар формасының коэффициенті деп аталады [18] .
(2. 28) теңсіздігі кез келген функция x i (t), x j (t) , үшін келесі түрде жазылған Гельдеринтегралдық тепе-теңсіздіктен шығады.
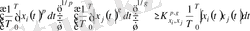 . (2. 29)
. (2. 29)
мұнда
p
,
g
-
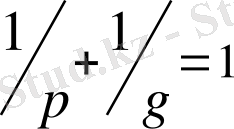 , шартын қанағаттандыратын кейбір сандар
, шартын қанағаттандыратын кейбір сандар
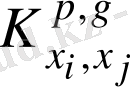 -шамасы тұрақты болған кезде (2. 28) теңдігі орындалатын коэффициент:
-шамасы тұрақты болған кезде (2. 28) теңдігі орындалатын коэффициент:
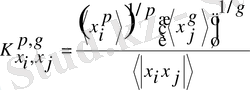 ,
,
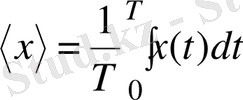 . (2. 30)
. (2. 30)
(2. 29) интегралы аргументті өсіру барысында Риман әдісі арқылы есептеледі
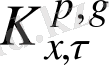 сипаты алғаш рет . Ж. Жаңабаев [15] жұмысында енгізілген және хаостық сигналдың біртексіздігін аффинділігін және әр түрлі формаларын сипаттайтын форманың екі өлшемді коэффициенті немесе жалпыланған метрикалық сипаттама деп аталады. Функцияның
сипаты алғаш рет . Ж. Жаңабаев [15] жұмысында енгізілген және хаостық сигналдың біртексіздігін аффинділігін және әр түрлі формаларын сипаттайтын форманың екі өлшемді коэффициенті немесе жалпыланған метрикалық сипаттама деп аталады. Функцияның
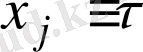 түрінде таңдалу мүмкіндігі әрбір зерттелініп отырған импульс үшін бұл құбылыстың сипаттық уақыты екендігімен негізделген.
түрінде таңдалу мүмкіндігі әрбір зерттелініп отырған импульс үшін бұл құбылыстың сипаттық уақыты екендігімен негізделген.
2. 11 Корреляциялық өлшемділік
Бірдей өлшемді
δ
ұяшықтарға бөлінген фракталды бетті қарастырайық және кез-келген
х
1
және
х
2
еркін таңдалған екі нүкте фракталды объектіге жататын нүктелер болсын делік.
.
Екі нүктеніңде
i
-ші ұяшықта болу ықтималдығы қанша? Бір нүктенің осы беттің
i
-ші элементіне түсу ықтималдығы
р
i
-ге тең. Егер екі нүктенің осы ұяшыққа түсуі байланыссыз оқиғалар деп алсақ, онда оның ықтималдығы
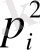 -ге тең болады.
-ге тең болады.
Фракталдық бет (q = 2) жабылатын ұяшықтар көлемін кішірейткендегі, статистикалық қосындының өзгерісін қарастырайық. δ-ны кішірейткенде қосынды азаяды, бұдан ол дәрежелік заңға бағынады деп жорамалдауға болады:
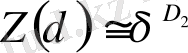 , (2. 31)
, (2. 31)
немесе, эквивалентті, шек
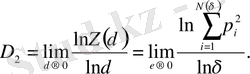 (2. 32)
(2. 32)
D2 корреляциялық өлшемділік деп аталады.
Dq шамасы жалпы қабылданған мағынасында нақты айтатын болсақ фракталдық өлшемділік емес. Сондықтан көп жағдайда мультифракталды жиынды бейнелеу үшін мультифракталды спектрлік функция f(α) (мультифракталдың сингулярлығының спектрі) қолданылады. Біз f(α) шамасы ℒ жиынындағы біртекті фракталдық ішкі жиынының хаусдорф өлшемділігіне тең екендігін көрсетеміз.
Өзұқсас жиын үшін рi шамасының δ ұяшық өлшеміне тәуелділігі дәрежелік байланыста болады
 (2. 33)
(2. 33)
мұндағы αi - қандайда бір дәрежелік көрсеткіш (шынында әр-түрлі i ұяшыққа әр-түрлі) . Регулярлы (бірқалыпты) фракталдар үшін αi дәрежелік көрсеткіштер бірдей және D фракталдық өлшемділікке тең
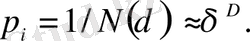 (2. 34)
(2. 34)
Бұл жағдайда (2. 6. 2) статистикалық қосынды келесі түрге өзгереді
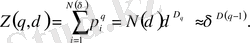 (2. 35)
(2. 35)
Сондықтан
 және барлық жалпыланған фракталдық өлшемділіктер Dq=D бұл жағдайда бір-біріне сәйкес келеді және q-ға байланысты емес. Бірақ мультифрактал сияқты күрделі объектілер үшін рi ұяшықтардың толтырылу ықтималдығы бірдей емес және αi дәреже көрсеткіші әр-түрлі. Көп кездесетін жағдайдың бірі - осы мәндер қандайда бір (αmin, αmax) жабық интервалды толтырады және
және барлық жалпыланған фракталдық өлшемділіктер Dq=D бұл жағдайда бір-біріне сәйкес келеді және q-ға байланысты емес. Бірақ мультифрактал сияқты күрделі объектілер үшін рi ұяшықтардың толтырылу ықтималдығы бірдей емес және αi дәреже көрсеткіші әр-түрлі. Көп кездесетін жағдайдың бірі - осы мәндер қандайда бір (αmin, αmax) жабық интервалды толтырады және
 . (2. 36)
. (2. 36)
Осы α-ның шектік мәндерімен τ(q) функциясының туындысы мәндерінің арасындағы байланысты, атап айтқанда q→±
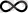 ұмтылғандағы туындының шектік мәндерін қарастырайық. Егер біз q→
ұмтылғандағы туындының шектік мәндерін қарастырайық. Егер біз q→
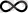 мәнін алсақ, (2. 34) тендеудегі i бойынша қосындыға, максималды рmax толықтыру ықтималдығымен сипатталатын тек ішінде көп нүктелер шоғырланған ұяшықтар көп үлес береді. Қосындыда тек осындай (саны Nmax) ұяшықтарды қалдыра отырып, (2. 6. 4) теңдеудің алымы Nmax
мәнін алсақ, (2. 34) тендеудегі i бойынша қосындыға, максималды рmax толықтыру ықтималдығымен сипатталатын тек ішінде көп нүктелер шоғырланған ұяшықтар көп үлес береді. Қосындыда тек осындай (саны Nmax) ұяшықтарды қалдыра отырып, (2. 6. 4) теңдеудің алымы Nmax
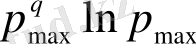 , ал бөлімі Nmax
, ал бөлімі Nmax
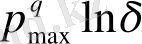 екендігін көреміз. Соңында,
екендігін көреміз. Соңында,
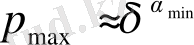 екенін ескерсек, ізделіп отырған туындының шегі αmin -ға тең болады. Сол сияқты, q→-
екенін ескерсек, ізделіп отырған туындының шегі αmin -ға тең болады. Сол сияқты, q→-
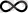 , жағдайда (2. 34) теңдеудегі қосындыны үшін рmin ықтималдықпен сипатталатын тек аз нүтелері бар ұяшықтарды ескеру қажет. Бұл жағдайда
, жағдайда (2. 34) теңдеудегі қосындыны үшін рmin ықтималдықпен сипатталатын тек аз нүтелері бар ұяшықтарды ескеру қажет. Бұл жағдайда
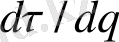 туындысы αmax мәніне ұмтылатыны анық.
туындысы αmax мәніне ұмтылатыны анық.
Сонымен біз маңызды қорытындыға келеміз:
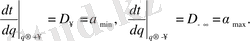 (2. 37)
(2. 37)
яғни мүмкін болатын α интервалы, q→±
 жағдайда жалпыланған фракталдық өлшемділіктің Dq шектік мәндерімен анықталады.
жағдайда жалпыланған фракталдық өлшемділіктің Dq шектік мәндерімен анықталады.
- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz