Зарядталған бөлшектің тұрақты біртекті магнит өрісіндегі қозғалысы: Лармор айналымы, жүргізуші центр, магнит өрісінің біртексіздігі мен градиенттік дрейф

Пән: Математика, Геометрия
Жұмыс түрі: Реферат
Тегін: Антиплагиат
Көлемі: 5 бет
Таңдаулыға:

Теріс зарядталған бөлшек тұрақты біртекті магнит өрісінде оң бұрандамен айналатынын көрсету

Зарядталған бөлшектің тұрақты біртекті магнит өрісіндегі қозғалысы

Ұйытқымаған қозғалыс

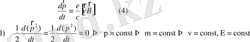
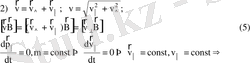
магнит өрісі бағытында бөлшек бірқалыпты қозғалады (магнит өрісі өзіне параллель бөлшектің қозғалысына әсер етпейді)

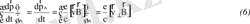
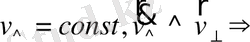тұрақты жылдамдықпен шеңбер бойынша қозғалыс

Бұл қозғалыстың лездік центрін айналыс центрі деп атайық (ол траектория қисықтығының центрінен өзгеше шама болып табылады) . Траекторияның магнит өрісіне перпендикуляр жазықтығына проекциясының қисықтық радиусы (бөлшек орналасқан нүктеден айналу центріне жүргізілген вектор) лармор радиусы (немесе гиро-радиус) деп аталады.

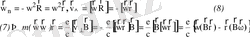
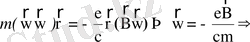оң бөлшектер сол бұрандамен, теріс бөлшектер оң бұрандамен айналады. Теріс бөлшектер-ток бағытымен бағыттас айналады, ал оң бөлшектер-ток бағытына қарама-қарсы.

- бөлшектер

+ бөлшектер

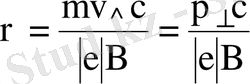- бөлшектің лармор-радиусы (10)

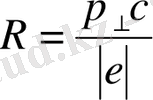- бөлшектің магнит қатандығы (11)

Бөлшектің магнит қатаңдығы - магнит өрісіндегі бөлшектің қозғалысын анықтайды.

42. Зарядталған бөлшек тұрақты біртекті магнит өрісінде қозғалып, магнит өрісінің жеке біртекті еместікпен соқтығу жағдайда 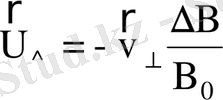болатынын дәлелдеу

Магнит біртекті еместік деп-магнит өрісі фондық өрістен өзгеше өрісі бар кеңістік аймағын айтамыз. (Негізі, магнит өрісі біртекті бола алмайды, себебі оның күш сызықтары міндетті түрде қисайған болады, яғни құйынды. )

Бөлшек біртекті еместікпен соқтығысқанда бағыты өзгереді(шашырайды) . Изотропты-барлық бағытта бірдей қозғалады(диффузия сияқты) . Анизотропты-әр бағытта әртүрлі. Гелиомагнит сферада ҒС изотроптанады.

Зарядталған бөлшек кейбір үлкен емес аймақтан басқа жерде біртекті болып табылатын тұрақты В ₀ магнит өрісінде қозғалсын делік. Бұл сингуляр (ерекше) аймақта магнит өрісі В ₀ -ге параллель, ал оның индукциясы В ₁ -ге тең болсын.

, (1)

Мұндағы:

, ал - бөлшек В ₁ өріске кіретін нүктеден одан шығатын ( В ₀ өріске қайтатын) нүктеге бағытталған вектор.

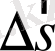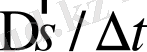
Біртекті еместіктің аймағында В өзгеретін жағдайда бұл аймақты аздығы соншалықты, өріс әр қайсысының ішінде шамамен тұрақты болып қалатын жеке аймақтарға бөлуге болады. бұл жағдайда жолдың элементіне жуық, ал 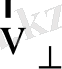жуық болады. Онда (1) -ден

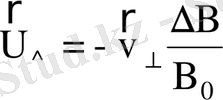шығады.

43. Зарядталған бөлшектің тұрақты біртекті магнит өрісінде магнит емес тұрақты күш әсер еткен жағдайда қозғалғанда болатынын дәлелдеу

Бөлшекке магнит емес күштер де әсер етсе, немесе магнит өрісінде біртекті еместіктер болса, онда жүргізуші центр деген ұғымды қолдануға ыңғайлы болады. Ол - координаттары

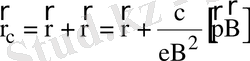(1)

өрнекпен берілетін нүкте, мұндағы - бөлшектің радиус-векторы. Егер бөлшекке тек біртекті магнит өрісі жағынан күш әсер етсе, жүргізуші центр айналыс центрімен беттеседі. Яғни, егер көп емес уақытқа ұйытқушы күштін әсерін алып тастасақ, бұл уақыт ішінде бөлшек шеңбер бойынша жүргізуші центрін айнала қозғалады .

Біртекті тұрақты магнит өрісінде қозғалып жатқан зарядталған бөлшек соқтығуға ұшыраған жағдайды қарастырайық. Соқтығу кезінде уақыттың қысқа аралығында бөлшекке айтарлықтай күші әсер етеді. Егер

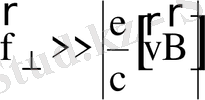
болса, онда бөлшектін импульсі айтарлықтай өзгереді:

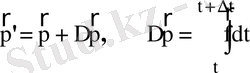(2)

Соқтығуға дейін жүргізуші центр тыныштықта болады, немесе күш сызықтарына параллель бірқалыпты қозғалады. Қысқа мерзімді соқтығу нәтижесінде бөлшектің радиус веторы айтрлықтай өзгермейді, ал жүргізуші центрінің орналасуы импульс векторының өзгерісінен мына мәнге өзгереді:

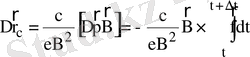. (3)

Бұл нәтиже айналыс центрі үшін де жарамды.

Егер бөлшекке біртекті тұрақты магнит өрісінен басқа магнит емес тұрақты күш әсер етсе, оның жүргізуші центрі кейбір жылдамдықпен ығысады.

(4)

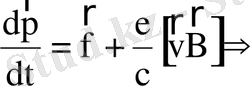
Бұл нәтижені (3) теңдеуден де алуға болады.

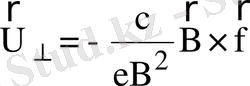(6)

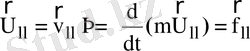(7)

Мұндағы:U ‖ - жүргізуші центр жылдамдығы, V ‖ - бөлшек жылдамдығы.

44. Зарядталған бөлшек градиенті өріске перпендикуляр бағытталған баяу өзгеретін магнит өрісінде қозғалғанда 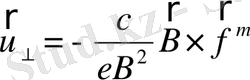, 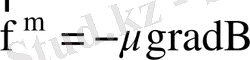болатынын дәлелдеу

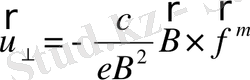
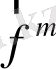- магнит өрісінің өзгерісімен байланысты күш

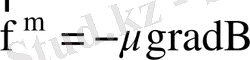, μ- магнит моменті.

Өріс біртексіз, баяу өзгерсе(уақытта, кеңістікте) жалпы алғанда:

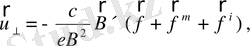бұл жылдамдықтың өріске перпендикуляр құраушысы үшін қорытқы формула.

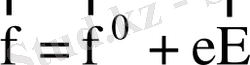- магнит емес күш

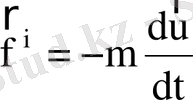- инерциялық күш

Мұндағы m-бөлшек жылдамдығы, U-айналыс центр жылд.

*Магниттік өрісінің градиентінің өріске перпендикуляр құраушысы бар:

Z осі B өрістің бағытына, ал у осі- grad B векторына сәйкес келетіндей координат жүйесін таңдап аламыз. Сонда 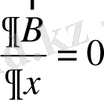→ 1/B ₀ ( 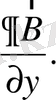) ₀ =1/ L _c (1)

0 индексі, сәйкес келетін мән бастапқы есептеуге тиістілігін көрсетеді. Енді:

ρ/L _c <<1 (2)

Мұнда біз =0 деп есептейміз, яғни күш сызықтары түзу болады. v _ıı ≠0 жағдайында күш сызықтарының қисықтары маңызды роль атқарады, себебі ол орталық күштің пайда болуына әкеледі.