Сигналдарды информациялы-энтропиялық талдау туралы

Пән: Автоматтандыру, Техника
Жұмыс түрі: Материал
Тегін: Антиплагиат
Көлемі: 12 бет
Таңдаулыға:

Сигналдарды информациялы-энтропиялық талдау

Нақтылы объектілер сыртқы ортамен энергиямен, затпен және информациямен алмаса алатын ашық жүйе болып табылады. Объектің тегіне тәуелсіз зерттелетін процес ықтималды құрылымда болса, оның симметриясы бұзылған кезде информация пайда болады. Екінші жағынан, табиғи құрылым - хаостан өз бетінше тәртіп орнау да - нақты бейсызық, ашық жүйелердің мейлінше жалпы даму заңдылығы. Информацияның және информациялық энтропияның физикалық аспектілерін қарастырайық.

Информация ұғымы. Информациялық энтропия

Жалпы қабылданған терминологияға сәйкес информацияның келесі анықтамаларын қолданамыз.

«Информация» ұғымы әртүрлі мағынаға ие. Қоғамдық-саяси информация әлеуметтік жүйенің өзекті жаңалықтары туралы мәліметтердің жиыны болып табылады. Кибернетикада информация ұғымы сигналдарды сақтау, өңдеу және жіберумен байланысты. Ықтималдықтар теориясында информация аддитивті мөлшерлік өлшем ретінде кездейсоқ оқиғаларды бір-біріне қатысты ықтималдылығымен салыстыру арқылы енгізіледі. Барлық информация теориясы негізінде информацияны мөлшерлі бағалау жатыр. Қарапайым комбинаторикалық формада бұл тұжырымды Р. Хартли ұсынды, ал толық аяқталған түрін К. Шеннон тұжырымдады.

Шеннон информация теориясы О және L екі таңбаның арасындағы (биттер арасындағы) қарапайым альтернативті таңдаудан шығады, ондағы L 1-ге, “иә”, “шындық” т. с. с. теңестірілсе, ал О 0-ге, “жоқ”, “жалған” теңестіріледі. Мұндай таңдау екі белгіден тұратын хабарды қабылдауға сәйкес келеді.

Мұндай хабарда болатын информация мөлшері бірлік ретінде қабылданады және ол бит деп аталады. Сондықтан бит - екілік белгі және информация мөлшерінің өлшем бірлігі, ол екі байланысқан тең ықтималдықты таңдамадағы информация мөлшері ретінде анықталады.

Айталық

(11)

- Х және Y әріптерімен сәйкес белгіленген жүйенің күйін сипаттайтын айнымалылар жыйыны болсын. Егер 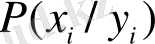- Х жүйесі 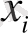күйде болғанда Y у _i күйіне өту ықтималдығы (шартты ықтималдық) болса, онда Y жүйесінің алған информациясы мынаған тең:

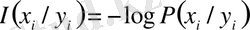. (12)

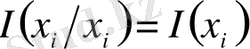- X жүйесіндегі 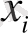оқиғасына қатысты 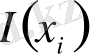информация мөлшері деп аталады.

Ықтималдық 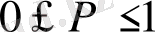арасында жатқандықтан I әрқашан оң шама.

Логарифм негізін таңдауға байланысты информация мөлшері екілік, ондық және натурал логарифм бойынша: сәйкесінше бит , дит , нат - пен өлшенеді.

Статистикалық физикада энтропия ∆Г - жүйенің ішкі макроскопиялық күйінің статистикалық салмағының логарифмі ретінде енгізіледі:

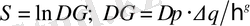, (13)

мұндағы ∆p⋅∆q- фазалық көлем, ћ -Планк тұрақтысы, g -жүйенің еркіндік дәрежесінің саны. Классикалық физикада ћ қолданбайтындықтан энтропияны нақты анықтауға болмайды. (5) -ші формуланың түрі күрделі жүйенің энтропиясының аддитивтік талаптарынан шығады:

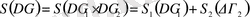. (14)

Идеал газдың энтропиясын (4) -ші формула бойынша есептей отырып (5) -ші формулаға келуге болады, мұндағы ∆Γ - идеал газдың қысымы, көлемі, температурасы бойынша анықталады.

Энтропия түсінігі сонымен қатар кездейсоқ шамалардың ықтималдықтарының таралуына да байланысты. Е _i энергияның теңықтималдықты таралуы кезінде жүйенің ішкі таралу ықтималдылығы былай анықталады.

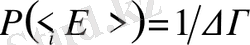Энтропияны мына түрде табамыз

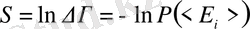. (15)

Орташа ықтималдықтың мағынасы бойынша (15) былай жазылады:

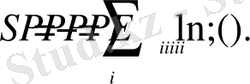(16)

(8) - бойынша анықталған энтропия информациялық энтропия деп аталады [8, 9] . (2) және (8) өрнектерін салыстыру арқылы информациялық энтропия информацияның орташа ықтималдық мәнін анықтайтындығы көрінеді. Жүйенің теңықтималды таралуы кезінде жүйе туралы анықталмағандық максимумге жетеді, яғни жүйе туралы барлық информация жоғалып энтропияға айналады (7) . Тепе-тең жүйе информацияны сақтай алмайды. Информацияны білу анықталмағандықты азайтады. Сондықтан информация мөлшерін жоғалған анықталмағандық, яғни энтропия мөлшерімен өлшеуге болады:

I = S _pr - S _ps ,

мұнда pr - индекс «априорлы» дегенді білдіреді (тәжірибеге дейін) ps «апостериорлы» (тәжірибеден кейін) . Осы себептен әдебиеттерде (16) -ші өрнекпен анықталатын шама кейде информация деп аталады( егер ол қабылданса), кейде энтропия деп аталады (егер ол жоғалса) . Осылайша Х шамасы туралы информация Ү берілген кезде мына теңдікпен анықталады.

I ( X ) = S ( X ) - S ( X/Y ) .

(16) -ші өрнектен энтропияның қасиеттері шығады:

алдын-ала белгілі хабардың энтропиясы 0 -ге тең.
барлық басқа жағдайлардаS >0 болады.

Ашық жүйелердің өзқауымдық деңгейлерінің критерилері

Жалпы қабылданған терминологияға сәйкес I _i информациясы, P _i ықтималдыққа ие құрылым пайда болғанда (жоғалғанда) (2) формуламен есептелінеді және келесі түрде табылады:

60 , (17)

ал оның орта мәні - информациялық энтропия (8) -өрнекпен анықталады.

Әртүрлі иерархиялық деңгейлердегі өзұқсастық, өзқауымдық жүйелердің әмбебаптық қасиеттерінің бірі болып табылады. Олардың сипаттамасының масштабты инварианттылығы информацияның үздіксіз мәндерін қабылдауға мүмкіндік береді. Ал информацияны анықтаушы физикалық шама ретінде қабылдауға болады. Мұндай жағдайлар, алдымен күй функцияларының арасында (мысалы энергия мен энтропияның арасында) бірмәнді емес байланыс орнайтын күшті бейсызық динамикалы-информациялық жүйелерге (турбулентті орта, биологиялық объектілер т. б. ) қатысты.

Сондықтан, информацияның байқалу ықтималдылығы жөнінде айтуға болады:

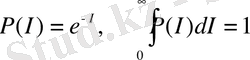. (18)

P ( I ) ықтималдықты f ( I ) ықтималдықтың таралу тығыздығының функциясы арқылы жазсақ:

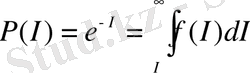, (19)

мұндағы интеграл шектері 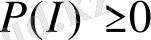аймаққа сәйкес келеді. Демек, 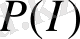- информацияның байқалу ықтималдық функциясы 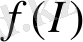- ықтималдықтың таралу тығыздығының функциясымен сәйкес келеді. Информация күрделі жүйелердің барлық иерархиялық деңгейлерінің жалпы және толық сипаттамасы болып табылады: жүйенің бір бөлігі жалпы жүйе туралы мәліметті қамтиды.

(18) формуланы ескере отырып, өзұқсас жүйелердің информациялық энтропиясын келесі түрде жазамыз:

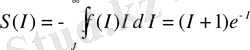. (20)

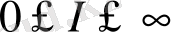үшін 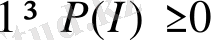және 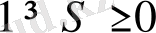болады.

Өзқауымдық жүйенің өзұқсастығы қандай да бір сипаттамалы 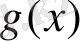функциясының мына функционалды теңдеуге сәйкестігімен сипатталады:

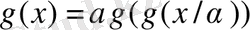, (21)

мұндағы α - масштабты көбейткіш. Кез-келген үздіксіз функция өзінің қозғалмайтын нүктесінде (21) теңдеуді қанағаттандырады. Сипаттамалық функция ретінде f ( I ) - ықтималдық тығыздығын және 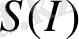- информациялық энтропияны қабылдап, олардың қозғалмайтын нүктелерін табайық:

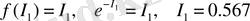, (22)

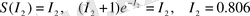. (23)

Бұл қозғалмайтын нүктелер бірмәнді орнықты, себебі олар, сонымен қатар, информацияның 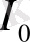кез-келген бастапқы мәніне сай шексіз бейнелеудің шегі болып табылады:

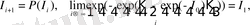(24)

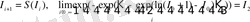. (25)

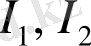сандарының мағынасын әртүрлі түсіндіруге болады. Олардың ішіндегі ең әмбебабы - Фибоначчи санын (жүйенің динамикалық өлшемі - «алтын қима») қолдану аймағының кеңейуі. 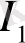саны информациялық (локальді) сипаттауына, ал саны күрделі жүйені энтропиялық (орталанған) сипаттауға сәйкес келеді. болса (22) -ден (21) шығады, 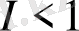бойынша экспонентаны жіктеудің бірінші мүшесін ескерсек, онда (23) -ден 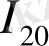- Фибоначчи саны үшін теңдеу аламыз:

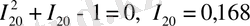, (26)

(21) теңдеуден I - I ₁₀ = I ₁₀ , I ₁₀ = 0, 5.

Сонымен, тәжірибеде күрделі жүйенің өзқауым күйі S ∈[ I ₂₀ I ₂ ] жағдайда, қарапайым жүйенің өзұқсас жағдай I ∈[ I ₁₀ , I ₁ ] болғанда байқалуы тиіс.

Төменде (21), (22) тәуелділіктерді тұрғызуға арналған бағдарлама және сплайн интерполяцияның көмегімен тұрғызылған график келтірілген (3-сурет) .

I ₁ , I ₂ сандарының мағынасын жалпылама пайымдаулармен толығырақ ашуға болады. Шеннон бойынша Y берілген кездегі Х шамасы туралы информация шартсыз және шартты энтропиялардың айырымы ретінде анықталады:

S ( X ) - S ( X / Y ) = I ( X ) > 0. (26)

S ( X ) шамасын «Физикалық хаостың» энтропиясының анықталмағандығының нормасы ретінде қабылдап, (26) -ны мына түрде жазамыз:

I + S = 1, (27)

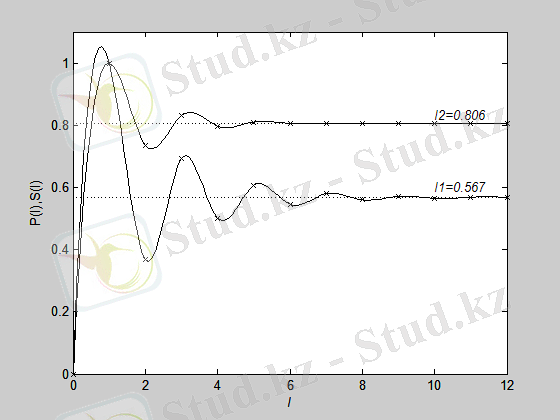
6-сурет. Информация және энтропияның сипаттық уақыт бойынша өзгерісі

мұндағы I - анықталғандықтың салыстырмалы өлшемі (информация), S - қандайда бір Х сипаттасы бойынша жүйе туралы анықталмағандықтың салыстырмалы өлшемі (энтропиясы) . Жалпы мағынада (27) өрнек кез-келген табиғаттың күрделі жүйелерін өзара байланысқан альтернативті сипаттамаларын байланыстырады: тәртіп және хаос, симметрия және асимметрия, рационалды және иррационалды, детерминизм және индетерминизм және т. б. Альтернативті сипаттамалардың үйлесімі олардың салыстырмалы өлшемінің өзгеруінің пропорционалдылығын болжайды:

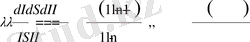(28)

мұнда I , S өлшем бірліктерін таңдау еркіндігі мүмкін болғандықтан интегралдау тұрақтысы нөлге тең деп алынған. Дербес жағдайда λ параметріне және I айнымалысына айқын мағына беретін

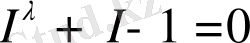(29)

алгебралық теңдеуі (28) формулаға эквивалентті. М. Фейгенбаум орнатқан табиғи құбылыстардың әмбебап даму заңдылығының периодты екі еселенуінің бифуркациясын негізге алайық. Жүйенің даму деңгейінің иерархиялық күрделілігін ретіне n- ге сәйкестендіріп, λ = 2 ⁿ деп қарастырайық. n = 0, λ = 1 жүйенің статикалық күйіне сәйкес келеді және (29) -дан I = S екені шығады. Динамикалық жүйенің бірінші иерархиялық даму деңгейі ( n = 1, λ = 2) Фибоначчи ( I ₃ = 0. 618) санына тең сипаттамалардың пропорциясымен анықталады. Статикалық және динамикалық күйлердің (құрылымның және стохастиканың бастауы) арасында I ₁ саны арқылы сипатталатын жүйенің информациялық күйі жүзеге асады. λ =1. 5 деп алып, (29) -дан I = 0. 57 ≈ I ₁ болатындығын көреміз. Ли-Йорктің «үш период хаосты білдіреді» атты теоремасы бойынша n = 3 жағдай ішкі тәртібі бар ең күрделі статистикалық күйді I ₂ энтропия функциясының қозғалмайтын нүктесімен сипаттайды. λ = 2 ³ = 8 үшін (29) -теңдеудің шешімі I = 0. 811 ≈ I ₂ болып табылады.

Импульстердің информациялы-энтропиялық сипаттамалары

Шекті уақыт аралығында бақыланатын сигналдың (импульстің) ұзақтығы бірдей болсада, оның формасы әртүрлі күрделі қисықтар болуы мүмкін: мейлінше хаосты, өзұқсас құрылымы бар фракталды, алмасу құрылымды және т. б. Күрделі сипаттамаларды өлшеу әрқашан белгілі анықталмағандықпен орындалады. Объектіні статистикалық сипаттау кезінде анықталмағандықтың толығырақ және әмбебап өлшемі жоғарыда көрсетілген информациялық энтропия болып табылады.

Импульстің форма коэффициенттері . Ииформациялық энтропия метрикалық және топологиялық сипаттама болып табылады. Оның заңдылықтарын мөлшерлі түрде сипаттау үшін басқа, мысалы, таза метрикалық сипаттаманы қолдану қажет. Бұл мақсат үшін жекелеген импульстердің формаларының айырмашылығын бірмәнді суреттейтін жалпы метрикалық сипаттама тағайындайық. Метрикалық сипаттамалардың (ұзындық, аудан, көлемнің) болуы Коши-Буняков теңсіздігінің орындалуынан шығады:

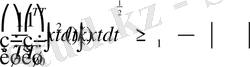или 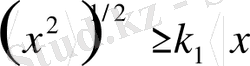, (30)

мұндағы 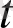және өтпелі және сипаттамалы уақыт деген мағынаны білдіреді.

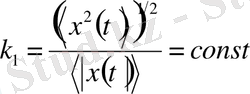(31)

болғанда ғана теңдік орындалады. k ₁ шамасы радиофизикада қолданылады және ол импульстік сигнал формаларының коэффициенті деп аталады [10-12] .

(30) теңсіздік Гельдердің кез-келген 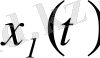, 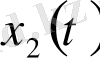функциялары үшін келесі түрде жазылған интегралдық теңсіздігінен шығады:

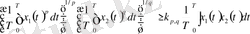, , (32)

мұндағы 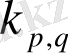- коэффициент, оның тұрақты мәнінде (32) теңдік орындалады. 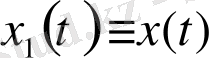, 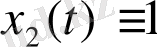болғанда, біз (31) -ші формуланы аламыз. 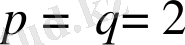жағдайы үшін (32) теңдік келесі жағдайда орындалады:

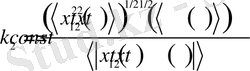. (33)

1. 3 Сигналдарды фракталдық және мультифракталдық әдіспен талдау Фракталдық өлшемділік

Өлшемділігі d ( d = 1 - түзу, d = 2 - жазықтық, d = 3 - үшөлшемді кеңістік) болатын Евклид кеңістігінде өлшемі L шектелген ℒ аймағын алып жатқан фракталды объектіні қарастырайық. Фракталды объект өзінің құрылуының қандайда бір кезеңінде осы аймақта таралған N >>1 нүктелерден тұратын жиын болсын. Нүктелер саны N мейлінше N → 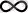шекке жақын болсын. Барлық ℒ аймағын қабырғасы δ және көлемі δ ^d куб ұяшықтарға бөлелік. δ азайған сайын, N ( δ ) ұяшықтар саны дәрежелік заңдылықпен өседі

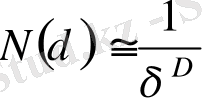, (34)

мұндағы D - Хаусдорф бойынша, немесе, фракталдық өлшемділік деп аталады. (1) қатынасты логарифмдеп және δ -ны нөлге ұмтылдыру арқылы келесі қатынасты аламыз

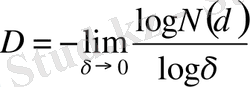. (35)

Логарифмді кез-келген оң, бірден өзгеше негіз бойынша алуға болады, мысалы, 10 немесе 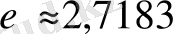бойынша. (2) формула D фракталдық өлшемділіктің жалпы анықтамасы болып табылады. Бұл формулаға сай D шамасы берілген объектінің локальды сипаттамасы болып табылады. Егер бұл анықтаманы Кантор жиыны (1-сурет) немесе

1/3

1/9

1/27…

7-сурет. Кантор жиыны

8 - сурет.

Серпиньскийдің

квадратты кілемі

Серпиньский кілемі (2-сурет) секілді фракталды объектілерге қолдансақ, онда D бөлшек шама болады.

Серпиньский кілемінің (2 сурет) фракталдық өлшемін табайық. Егер ұяшықтың өлшемі δ = 1/3 болса, онда беттегі ұяшықтар саны N = 8 болады, ұяшықтар ауданы үш есе азайғанда δ = 1/9 және N = 64 ұяшықтар санын аламыз, ал k- ші деңгейде - δ = (1/3) ^k және N ( δ ) = 8 ^k болады. (2) формуланы қолданып, келесі мәнді аламыз

Өзаффинді сигналдарды сипаттау

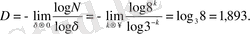
Алынған нәтижелерді қолдану мүмкіндігін көрсету үшін Вейерштрасс-Мандельброттың өзаффинді фракталдық қисықтарын b , A параметрлерінің әртүрлі мәндері үшін қарастырайық:

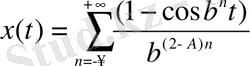. (36)

Ұзындығы L ( δ ) қисықпен шектелген F ( δ ) фракталдық ауданды бөліп алу схемасы 3-суретте көрсетілген. Жаңа тікбұрышты координат жүйесі, x ( t ) мен 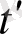өсінің қыйылысуы әр-түрлі күрделі құрылымдары бөліп алатындай етіп таңдалған. Екі қатар тұрған нөлдер интервалда 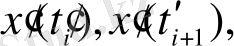яғни 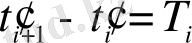, өсіне симметриялы қыйсық тұрғызайық. Бұл процедура, мәндер өсі бойынша түзу сызық болмайтын, 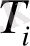параметрімен сипатталатын тұйықталған фракталдық қисықты алуға мүмкіндік береді. Осындай әр-түрлі мәндері бар фракталдық элементтерді бөле отырып фракталдық өлшемділіктің асимптотикалық мәндерін іздестіруге болады. Басқа жағдайларда T -ға тәуелді фракталдық өлшемділік туралы ғана айтуға болады. 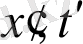айнымалыларды 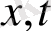ретінде қайта белгілеу арқылы (16), (17) формуланы қолданамыз. 4-суретте (15-17), (22) формулалармен табылған D ₁ және D ₂ мәндері көрсетілген. Вейерштрасс-Мандельброт өзіндік аффинді қисығы әртүрлі фракталдық өлшемділіктерге ие. Өзұқсастық ( D ₁ және D ₂ мәндерінің тепе-теңдігі) А параметрінің үлкен мәнінде 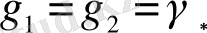, γ _* = S _* ( I ) = 0. 806 ғана бола алады. Екінші өзіндік ұқсастылық критерийі γ _* = f _* ( I ) = 0. 567 мұнда байқалмайды, себебі бұл қисықтар үшін 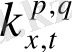мәні жоғары.

10-сурет. Фракталдық өлшемділіктің (22) формуладағы А параметіріне тәуелділігі. ( b = 1, 5) . - D ₁ , - D ₂

D ₁ , ₂

1. 806

T _i

9-сурет. Өзаффинді Вейерштрасс-Мандельброт қыйсығы.

b = 1. 5, A = 1. 8

1, 2

1, 4

1, 6

1, 8

2, 2

Біз өзаффинді жиындарды фракталдық өлшемділік арқылы сандық сипаттау мүмкіндігін көрсеттік. Көп өлшемді фракталдық шама арқылы анықталатын фракталдық өлшемділік теңдеулері, күрделі геометриялық объектілердің форма коэффициенті, өзаффинді фракталдардың реттік параметрлерін енгізу мүмкіндіктері осы бөлімдегі негізгі нәтижелер болып табылады. Өлшеу масштабы азайған жағдайда локальды реттілік параметрі өседі, ал өлшеу масштабы өскен жағдайда глобальды параметрдің реттілігі өседі. Үздіксіз фракталды қисықтың симметриясының өзгеруі екінші реткі фазалық көшу секілді. Бұл кризистік құбылыстарды фракталдық өлшемділіктер арқылы физикалық (концентрация, температура, қысым т. с. с) параметрлер арасындағы байланысты сипаттауға мүкіндік береді.

Корреляциялық өлшемділік

Бірдей өлшемді δ ұяшықтарға бөлінген фракталды бетті қарастырайық және кез-келген х ₁ және х ₂ еркін таңдалған екі нүкте фракталды объектіге жататын нүктелер болсын делік. _. Екі нүктеніңде i -ші ұяшықта болу ықтималдығы қанша? Бір нүктенің осы беттің i -ші элементіне түсу ықтималдығы р _i -ге тең. Егер екі нүктенің осы ұяшыққа түсуі байланыссыз оқиғалар деп алсақ, онда оның ықтималдығы 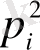-ге тең болады.

Фракталдық бет ( q = 2) жабылатын ұяшықтар көлемін кішірейткендегі, статистикалық қосындының (26) өзгерісін қарастырайық. δ -ны кішірейткенде қосынды азаяды, бұдан ол дәрежелік заңға бағынады деп жорамалдауға болады:

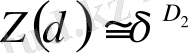, (37)

немесе, эквивалентті, шек

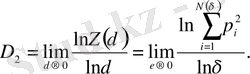(38)

D ₂ корреляциялық өлшемділік деп аталады.

Корреляциялық өлшемділіктің бейсызық динамикадағы ерекшелігі оны есептейтін салыстырмалы жеңіл және эффективті (басқа өлшемділіктерге қарағанда жеңіл және эффективті) тәсілі бар, ол - Грассбергер-Прокаччи алгоритмі .

... жалғасы

Сіз бұл жұмысты біздің қосымшамыз арқылы толығымен тегін көре аласыз.