Үлкен гелиоцентрлік қашықтықтардағы күн желі

Пән: Физика
Жұмыс түрі: Реферат
Тегін: Антиплагиат
Көлемі: 6 бет
Таңдаулыға:

0.7 Үлкен гелиоцентрлік қашықтықтардағы күн желі

ζ --infinity, u(ζ) болғанда, шексіз өсуі мүмкін немесе қандай да бір тұрақты шамаға немесе нөлге ұмтылуы мүмкін. Ашық көрініп тұр, u -- infinity (8) теңдеуді қанағаттандырмайды. Шынымен де, сол жақтағы бірінші мүше шексіз өседі, екінші және үшінші мүшелер нөлге ұмтылады, ал сол кезде (8) оң жағы ui2 = const.
u(ζ-- infinity) = const нұсқасы мүмкін болады екен. Мынадай жағдайда u(ζ-- infinity) -- u1. (9а)
u(ζ-- infinity) -- 0 шешімі де (8) теңдеуді қанағаттандырады. Осы (1.14)
теңдеудің сол жағында бірінші және үшінші мүшелері нөлге ұмтылады және

uuζ-- infinity--u0ζ2 (αα-1 1u2)1α - 1 (1.15)

Сонымен, үлкен қашықтықтарды шешуге арналған (8) теңдеудің шешімінің екі жолы бар: жоғарғы (u --u1) және төменгі (u -- 0). Физикаға сай шешімді таңдау үшін осы шешімдерге сай плазманың тығыздығын есептейміз.
(1.4) теңдіктен

ρr=ρ0 1ζ2 u0u (1.16)

(9а), (9б) - ғы u шамасын (10) қойып,

uζ-- infinity-- 0ρ0 α -1α12α1α - 1
(1.17)

(1.15) теңдеуден көрініп тұрғандай, u(ζ) төменгі жағындағы шешімге сәйкес болса, u -- infinity болғанда плазманың тығыздығы ақырғы және салыстырмалы үлкен шамаға ұмтылады, ал бұл жағдай тәжірибелік мәліметтерге қарсы. Және де жоғарғы жағының шешімі ρ(ζ-- infinity) -- 0 сәйкес, ол модельдің шарттарын қанағаттандрады. Сонымен, Күннен үлкен қашықтықта Паркер теңдеуінің жоғарғы жағының шешімі ғана физикалық түрде мағынаға ие.
Кіші арақашықтықта (ζ-- 0) (8) теңдіктің сол бөлігінде ζ-- 0 болғанда үшінші мүше шексіз өседі. Өйткені, теңдеудің оң бөлігінде тұрақты шама, оның шексіз өсуі (Н ζ) ζ-- 0 (8)оң бөлігіндегі мүшелердің екеуінің бірі компенсирленген болу керек, яғни қайтадан шешімнің екі жолы бар:

жоғарғы жағы
uζ-- 0-- (Hζ)12-- infinityu0 αα-1 1H1α - 1ζ1α - 1 -2 төменгі жағы

Бірінші шешім, ζ-- 0 болғанда, күн желінің жылдамдығының шексіз өсуіне сәйкестендірілген, физикалық түрде келіспейді. Екінші шешім, 1(α-1) - 2 0 теңсіздікпен анықталатын политроп көрсеткішінің мәні u(ζ) --0 болғанда,яғни α 32, ойға сиярлықтай нәтиже береді.
Сонымен, тәждің стационарлы шешімі, егер политроп көрсеткіші а адиабаттықтан кіші болса ( = 53), яғни егер тәжде және күн желінде үздіксіз энергияның түсуі орын алса ғана мүмкін болады. Парекрдің алғашқы үлгісінде қажетті мөлшерде энергияның түсуі күн плазмасының жоғары жылуөткізгіштігімен қамтамасыз етіледі деп ойлаған. Бірақ, күн желі үдетілу үшін жылулық энергияның бір ағыны ғана жеткіліксіз екенін және қосымша энергия көзі қажет екені төменде көрсетілетін болады.
Сонымен біз көріп тұрмыз,шекті шарттарға үлкеніне Паркердің теңдеуінің жоғарғы жағы, ал кішіде төменгі жағы қанағаттандыратынын көріп отырмыз. Ос екі тізбекті өсуі орны жазықтықта (ζ, u) төмендегідей орындалатын, қандай да бір критикалық нүктеде шешімі барына тәуелді
(1.8) теңдеуді ζ бойынша дифференциялдаймыз:

(2u - αu0α - 1uαζ2(α - 1))dudζ = 2αu0α-1uα-1ζ2α- 1+1- Hζ2. (1.18)

(ζc , uc)критикалық нүктесін анықтаймыз, (1.13) теңдеудің оң жағы және теңдеудің сол жағындағы dudζ коэффициенті кезінде нөлге тең. Сонда

uc2 =H4, ζc= H4α+1c-2α(2αu0α-1)2c -2α (1.19)

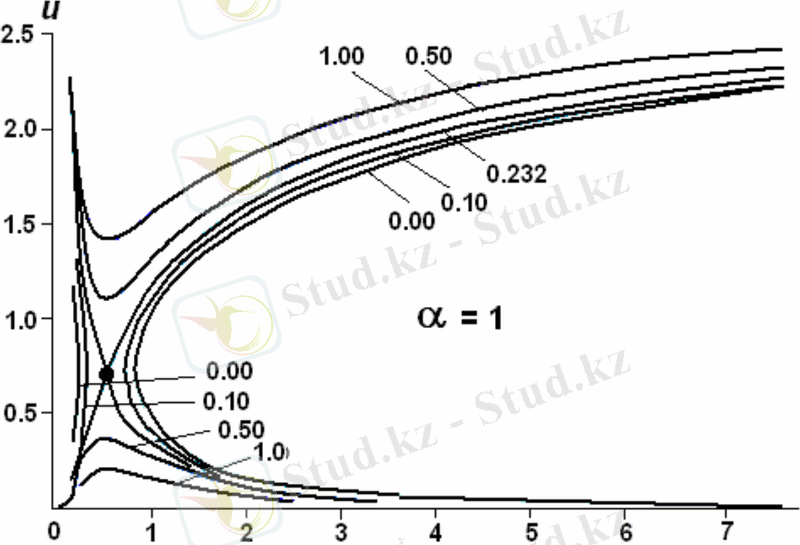
(1.8) теңдеудің шешу топологиясы критикалық нүкте маңында 1.4 суретте көрсетілген. Шешімі гипербола жиынтығына жатады. Бірақ соның өзінде де шекті шарттарды қанағаттандыратын Күннен кіші де және алыс та қашықтықта бір ақ шешімі бар. Осы шешімге критикалық нүкте (критикалық шешімі) арқылы өтетін қисық сәйкес келеді.

1.5 сурет - Критикалық нүкте маңында Паркер теңдеуінің шешімі қисықтар жиынтығы

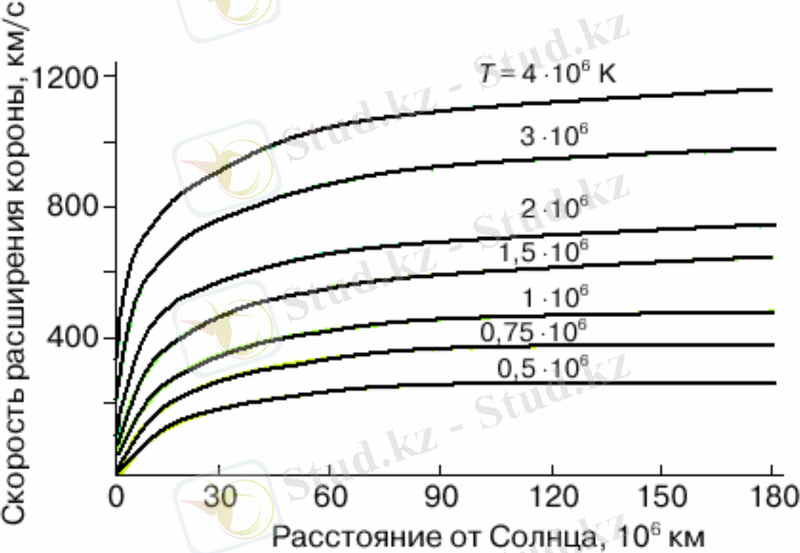
Күн желінің жылдамдығының радиалды кесіндісі изотермиялық тәж ( = 1) әр түрлі соңғы температура жағдайында 4 суретте көрсетілген. Келтірілген қисықтардан көрініп тұрғандай шекті шарттарда айтарлықтай сезімтал. Мысалға, Т0 = 0,5 106 К болғанда Жер орбитасында күн желінің жылдамдығы 260 кмстең болып шығады, ал T = 4 106 К болғанда - шамамен 1150 кмс, ал ол өз кезегінде тәжірибелік мәліметтерге қайшы келмейді (1 кестені қараңыз). Сол уақытта Жер орбитасында есептелген плазманың тығыздығы шын 5-10 см- 3 орнына 25-40 см- 3 келеді.

1.6 сурет - Тәжді әр түрлі температурасы Т кезінде Паркер моделінде күн желінің жылдамдығының радиалды кесіндісі

Кестеден көрініп тұрғандай күн желінің ылдамдығы айтарлықтай кең диапазонда өзгереді - ~ 300 бастап ~ 700 кмс дейін. Осы вариацияларды Паркер моделінде тәж температурасының сәйкес варияциясымен оңай иүсінетіндей көрініп еді (4 сурет). Бірақ тікелей бақылаулар рекурентті жоғары жылдамдықты ағындардың көзі тәж тесіктері болып табылатыны көрсетті, оларда тәждің температурасы орташадан кәдімгідей төмен. Осыған байланысты, күн желінің жылдамдығы тәждің температурасынан басқа политроп көреткішінің α шамасына да тәуелді: α өскен сайын Жер орбитасында күн желінің жылдамдығы аз. Модельдің есептеуі мен тәжірибелік мәліметтер арасындағы жақсырақ сәйкестікті Паркер α = 1,1 болғанда Күнге жақын және α = 53 одан өте үлкен арақашықтықта алды.
Бірақ көрсеткіштің шамасы ... жалғасы

Сіз бұл жұмысты біздің қосымшамыз арқылы толығымен тегін көре аласыз.