Фоккер-Планк теңдеуі. Ланжевен теңдеуі

Пән: Физика
Жұмыс түрі: Реферат
Тегін: Антиплагиат
Көлемі: 5 бет
Таңдаулыға:

Фоккер-Планк теңдеуі. Ланжевен теңдеуі

Бұл теңдеу үлестірілу функциясының уақыттағы өзгерісін диффузиялық жуықтауда өрнектейді. Оны бірнеше әдіспен, оның ішінде іргелі физикалық принциптері негізінде, алуға болады. Ал феноменология тұрғысынан оны диффузия теңдеуіне ұқсатып алуғы болады. Диффузия теңдеуінің негізінде үздіксіздік теңдеуіне қанағаттандыратын кейбір шаманың, мысалы масса тығыздығының (ρ), 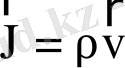ағыны сол шаманың градиентіне пропорционал болып табылады деген болжау жатыр: 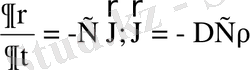, мұндағы D пропорционалдық коэффициенті диффузия коэффициенті деп аталады, ол әсерлесетін бөлшектердің қасиеттеріне тәуелді болады. үшін өрнекті үздіксіздік теңдеуіне қойып, диффузия теңдеуін аламыз. Тығыздықтың орнына жылдамдықтың үлестірілу функциясын қолданып: 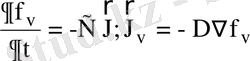, диффузия коэффициенті туралы физикалық болжауларды жасап, Фоккер-Планк теңдеуін алуға болады:

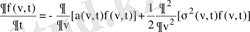, (12)

мұндағы a(v, t) - үйкеліс күші, σ - жылдамдықтар дисперсиясы. Үйкеліс күші мынаған байланысты пайда болады. Көршілес жұлдыздардан тез қозғалатын жұлдыз олардың орбиталарын былай етіп ауытқытады: тез қозғалатын жұлдыздың артында жұлдыздар санының орташа тығыздығы өседі, ал оның алдындағы орташа тығыздық азаяды. Бұның нәтижесінде мұндай жұлдыз артында оны тежететін артық гравитациялық күш пайда болады. Әр жұлдызға флуктуациялайтын 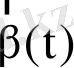орташа күш (ол орташаланған алыс жұлдыздар жағынан әсер ететін күш пен ең жақын көршілер жағынан әсер ететін флуктуациялайтын күштің қосындысына тең) әсер етеді деп болжап, және жоғарыда енгізілген жұлдыз жылдамдығына пропорционал тежегіш күшті еске алып, жұлдыз үшін Ньютонның екінші заңын былай жазуға болады:

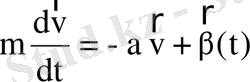. (13)

Бұл теңдеу Ланжевен теңдеуі деп аталады. Фоккер-Планк теңдеуі осы теңдеуден де шығады. Бірлік массаға әсер ететін (13) -гі тежегіш күш (12) теңдеудегі үйкеліс күші болып табылады. Теңдеуден көрінетіндей, жылдамдық екі себептен өзгереді: үздіксіз әрекеттен (бірінші мүше) және стохастикалық күштің әсерінен (екінші мүше) .

Үйкеліс күші нолге тең, ал σ жылдамдыққа тәуелсіз болған жағдайда, (12) теңдеу әдеттегі (тек координаттар кеңістігіндегі емес, жылдмадықтар кеңістігіндегі) диффузия теңдеуіне айналады: .

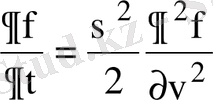Фоккер-Планк теңдеуі Марков жүйелері (яғни жады жоқ жүйелер) үшін жарамды болып табылады. Мұндай жүйелерде соқтығулар арасындағы уақыт соқтығу уақытынан (оның ішінде соқтығысып жатқан бөлшектердің бір біріне әсері елеулі болып табылатын уақыт аралығынан) айтарлықтай көп болады, яғни әр соқтығу одан кейнгі соқтығу басталудың алдында бітіп үлгіреді де, соқтығуларды бөлшектің орбитасын өзгертетін кездейсоқ импульстер ретінде қарастыруға болады. Сондықтан мұндай жүйенің эволюциясын кез-келген уақыт мезетінен бастап зерттеуге болады (бастапқы мезеті ретінде кез-келген мезетті алуға болады), жүйенің бұл мезеттен кейінгі дамуы оның алдындағы эволюциясына тәуелсіз болады, яғни кейінгі эволюцияны өрнектеу үшін оның алдында не болғанын білу керек емес, өйткені жүйенің жадысы жоқ. Дәл соған байланысты Фоккер-Планк теңдеуі Больцман теңдеуі сияқты??? дифференциалды-интегралды емес, таза дифференциалды теңдеу болып табылады, оның шешімі уақыт бойынша локальды сипатта болады.

Тағы бір айта кететін жай, көрініп тұрғандай, (12) теңдеудегі үлестірілу функция тек жылдамдықтың модуліне тәуелді, ал оның бағытына байланыссыз болып табылады, яғни бұл теңдеу тек абсолютті изотропты жүйелер үшін жарамды болады. Бұл шарт соқтығулар арасындағы уақыт ірімасштабты??? қозғалыстардың сипатты уақытымен салыстырғанда өте аз болғанда орындалады, өйткені бұл жағдайда бөлшектер кездейсоқ түрде барлық бағыттарда шашырап, изотроптық түрде (бағытқа тәуелсіз, барлық бағыттарда бірдей) қозғалатын болады (жалпы, әдеттегі диффузия бөлшектер бір-бірімен соқтығысып, бейберекет жылулық қозғалғанның нәтижесінде болатынын естерімізге алсақ, диффузиялық жуықтау жарамдылығының бұл шарты түсінікті болады) .

(12) түріндегі Фоккер-Планк теңдеу жарамдылығының тағы бір шектеуі - үлестірілу функция біртекті (яғни координаттарға тәуелсіз) болу тиіс. Бірақ Фоккер-Планк теңдеуін анизотропты үлестірілу функциясы үшін және алтыөлшемді фазалық кеңістіктегі (координаттарға да тәуелді) үлестірілу функциясы үшін жалпылауға болады.

Лиувилль теңдеуі

Больцман теңдеуінен басқа гравитациялық жүйелерді сипаттайтын Ланжевен, Фоккер-Планк сияқты теңдеулер бар. Бірақ оларың әр қайсысы тек кейбір болжауларды жасау көмегімен алынады және тек берілген бір шарттарда жарамды болады. Одан барлық бұл теңдеулер жеке жағдайы ретінде шығатын гравитациялық жүйелер сипаттауының жалпы әдісі де бар екен.

Лиувилль теңдеуін 6N-өлшемді «үлкен фазалық кеңістік» ұғымын енгізіп, алуға болады. Бұл кеңістіктің әр нүктесіне бір бөлшек (объект) емес, барлық N объекттен тұратын жүйе сәйкес келеді. Мұндай фазалық нүктенің траекториясы барлық жүйе күйінің уақыттағы өзгерісін көрсетеді. Табиғатта бірдей сипаттамалар жиынтығымен анықталатын жүйелердің саны бірден көп бола алмаса да, олар көп деп, және олар ансамбль құрайды деп болжайық. Егер әр мұндай жүйедегі сәйкесінші денелердің координаттары мен жылдмадықтары бірдей болса, барлық бұл жүйелерге фазалық кеңістікте бір нүкте сәйкес келетін еді. Бірақ мұндай ансамбльден көрі әр қайсысындағы координаттар мен жылдамдықтар үлестірілуі өзгеше болып табылатын, ал құрамдарына кіретін объекттер саны бірдей жүйелерден тұратын ансамбльді қарастыру қызық. 6N-өлшемді фазалық кеңістікте мұндай ансамбльге нүктелер бұлты сәйкес келеді. t уақыт мезетінде ансамбльдің берілген жүйесінің фазалық кеңістіктің берілген 6N-өлшемді элементіне түсуінің ықтималдығын

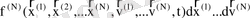
деп белгілейік. f ^(N) -ң мәні координаттары мен жылдамдықтары фазалық көлемнің берілген элементіне түсетін ансамбль жүйелерінің салыстырмалы санын береді. Лиувилль көрсеткендей, бұл шама үшін мына өрнек орындалады:

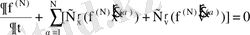
Бұл теңдеу (*) үздіксіздік теңдеуінің 6N-өлшемді фазалық кеңістік үшін жалпылауы болып табылады. Оның түрі Больцманның теңдеуіне де өте ұқсайды, бірақ Лиувилль теідеуі Больцман теңдеуінен әлде-қайда қуатты болып табылады, өйткені одан ешбір болжау мен жуықтау қолданбай, жүйенің барлық орбиталары туралы толық мәліметті алуға болады. Больцман теңдеу жарамды болу үшін, объектер қозғалысы тек баяу өзгеретін гравитациялық өріспен себептелу тиіс болса, Лиувилль теңдеуі тек жүйенің қозғалыс теңдеулерінің үздіксіздігін талап етеді. Әрине, Лиувилль теңдеуін іс жүзінде қолдану айтарлықтай қиыншылықтарға әкеліп соғады, бірақ, оған қарамастан, ол өте пайдалы болып табылады.

Жұлдыздық жүйелердің релаксациясы

Соқтығулар болмағандағы жүйелерде қарқынды деп аталатын релаксация жүреді, ол массалары әр түрлі бөлшектердің орташа жылдамдықтарының теңесуіне әкеледі. Шынайы (соқтығулар бар болғандағы) релаксация бөлшектредің жылдамдықтар бойынша Максвелл үлестіруінің орналасуына әкеледі, бұл жағдайда массалары әр түрлі бөлшектердің орташа энергиялары теңеседі.

Жұлдыздар булануы

Соқтығулар болатын жұлдыздық жүйеде орташа жылдамдықтан әлдеқайда жоғары жылдмадықпен қозғалатын жұлдыздар қашанда да болады (жұлдыздың орташа жылдамдықтан әлдеқайда жоғары жылдмадықты алуының ықтималдығы айтарлықтай болады) . Бұның үш негізгі себебін атап айтуға болады.

Біріншіден, жұлдыздық жүйедегі бөлшектердің (жұлдыздардың немесе галактикалардың) соқтығулары максвелдік үлестірілудің орналасуына әкеледі, бұл үлестіру бойынша жұлдыздардың орташа кинетикалық энергия бірдей болады, демек орта есеппен алғанда жеңіл жұлдыздардың жылдмадығы ауыр жұлдыздар жылдмадығынан көп болады. Екіншіден, Максвелл үлестірілуі бойынша бөлшектердің барлығы бірдей (орташа) энергияға ие болмайды: жүйеде энергиялары орташадан көп те, аз да бөлшектер болады. Үшіншіден, жұптасып соқтығулардан (яғни екі жұлдыздың бір біріне жақындап, энергиямен алмасудан) басқа, үш (не одан да көп) жұлдыздың тығыз әрекеттесуі болуы мүмкін. Мұндай әрекеттесулер әр түрлі нәтижелерге әкеледі. Мысалы, екі жұлдыз гравитация арқылы байланыстырылған, баяу қозғалатын қос жүйеге бірігіп, үшінші жұлдыз байланыс энергияны өзімен бірге әкетіп, жоғары жылдамдықпен алысқа «атылуы» мүмкін.

Жетерліктей жоғары жылдамдыққа ие болған жұлдыздар жүйеден шығып кете (булана) алады. Сөйтіп, соқтығулар жұлдыздардың жүйеден булануына әкеледі. Жұлдыздардың булануына ең көп әкелетін - алыс өтетін жұлдыздармен соқтығулар болады, олар кезінде қарастырылып отырған жұлдызға энергияның аз мөлшерлері беріледі. Сондықтан жоғары жылдамдықпен ұшып шығатын жұлдыздардың салыстырмалы саны аз болады (~ 1/ln N ) , ал жұлдыздардың көбісі кеңістікте жайылып, көлемді галоны құрайды. Ал қалған жұлдыздар (көбісі ол массасы жоғары жұлдыздар болады) өз энергиясын жоғалтып (буланатын жұлдыздарға беріп), керісінше, жүйенің центріне қарай түседі де, тығыздалып тұратын ядроны құрайды. Ақырда, оқшауланған жұлдыздық жүйе жұлдыздарының көбісі буланып, қалдығы релятивтік гравитациялық коллапсқа ұшырау тиіс, яғни жүйенің орталық бөлігі шекті уақыт ішінде «шексіз» тығыздық пен «нольдік» өлшемге дейін сығылу тиіс (немесе қара құрдым түзілуі тиіс) (егер тек жұптасып соқтығулар еске алынса) . Бірақ іс жүзінде солай болмайды. Жақын қашықтықта ұшып жатқан екі жұлдыздың бір біріне тасулық әрекетін еске алғанда, кездескен сол жұлдыздар жай ғана энергияларымен алмаспайтынын, тасулық әрекет нәтижесінде байланысып, тығыз қос жүйеге айнала алатынын көруге болады. Ал қос жұлдыздардың түзілуі жұлдыздық жүйенің оның ядросы сығылу кезеңіндегі эволюциясына елеулі әсер етеді екен. Тығыз қос жүйе басқа жұлдызбен кездескенде, одан да тығыз жүйеге айналады (яғни, оның құрамына кіретін екі жұлдыз бір біріне одан да жақын орналасатын болады, ал олардың гравитациялық байланысы одан да жоғары болады), ал байланыс энергияның айырмасын өзімен кездескен жұлдыз әкетеді. Сөйтіп, тығыз қос жүйе басқа жұлдызбен кездескенде, оған өзінің энергиясының бір бөлігін береді де, оны үдетеді. Және де тығыз қос жұлдыздар әсіресе жұлдыздық жүйенің тығыз ядросында жиі түзіледі, өйткені олар бір біріне тек қана өте аз қашықтыққа жақындаған жұлдыздар арасында «қосылатын» тасулық әрекеттің салдарынан пайда болады, ал мұндай кездесулер жұлдыздар тығыздығы жоғары болғанда жиі болатыны түсінікті. Сөйтіп, жұлдыздық жүйе ядросының тығыздығы артқан сайын жұлдыздар бірі бірімен жиі кездесе бастайды, тығыз қос жүйелердің түзілуі жиілінеді, бұл қос жүйелер жеке жұлдыздарды үдетеді де, олар тығыз аймақтын шығып кетіп, жүйенің шеттеріне қарай кетеді. Жұлдыздық жүйенің газ бұлтымен ұқсасытығын қарастырсақ, қос жұлдыздар бұлтқа сығылуғы бермейтін жылу көзінің ролін атқарады деп айтуға болады. Бұл ұқсастықты одан әрі жалғастыруға болады: газдық шар болып табылатын жұлдыздың тұрақсыздығын қамсыздандыратын (жұлдызды сығылуға жібермейтін) - оның ядросында болатын сутегінің (жеке протондардың) төрт нуклоннан тұратын гелийге айналудың термоядролық реакциялар, және бұл реакциялар жүрісінде шығарылатын байланыс энергиясы.

... жалғасы

Сіз бұл жұмысты біздің қосымшамыз арқылы толығымен тегін көре аласыз.