Хаостық сигналдардың екіөлшемді формасының коэффициенті және мультифракталдық спектр: корреляциялық өлшем және Лежандр түрлендіруі

Пән: Физика
Жұмыс түрі: Реферат
Тегін: Антиплагиат
Көлемі: 5 бет
Таңдаулыға:

Хаостық сигналдардың формасының екіөлшемді коэффициенті

Хаостық сигналдар үшін қисықтардың әр тұрлі формаларын сипаттайтын жалпы сандық сипатын орнатайық. Бұл мақсаттар үшін метрикалық сипаттамалардың (ұзындық, аудандар, көлем) болуы келесі Коши - Буняковскийдың теңсіздігінің орындалуына негізделген деп ескереміз:

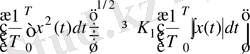немесе 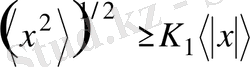, (2. 27)

Мұнда t және T ағымдық және сипаттық мағынаға ие болуы мүмкін . Теңсіздік мына кезінде орындалады

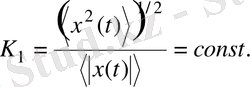(2. 28)

K ₁ шамасы радиофизикада қолданылады және импульсты сигналдар формасының коэффициенті деп аталады [18] .

(2. 28) теңсіздігі кез келген функция x _i (t), x _j (t) , үшін келесі түрде жазылған Гельдеринтегралдық тепе-теңсіздіктен шығады.

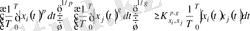. (2. 29)

мұнда p , g - 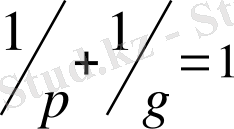, шартын қанағаттандыратын кейбір сандар

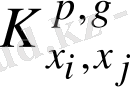-шамасы тұрақты болған кезде (2. 28) теңдігі орындалатын коэффициент:

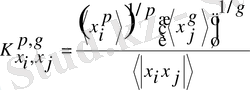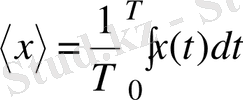, . (2. 30)

(2. 29) интегралы аргументті өсіру барысында Риман әдісі арқылы есептеледі

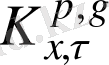сипаты алғаш рет . Ж. Жаңабаев [15] жұмысында енгізілген және хаостық сигналдың біртексіздігін аффинділігін және әр түрлі формаларын сипаттайтын форманың екі өлшемді коэффициенті немесе жалпыланған метрикалық сипаттама деп аталады. Функцияның 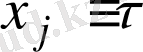түрінде таңдалу мүмкіндігі әрбір зерттелініп отырған импульс үшін бұл құбылыстың сипаттық уақыты екендігімен негізделген.

2. 4 Корреляциялық өлшемділік

Бірдей өлшемді δ ұяшықтарға бөлінген фракталды бетті қарастырайық және кез-келген х ₁ және х ₂ еркін таңдалған екі нүкте фракталды объектіге жататын нүктелер болсын делік. _. Екі нүктеніңде i -ші ұяшықта болу ықтималдығы қанша? Бір нүктенің осы беттің i -ші элементіне түсу ықтималдығы р _i -ге тең. Егер екі нүктенің осы ұяшыққа түсуі байланыссыз оқиғалар деп алсақ, онда оның ықтималдығы 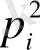-ге тең болады.

Фракталдық бет (q = 2) жабылатын ұяшықтар көлемін кішірейткендегі, статистикалық қосындының өзгерісін қарастырайық. δ-ны кішірейткенде қосынды азаяды, бұдан ол дәрежелік заңға бағынады деп жорамалдауға болады:

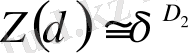, (2. 31)

немесе, эквивалентті, шек

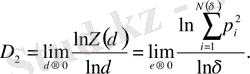(2. 32)

D2 корреляциялық өлшемділік деп аталады.

Dq шамасы жалпы қабылданған мағынасында нақты айтатын болсақ фракталдық өлшемділік емес. Сондықтан көп жағдайда мультифракталды жиынды бейнелеу үшін мультифракталды спектрлік функция f(α) (мультифракталдың сингулярлығының спектрі) қолданылады. Біз f(α) шамасы ℒ жиынындағы біртекті фракталдық ішкі жиынының хаусдорф өлшемділігіне тең екендігін көрсетеміз.

Өзұқсас жиын үшін рi шамасының δ ұяшық өлшеміне тәуелділігі дәрежелік байланыста болады

(2. 33)

мұндағы αi - қандайда бір дәрежелік көрсеткіш (шынында әр-түрлі i ұяшыққа әр-түрлі) . Регулярлы (бірқалыпты) фракталдар үшін αi дәрежелік көрсеткіштер бірдей және D фракталдық өлшемділікке тең

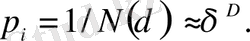(2. 34)

Бұл жағдайда (2. 6. 2) статистикалық қосынды келесі түрге өзгереді

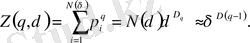(2. 35)

Сондықтан және барлық жалпыланған фракталдық өлшемділіктер Dq=D бұл жағдайда бір-біріне сәйкес келеді және q-ға байланысты емес. Бірақ мультифрактал сияқты күрделі объектілер үшін рi ұяшықтардың толтырылу ықтималдығы бірдей емес және αi дәреже көрсеткіші әр-түрлі. Көп кездесетін жағдайдың бірі - осы мәндер қандайда бір (αmin, αmax) жабық интервалды толтырады және

. (2. 36)

Осы α-ның шектік мәндерімен τ(q) функциясының туындысы мәндерінің арасындағы байланысты, атап айтқанда q→± 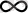ұмтылғандағы туындының шектік мәндерін қарастырайық. Егер біз q→ 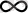мәнін алсақ, (2. 34) тендеудегі i бойынша қосындыға, максималды рmax толықтыру ықтималдығымен сипатталатын тек ішінде көп нүктелер шоғырланған ұяшықтар көп үлес береді. Қосындыда тек осындай (саны Nmax) ұяшықтарды қалдыра отырып, (2. 6. 4) теңдеудің алымы Nmax 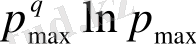, ал бөлімі Nmax 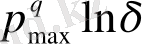екендігін көреміз. Соңында, 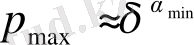екенін ескерсек, ізделіп отырған туындының шегі αmin -ға тең болады. Сол сияқты, q→- 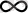, жағдайда (2. 34) теңдеудегі қосындыны үшін рmin ықтималдықпен сипатталатын тек аз нүтелері бар ұяшықтарды ескеру қажет. Бұл жағдайда 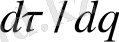туындысы αmax мәніне ұмтылатыны анық.

Сонымен біз маңызды қорытындыға келеміз:

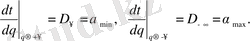(2. 37)

яғни мүмкін болатын α интервалы, q→± 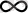жағдайда жалпыланған фракталдық өлшемділіктің Dq шектік мәндерімен анықталады.

Енді αi-ның әр-түрлі мәндерінің таралу ықтималдылықтарына тоқталайық. Айталық αi -нің α дан α + dα-ға дейінгі интервалда болу ықтималдылығы n(α) dα болсын. Басқаша айтқанда n(α) dα осы интервалда жатқан, αi мен pi мәндері бірдей, салыстырмалы ұяшықтар саны i. αi әр-түрлі мәні тек D мен ғана бейнеленетін ықтималдықпен ғана кездеспей, ол әр-түрлі (α-ға байланысты) f(α) дәрежелік көрсеткіш мәнімен сипатталады:

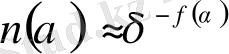. (2. 38)