Күрделі және күшті біртекті емес сигналдардың энтропиясы, эволюциялық параметрі және фракталдық ақпараттық сипаттамалары


Энтропия және эволюция параметрі
Күрделі-кезектесетін, күшті біртекті емес сигналдардың сандық сипаттамасын орнату қажет. Сигнал күрделігінің белгілі сипаттамасы
 - база келесі түрде анықталады:
- база келесі түрде анықталады:
 , (1. 5)
, (1. 5)


 (1. 6)
(1. 6)
мұнда
 - корреляциялық функция,
- корреляциялық функция,
 - қуаттылық спектрі,
- қуаттылық спектрі,
 -
жиілік жуықтарының тиімді ені,
-
жиілік жуықтарының тиімді ені,
 - корреляцияның тиімді уақыты.
- корреляцияның тиімді уақыты.
Толқын үдерістерінде белгісіздік шамасы ретінде (1. 5) мәнін пайдаланудың мағынасы фазалық кеңістіктің минималды ұяшығы бар дегенге сай келеді (квантты физикадағы белгісіздің қатынасының аналогиясы) . Алайда корреляциялық функция және оған тиісті қуаттылық спектрі энергетикалық сипаттама болып табылады, олар ауытқу фазасы, пішіні туралы информацияны ескермейді. Ізделінуші күрделілік шамасын тікелей
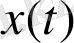 жүзеге асыру арқылы анықтауға болады. Бастапқыда біз күрделіліктің таза метрикалық сипаттамасын қарастырамыз, тиісті топологиялық (информация-энтропиялық) сипаттаманы жеке талқылайтын боламыз.
жүзеге асыру арқылы анықтауға болады. Бастапқыда біз күрделіліктің таза метрикалық сипаттамасын қарастырамыз, тиісті топологиялық (информация-энтропиялық) сипаттаманы жеке талқылайтын боламыз.
Метрикалық сипаттамаларының (ұзындық, аудан, көлем)
 кез келген функциялары үшін Гёлдер интегралды теңсіздігін орындау керек,
кез келген функциялары үшін Гёлдер интегралды теңсіздігін орындау керек,
 :
:
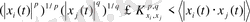 ,
,
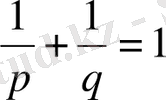 , (1. 7)
, (1. 7)
мұнда теңдік тұрақты
 жағдайында орындалады. Физикалық қосымшаларда уақыты бойынша орташаланған
жағдайында орындалады. Физикалық қосымшаларда уақыты бойынша орташаланған
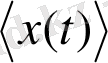 пайдалануға болады.
пайдалануға болады.
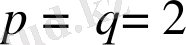 жағдайында ізделінуші сипаттама
жағдайында ізделінуші сипаттама
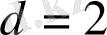 топологиялық өлшемділігі бар евклидтік беткейде анықталады. Егер
топологиялық өлшемділігі бар евклидтік беткейде анықталады. Егер
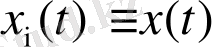 ,
,
 ,
,
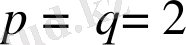 болса, онда біз
болса, онда біз
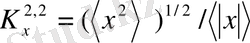 -радиофизикада пайдаланылатын сигнал пішінінің коэффициентін аламыз.
-радиофизикада пайдаланылатын сигнал пішінінің коэффициентін аламыз.
Егер
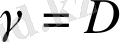 ,
,
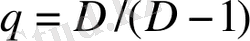 деп қабылдасақ, өзара күрделілік сипаттамасын
деп қабылдасақ, өзара күрделілік сипаттамасын
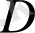 фракталды өлшемділігі бар жиында анықтауға болады. Мұнда ықтимал
фракталды өлшемділігі бар жиында анықтауға болады. Мұнда ықтимал
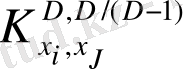 асимптотикалық мәнін итерациялық жолмен табуға болады:
асимптотикалық мәнін итерациялық жолмен табуға болады:
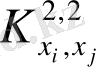 фракталды шаманың бастапқы мәні ретінде қабылдауға болады, содан кейін фракталды өлшемділікті анықтау формуласы бойынша
фракталды шаманың бастапқы мәні ретінде қабылдауға болады, содан кейін фракталды өлшемділікті анықтау формуласы бойынша
 -ны табу (алғашқы жуысу нәтижесі) және
-ны табу (алғашқы жуысу нәтижесі) және
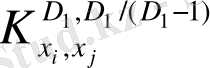 пайдалануға болады және т. б.
пайдалануға болады және т. б.
(1. 7) формуласында теңдік жағдайында
 (1. 8)
(1. 8)
Екі ерікті функция үшін оң жақтағы мәннің күрделілік (біртексіздік) шамасының минималды мәнін аламыз. (1. 26) формуласы орталықтанбаған автокоррелляцияның кері коэффицентінен ерекшеленеді: функция туындысының модулі орташаланады,
 мүмкіндігі ескеріледі.
мүмкіндігі ескеріледі.
Кезектесетін функциялар (
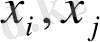 ) бір-біріне қатысты және (
) бір-біріне қатысты және (
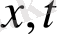 ) аргументке қатысты күшті біртекті емес болып табылады. Ұқсастық, масштабты инварианттылық теориясы терминдерінде кездестестірілетін сигналдар ұқсас емес, аффиндік болып табылады: өзұқсас қасиеттеріне ие емес, өзаффиндік болуы мүмкін. (1. 8) формуласында
) аргументке қатысты күшті біртекті емес болып табылады. Ұқсастық, масштабты инварианттылық теориясы терминдерінде кездестестірілетін сигналдар ұқсас емес, аффиндік болып табылады: өзұқсас қасиеттеріне ие емес, өзаффиндік болуы мүмкін. (1. 8) формуласында
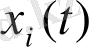 ,
,
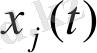 функцияларының еріктілігіне орай, осындай теңсіздікті ескеру үшін, біз айнымалыны анықтайтын реттілік параметрі ретінде олардың бірін таңдап алуымызға болады. Егер бізді уақыт бойынша эволюция
функцияларының еріктілігіне орай, осындай теңсіздікті ескеру үшін, біз айнымалыны анықтайтын реттілік параметрі ретінде олардың бірін таңдап алуымызға болады. Егер бізді уақыт бойынша эволюция
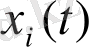 қызықтыратын болса, онда
қызықтыратын болса, онда
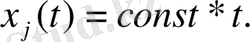 таңдауымызға болады. Сөйтіп, (1. 8) мәні
таңдауымызға болады. Сөйтіп, (1. 8) мәні
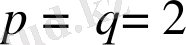 жағдайында келесі түрге ие болады:
жағдайында келесі түрге ие болады:
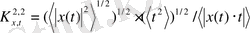 . (1. 9)
. (1. 9)
Физикалық үдерістерді сипаттау үшін, келесі мән қызығушылық тудырады:
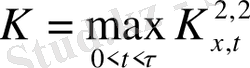 , (1. 10)
, (1. 10)
мұнда
 -
-
 максимумға жететін уақыт.
максимумға жететін уақыт.
(1. 10) мәнін реттіліктің эволюциялық параметрі деп атаймыз. Осы параметр өлшемсіз уақыт мағынасына ие және динамикалық жүйелердің дискретті көріністері қадамының пропорционал нөмірі болып табылады.
1. 4. 1 Ашық жүйелер эволюциясының әмбебап энтропиялық заңдылықтары
Ашық жүйелер физикасында өзұқсас және өзаффиндік режімдерді пайдаланумен байланысты мәселелер маңызды болып табылады. Егер айнымалыларды анықтайтын сан бірліктен көп болса және осы айнымалылар бойынша ұқсас коэфиценттер түрліше болса, фракталды объект өзафиндік болып табылады. Егер фракталды объектінің иерархиялық бөліктері барлық айнымалылар бойынша бірдей ұқсас коэффиценттерге ие болса, объект өзұқсас деп аталады. З. Ж. Жаңабаевтың [3] жұмысында информациямен энтропияны жүзеге асыру ықтималдылығы тығыздығының жылжымайтын нүктелер түріндегі (
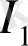 ) өзаффинділік пен (
) өзаффинділік пен (
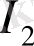 ) өзұқсастың информация-энтропиялық критерийлері анықталды:
) өзұқсастың информация-энтропиялық критерийлері анықталды:
,
;
,
. (1. 11)
Соңғы жылдары жаңа жалпылама статистикалық механика дамып келеді, оны Цаллис статистикасы деп немесе Гиббстың жалған канондық статистикасы деп атауға болады [5] . Осындай теориялардың негізін келесі түрдегі экспоненциалды функцияны пайдалану құрайды:
 (1. 12)
(1. 12)
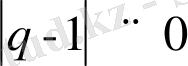 шегінде біз Гиббс канондық үлестіруін сипаттайтын кәдімгі
шегінде біз Гиббс канондық үлестіруін сипаттайтын кәдімгі
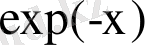 функциясын аламыз.
функциясын аламыз.
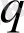 параметрі бірлігінен айырмашылығы, жүйенің статистикалық теңсіздігін, біртекті еместігін сипаттайды. Оңайлау болу үшін біз бұдан әрі
параметрі бірлігінен айырмашылығы, жүйенің статистикалық теңсіздігін, біртекті еместігін сипаттайды. Оңайлау болу үшін біз бұдан әрі
 орнына
орнына
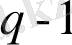 мәнін пайдаланамыз, қажет болған жағдайда ізделінетін физикалық шаманың оң белгісін таңдаймыз.
мәнін пайдаланамыз, қажет болған жағдайда ізделінетін физикалық шаманың оң белгісін таңдаймыз.
(1. 12) мәнін пайдалана отырып,
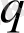 информациялық энтропиядан - тепе-тең емес жүйенің күрделігінің, белгісіздігінің бірден-бір шарасына тәуелділікті анықтаймыз.
информациялық энтропиядан - тепе-тең емес жүйенің күрделігінің, белгісіздігінің бірден-бір шарасына тәуелділікті анықтаймыз.
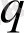 параметрімен сипатталатын жалған үдеріс үшін, информацияны келесі түрде анықтаймыз:
параметрімен сипатталатын жалған үдеріс үшін, информацияны келесі түрде анықтаймыз:
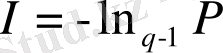 . (1. 13)
. (1. 13)
Осыдан келіп ықтималдылықты информация функциясы ретінде көрсетеміз:
 . (1. 14)
. (1. 14)
Информацияны жүзеге асыру ықтималдығы үлестіруінің тығыздық функциясы
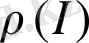 былай анықталады:
былай анықталады:
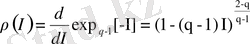 . (1. 15)
. (1. 15)
Энтропия информацияның орташа мәні ретінде анықталады:
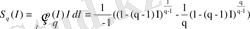 . (1. 16)
. (1. 16)
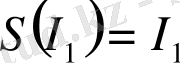 және
және
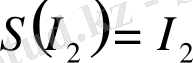 өзұқсас мәндерін жылжымайтын көрініс нүктелері ретінде табамыз:
өзұқсас мәндерін жылжымайтын көрініс нүктелері ретінде табамыз:
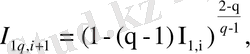 (1. 17)
(1. 17)
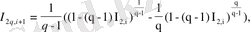 (1. 18)
(1. 18)

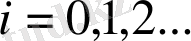 .
.
Сөйтіп,
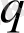 параметрі информация және информациялық энтропия мәндері арқылы өзұқсас және өзаффиндік күйінен ауытқуын сипаттай алады.
параметрі информация және информациялық энтропия мәндері арқылы өзұқсас және өзаффиндік күйінен ауытқуын сипаттай алады.
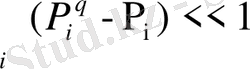 , (1. 19)
, (1. 19)
Шарты жағдайында (1. 12) формуласымен анықталатын Реньи энтропиясымен сәйкес келеді:
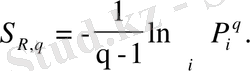 (1. 20)
(1. 20)
Біртексіздік параметрін [6] формуласымен анықтауға болады:
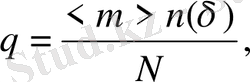 (1. 21)
(1. 21)
- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz