Ашық жүйелердің ақпараттық-энтропиялық критерийлері мен өзұқсас импульстердің фракталдық метрикалық сипаттамасы


Жұмыс түрі: Реферат
Тегін: Антиплагиат
Көлемі: 5 бет
Таңдаулыға:
Жалпы қабылданған терминологияға сәйкес I i информациясы, P i ықтималдыққа ие құрылым пайда болғанда (жоғалғанда) (2) формуламен есептелінеді және келесі түрде табылады:
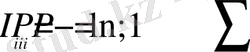 , (16)
, (16)
ал оның орта мәні - информациялық энтропия (8) -өрнекпен анықталады.
Әртүрлі иерархиялық деңгейлердегі өзұқсастық, өзқауымдық жүйелердің әмбебаптық қасиеттерінің бірі болып табылады. Олардың сипаттамасының масштабты инварианттылығы информацияның үздіксіз мәндерін қабылдауға мүмкіндік береді. Ал информацияны анықтаушы физикалық шама ретінде қабылдауға болады. Мұндай жағдайлар, алдымен күй функцияларының арасында (мысалы энергия мен энтропияның арасында) бірмәнді емес байланыс орнайтын күшті бейсызық динамикалы-информациялық жүйелерге (турбулентті орта, биологиялық объектілер т. б. ) қатысты.
Сондықтан, информацияның байқалу ықтималдылығы жөнінде айтуға болады:
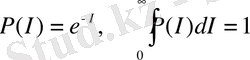 . (17)
. (17)
P ( I ) ықтималдықты f ( I ) ықтималдықтың таралу тығыздығының функциясы арқылы жазсақ:
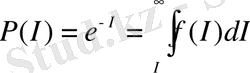 , (18)
, (18)
мұндағы интеграл шектері
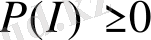 аймаққа сәйкес келеді. Демек,
аймаққа сәйкес келеді. Демек,
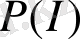 - информацияның байқалу ықтималдық функциясы
- информацияның байқалу ықтималдық функциясы
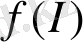 - ықтималдықтың таралу тығыздығының функциясымен сәйкес келеді. Информация күрделі жүйелердің барлық иерархиялық деңгейлерінің жалпы және толық сипаттамасы болып табылады: жүйенің бір бөлігі жалпы жүйе туралы мәліметті қамтиды.
- ықтималдықтың таралу тығыздығының функциясымен сәйкес келеді. Информация күрделі жүйелердің барлық иерархиялық деңгейлерінің жалпы және толық сипаттамасы болып табылады: жүйенің бір бөлігі жалпы жүйе туралы мәліметті қамтиды.
(18) формуланы ескере отырып, өзұқсас жүйелердің информациялық энтропиясын келесі түрде жазамыз:
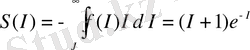 . (19)
. (19)
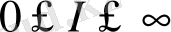 үшін
үшін
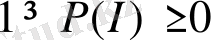 және
және
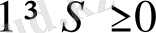 болады.
болады.
Өзқауымдық жүйенің өзұқсастығы қандай да бір сипаттамалы
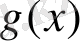 функциясының мына функционалды теңдеуге сәйкестігімен сипатталады:
функциясының мына функционалды теңдеуге сәйкестігімен сипатталады:
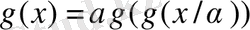 , (20)
, (20)
мұндағы
α
- масштабты көбейткіш. Кез-келген үздіксіз функция өзінің қозғалмайтын нүктесінде (20) теңдеуді қанағаттандырады. Сипаттамалық функция ретінде
f
(
I
) - ықтималдық тығыздығын және
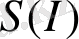 - информациялық энтропияны қабылдап, олардың қозғалмайтын нүктелерін табайық:
- информациялық энтропияны қабылдап, олардың қозғалмайтын нүктелерін табайық:
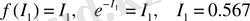 , (21)
, (21)
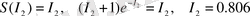 . (22)
. (22)
Бұл қозғалмайтын нүктелер бірмәнді орнықты, себебі олар, сонымен қатар, информацияның
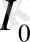 кез-келген бастапқы мәніне сай шексіз бейнелеудің шегі болып табылады:
кез-келген бастапқы мәніне сай шексіз бейнелеудің шегі болып табылады:
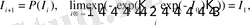 (23)
(23)
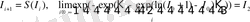 . (24)
. (24)
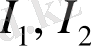 сандарының мағынасын әртүрлі түсіндіруге болады. Олардың ішіндегі ең әмбебабы - Фибоначчи санын (жүйенің динамикалық өлшемі - «алтын қима») қолдану аймағының кеңейуі.
сандарының мағынасын әртүрлі түсіндіруге болады. Олардың ішіндегі ең әмбебабы - Фибоначчи санын (жүйенің динамикалық өлшемі - «алтын қима») қолдану аймағының кеңейуі.
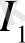 саны информациялық (локальді) сипаттауына, ал
саны информациялық (локальді) сипаттауына, ал
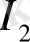 саны күрделі жүйені энтропиялық (орталанған) сипаттауға сәйкес келеді.
саны күрделі жүйені энтропиялық (орталанған) сипаттауға сәйкес келеді.
 болса (22) -ден (21) шығады,
болса (22) -ден (21) шығады,
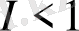 бойынша экспонентаны жіктеудің бірінші мүшесін ескерсек, онда (22) -ден
бойынша экспонентаны жіктеудің бірінші мүшесін ескерсек, онда (22) -ден
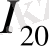 - Фибоначчи саны үшін теңдеу аламыз:
- Фибоначчи саны үшін теңдеу аламыз:
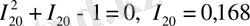 , (25)
, (25)
(21) теңдеуден I - I 10 = I 10 , I 10 = 0, 5.
Сонымен, тәжірибеде күрделі жүйенің өзқауым күйі S ∈[ I 20 I 2 ] жағдайда, қарапайым жүйенің өзұқсас жағдай I ∈[ I 10 , I 1 ] болғанда байқалуы тиіс.
Төменде (21), (22) тәуелділіктерді тұрғызуға арналған бағдарлама және сплайн интерполяцияның көмегімен тұрғызылған график келтірілген (3-сурет) .
% Ықтималдық тығыздығының және энтропияның информациядан тәуелділігін тұрғызу бағдарламасының листингі
clear;
N=12;
I1(1) = 0;
for i1 = 1:N
I1(i1+1) = exp(-I1(i1) ) ;
end;
i1 = 0:N;
i1s = 0:0. 1:N;
I1s= spline(i1, I1, i1s) ;
%
I2(1) = 0;
for i2 = 1:N
I2(i2+1) = (I2(i2) +1) *exp(-I2(i2) ) ;
end;
i2 = 0:N;
i2s = 0:0. 1:N;
I2s= spline(i2, I2, i2s) ;
plot(i1, I1, 'kx', i1s, I1s, 'k', …
i1s, 0. 567, 'k-') ;
hold on;
plot(i2, I2, 'kx', i2s, I2s, 'k', …
i2s, 0. 806, 'k-') ;
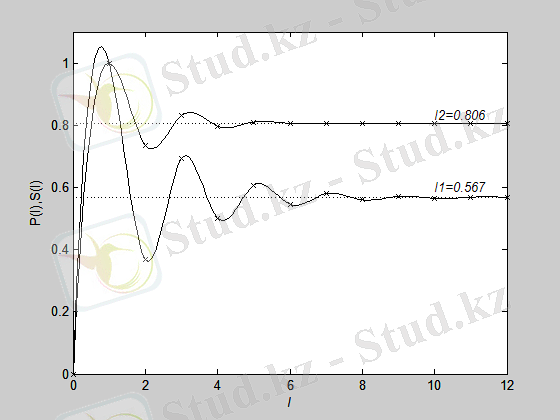
3-сурет. Информация және энтропияның сипаттық уақыт бойынша өзгерісі
I 1 , I 2 сандарының мағынасын жалпылама пайымдаулармен толығырақ ашуға болады. Шеннон бойынша Y берілген кездегі Х шамасы туралы информация шартсыз және шартты энтропиялардың айырымы ретінде анықталады:
S ( X ) - S ( X / Y ) = I ( X ) > 0. (26)
S ( X ) шамасын «Физикалық хаостың» энтропиясының анықталмағандығының нормасы ретінде қабылдап, (26) -ны мына түрде жазамыз:
I + S = 1, (27)
мұндағы I - анықталғандықтың салыстырмалы өлшемі (информация), S - қандайда бір Х сипаттасы бойынша жүйе туралы анықталмағандықтың салыстырмалы өлшемі (энтропиясы) . Жалпы мағынада (27) өрнек кез-келген табиғаттың күрделі жүйелерін өзара байланысқан альтернативті сипаттамаларын байланыстырады: тәртіп және хаос, симметрия және асимметрия, рационалды және иррационалды, детерминизм және индетерминизм және т. б. Альтернативті сипаттамалардың үйлесімі олардың салыстырмалы өлшемінің өзгеруінің пропорционалдылығын болжайды:
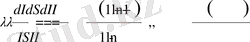 (28)
(28)
мұнда I , S өлшем бірліктерін таңдау еркіндігі мүмкін болғандықтан интегралдау тұрақтысы нөлге тең деп алынған. Дербес жағдайда λ параметріне және I айнымалысына айқын мағына беретін
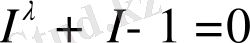 (29)
(29)
алгебралық теңдеуі (28) формулаға эквивалентті. М. Фейгенбаум орнатқан табиғи құбылыстардың әмбебап даму заңдылығының периодты екі еселенуінің бифуркациясын негізге алайық. Жүйенің даму деңгейінің иерархиялық күрделілігін ретіне n- ге сәйкестендіріп, λ = 2 n деп қарастырайық. n = 0, λ = 1 жүйенің статикалық күйіне сәйкес келеді және (29) -дан I = S екені шығады. Динамикалық жүйенің бірінші иерархиялық даму деңгейі ( n = 1, λ = 2) Фибоначчи ( I 3 = 0. 618) санына тең сипаттамалардың пропорциясымен анықталады. Статикалық және динамикалық күйлердің (құрылымның және стохастиканың бастауы) арасында I 1 саны арқылы сипатталатын жүйенің информациялық күйі жүзеге асады. λ =1. 5 деп алып, (29) -дан I = 0. 57 ≈ I 1 болатындығын көреміз. Ли-Йорктің «үш период хаосты білдіреді» атты теоремасы бойынша n = 3 жағдай ішкі тәртібі бар ең күрделі статистикалық күйді I 2 энтропия функциясының қозғалмайтын нүктесімен сипаттайды. λ = 2 3 = 8 үшін (29) -теңдеудің шешімі I = 0. 811 ≈ I 2 болып табылады.
Импульстердің информациялы-энтропиялық сипаттамаларыШекті уақыт аралығында бақыланатын сигналдың (импульстің) ұзақтығы бірдей болсада, оның формасы әртүрлі күрделі қисықтар болуы мүмкін: мейлінше хаосты, өзұқсас құрылымы бар фракталды, алмасу құрылымды және т. б. Күрделі сипаттамаларды өлшеу әрқашан белгілі анықталмағандықпен орындалады. Объектіні статистикалық сипаттау кезінде анықталмағандықтың толығырақ және әмбебап өлшемі жоғарыда көрсетілген информациялық энтропия болып табылады.
Импульстің форма коэффициенттері . Ииформациялық энтропия метрикалық және топологиялық сипаттама болып табылады. Оның заңдылықтарын мөлшерлі түрде сипаттау үшін басқа, мысалы, таза метрикалық сипаттаманы қолдану қажет. Бұл мақсат үшін жекелеген импульстердің формаларының айырмашылығын бірмәнді суреттейтін жалпы метрикалық сипаттама тағайындайық. Метрикалық сипаттамалардың (ұзындық, аудан, көлемнің) болуы Коши-Буняков теңсіздігінің орындалуынан шығады:
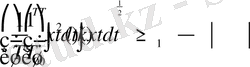 или
или
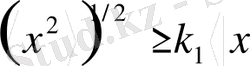 , (30)
, (30)
мұндағы
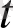 және
және
 өтпелі және сипаттамалы уақыт деген мағынаны білдіреді.
өтпелі және сипаттамалы уақыт деген мағынаны білдіреді.
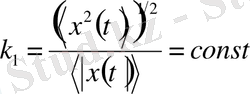 (31)
(31)
болғанда ғана теңдік орындалады. k 1 шамасы радиофизикада қолданылады және ол импульстік сигнал формаларының коэффициенті деп аталады.
... жалғасы- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz