Алгебра, геометрия және логиканың таңдаулы мәселелері пәнінен емтихан сұрақтары

Пән: Математика, Геометрия
Жұмыс түрі: Материал
Тегін: Антиплагиат
Көлемі: 13 бет
Таңдаулыға:

Алгебра, геометрия және логиканың таңдаулы мәселелері пәнінен емтихан сұрақтары:
Ньютон биномы және оған байланысты формулалар.
Бином сөзі француз тілден аударғанда алгебралық екі мүше ұғымын білдіреді.
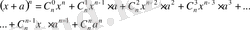(1)
теңдеу Ньютон биномының формуласы. Қысқаша былай беруге болады:
.
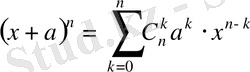Ньютон биномының формуласындағы коэффициенттерді биномдық коэффициент деп атайды.
Ньютон биномының қасиеттері:
Қосылғыштар санының бином дәреже көрсеткішінен біреуі артық, яғни дәреже n болса, қосылғыштар саны (n+1);
х-тің дәреже көрсеткіші n-нен нөлге дейін кемиді, ал а-ның дәреже көрсеткіші нөлден n-ге дейін өседі. Әр қосылғыштың дәреже көрсеткіштерінің қосындысы биномның дәреже көрсеткішіне тең.
Қосылғыштардың коэффициенттері терулер санының қасиетіне байланысты анықталады, яғни жіктелудің басы мен соңынан бірдей қашықтықта тұрған қосылғыштар коэффициенттері өзара тең болады;
Биномның кез келген мүшесі формуласымен анықталады.
Егер х=а=1болса, онда

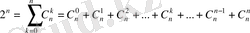
яғни бином мүшелерінің коэффициенттерінің қосындысы 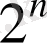дәрежесіне тең.
Егер бином дәреже көрсеткіші тақ натурал сан болса, онда жіктелу қосылғыштарының саны жұп болады, ал егер бином дәреже көрсеткіші жұп сан болса, онда жіктеу қосылғыштарының саны тақ болады;
Коэффициенттері ең үлкен қосылғыштар биномның орта мүшелері деп аталады.
Ньютон биномына қатысты формулалар:
Терулер .
Алмастырула .
Орналастырулар .

Безу теоремасы.
Теорема. 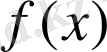көпмүшелігі х-с екі мүшелігіне бөліну үшін 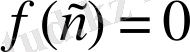болуықажетті және жеткілікті.
Салдар.
А саны сонда тек сонда, егер p(x) қалдықсыз х-а-ға бөлінсе p(x) көпмүшелігінің түбірі болады (осыдан Р(х) көпмүшелігінің түбірлер жиыны сәйкес Р(х)=0 теңдеуінің шешімдер жиынымен бірдей).
Бүтін коэффициентті көпмүшеліктің бос мүшесі көпмүшеліктің кез келген бүтін түбіріне қалдықсыз бөлінеді (егер жоғарыкоэффициентті бір болса, онда барлық рационал түбірлері де бүтін болады).
α - бүтін коэффициентті А(х) келтірілген көпмүшеліктің бүтін түбірі болсын, онда кез келген бүтін k саны үшін А(к) саны α-к санына бөлінеді.

Горнер схемасы.
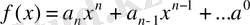көпмүшелігін х-с екі мүшелігіне бөлеміз. Қалдықпен бөлу теоремасы бойынша 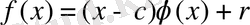теңдігі орындалады, мұндағы с, rϵK, ал .

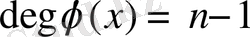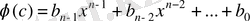
Келесі таблица 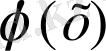көпмүшелігінң коэффициенттері мен r қалдықты есептеудің тиімді әдісін көрсетеді. Оны Горнер схемасы деп атайды.

...

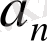
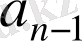
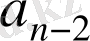
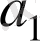
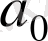
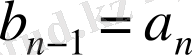
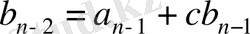
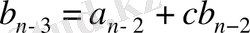
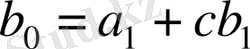
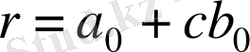
Мысалы., 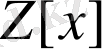сақинасында 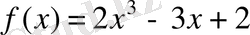көпмүшелігін х+2 көпмүшелігіне қалдықпен бөл.
Шешуі. 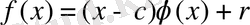, мұндағы 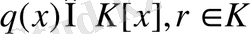. 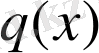көпмүшелігінің коэффициенттері мен r қалдықты Горнер схемасы бойынша табуға болады:
Мұнда х-с=х+2, сондықтан с=-2. Онда Горнер схемасы келесі түрде жазылады:

2
0
-3
2
-2
2
-4
5
-8
Жауабы: 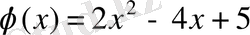, r=-8.

Евклидтік геометрия.
Евклидтік геометрия - алғаш рет Евклидтің (б.з.б. 330 - 275) "Негіздерінде" мазмұндалған аксиомалар жүйесіне негізделген геометриялық теория. Осы геометрияның аксиомалары 5 топтан, 6 негізгі (анықтама берілмейтін) түсініктерден құралған. Бұлар -- үш түрлі объектілер: нүкте, түзу сызық, жазықтық және үш түрлі қатынастар "тиісті", "аралығында", "қозғалыс".
Тиесілік (тиістілік) аксиомалары
Әрбір екі нүкте арқылы тек бір ғана түзу сызық сызуға болады.
Бір түзу сызықтың бойында жатпайтын ең кемі үш нүкте болғанмен, әрбір түзу сызықтың бойында ең кемі екі нүкте жатады.
Бір түзу сызықтың бойында жатпайтын үш нүкте арқылы тек бір ғана жазықтық жүргізіледі.
Бір жазықтықта жатпайтын төрт нүкте болғанмен әрбір жазықтықта үш нүкте жатады.
Егер берілген түзу сызықтың екі нүктесі берілген жазықтықта жататын болса, онда түзу сызықтың өзі де осы жазықтықта жатады.
Егер екі жазықтықтың ортақ нүктесі болса, онда олардың тағы бір ортақ нүктесі болады (олай болса, ортақ түзу сызығы болады).
Реттілік аксиомалары
Егер нүктесі және нүктелері аралығында жатса, онда осы үш нүкте бір түзу сызықтың бойында жатады.
Әрбір , нүктелері үшін мынадай нүктесі болады, нүктесі мен нүктелері аралығында жатады.
Түзу сызықтың үш нүктесінің тек біреуі ғана екі нүкте аралығында жатады.
Паш аксиомасы: егер түзу сызық үшбұрыштың бір қабырғасын қиып өтетін болса, онда ол түзу сызық әлгі үшбұрыштың екінші қабырғасын да қиып өтеді немесе оның төбесі арқылы өтеді ( кесіндісі және нүктелері аралығындағы нүктелердің жиыны ретінде анықталады; үшбұрыштың кабырғалары да осылайша анықталады).
Жылжу (қозғалу) аксиомалары
Жылжыту (қозғалту) нүктелердің түзу сызықтарға және жазықтықтарға тиесілігін (тиістілігін) сақтай отырып нүктелерді нүктелерге, түзу сызықтарды түзу сызықтарға, жазықтықтарды жазықтықтарға сәйкес қояды.
Бірінен соң екіншісі кайталанатын екі жылжыту (қозғалту) тағы бір жылжыту тудырады және әрбір жылжытуға кері жылжыту болады.
Егер мен нүктелері және осы нүктелер басталатын бір шеті шектелген және жарты түзу сызықтар орналасқан (альфа) және (бета) жарты жазықтықтары берілген болса, онда -ны -ға ауыстыратын жылжыту да болады.
Үздіксіздік аксиомалары
Архимед аксиомасы: Кез келген кесіндіні оның үстіне одан қысқа болатын кесіндісін кажет болғанша қайталап салып, әлгі кесіндісінен артып кететін (ұзын) кесінді салуға болады
(,) кесіндіні қайталап салу жылжыту (немесе қозғалту) арқылы жүзеге асырылады.
Кантор аксиомасы. Егер шексіз рет кайталанып беттестіре салынған кесінділер тізбегі берілсе, онда бүкіл кесінділеріне тиесілі (тиісті) бір ғана нүктесі болады.
Параллелдік аксиомасы
Жазықтықта берілген түзуден тысқары жатқан нүкте арқылы әлгі түзумен қиылысатын бір ғана түзу сызуға болады, яғни берілген түзуге параллель болатын бір ғана түзу сызылады.
Евклид геометриясының өзге түсініктері осы негізгі ұғымдар арқылы анықталған. Егер Евклидтік геометрияның параллелдік аксиомасы ауыстырылатын болса, онда жаңадан пайда болған аксиомалар жүйесі (Лобачевскийдің геометриясының аксиомалар жүйесі) қайшылыққа ұшырамайды. Өйткені параллелдік аксиомасы өзге аксиомаларға тәуелсіз

Элементар геометрия курсының мазмұн
Геометрия - ең ежелгі ғылымдардың бірі. Геометрия сөзі жер өлшеу сөзінен шыққан. Элементар геометрия курсы планиметрия және стереометрия болып екіге бөлінеді.
Планиметрия (лат. planum -- жазықтық және ...метрия) -- элементар геометрияның жазықтықта жатқан фигуралардың қасиеттерін зерттейтін бөлімі. Әдетте Планиметрия деп орта мектепте оқылатын геометрия курсының бір бөлімі түсініледі. Планиметрияның мазмұнын ертедегі грек ғалымы Евклид айқындаған және оның баяндалу тәсілін жасаған. Мектеп курсындағы планиметроның мазмұны: жазықтықтағы түзулер мен бұрыштар, үшбұрыштар, көпбұрыштар және төртбұрыштар, шеңбер, жазықтықтағы векторлар, жазықтықтағы фигураларды түрлендіру.
Стереометрия (гр. stereo - кеңістік, metreo - өлшеймін)[1] - элементар геометрияның кеңістіктегі фигуралардың қасиеттерін зерттейтін бөлімі. Бұл бөлімде мыналар оқытылады:
Кеңістіктегі түзулер мен жазықтықтар; кеңістіктегі бұрыштар; көпжақтар (призма, пирамида т.б); айналу денелері (цилиндр, конус; шар т.б); көпжақтар мен айналу фигураларының комбинациялары.

2. Математика есептерін шешуді оқытуды ұйымдастырудың теориялық негіздері пәнінен емтихан сұрақтары:
Есептердің классификациясы.
Оқушының оқыту үрдісінде бір ғана есеппен емес, олардың жиынтығымен жұмыс істеуге тура келеді. Есептер жиынтығын талдау оларды сипаттауды талап етеді. Соңғы уақыттар да есептерді классификациялау проблемасы психологтардың, әдіскерлердің басты назарына ілінді. Есептерді классификациялауға арналған әртүрлі зерттеулерді талдау бұл проблеманы шешудің әр түрлі жолдары бар екенін көрсетті. Кейбір авторлар оларды төмендегіше а) дәлелдеуге арналған есептер; б) құруға арналған есептер; в) ізделіндіні табуға арналған есептерге бөле отырып, есеп талабының сипатын негізге алады. басқалары есеп шартының анықтығына қарап сипаттауды ұсынады (А.Фуше, Л.М.Фридман, Л.Л.Гурова т.б). Есептің проблемалық деңгейіне қарай сипаттауға талпыныс жасағандар болды (У.Рейтман, Ю.Н.Колягин). есептерді геометриялық қайта өзгертулерге жинақтау, векторлық әдіске есептер және т.б. ұсынылды. Есептерді қарапайым және күрделі есептер деп бөлді. Одан басқа есептерді шығармашылық және шығармашылық емес, стандартты және стандартты емес, теориялық және практикалық, ауызша және жазбаша т.б. түрлерге ажыратады.
В.А.Онищук жаттығуларды дидактикалық деңгейде жүйлеуге талпыныс жасады. Автор біліктілік меңгерудің төмендегі кезеңдерін көрсетті. 1) негізгі білімді өзектендіру; 2) білімді меңгеру; 3) білімді алғаш қолдану; 4) стандартты жағдайларда дағдыны иелену; 5) білім, білік, дағдыны шығармашылықпен беру.
Есептер классификациясында есептің әр түрлі жақтарын бейнелейтін әр түрлі әдістер байқалады. Бұл есептің көп аспектілігін, оларды оқыту үрдісінде әр түрлі жақтармен көріну қабілетін тағыда нақтылайды. Әдістердің әр алуандығы есептің шынайы көпжақтылығын бейнелейді.
Есептер шығаруға үйрету.
Есеп шығару қанддай мақсатқа бағытталса да мұғалімнің басты міндеті оқушылардың есеп шығару тәжірибесін молайту, оларды есеп шығаруға үйрету болуы тиіс. Мұғалім сұрақ-жауап арқылы ақыл-кеңес бере отырып, оқушының есеп шығарудың әр қилы сырына үйрете алады.
Есеп шығаруға бағыт-бағдар беретін ғылыми-әдістемелік әдебиеттреге шолу жасай отырып, қандай да болмасын есепті шығаруды негізгі төрт кезеңге бөлуге болады:
Есептің шарты мен талабын терең түсіну;
Есепті шығарудың жоспарын құру;
Жоспарды жүзеге асыру;
Есепті тиянақтау.
Көрсетілген кезеңдерге байланысты негізгі мәселелер төңірегінде кеңес берелік.
Есепті дұрыс түсініп алмай, оны әрі қарай жалғастыру мүмкін емес. Мүмкіндігінше есеп шартында артық мәселелер бар ма, соларды тиянақты түрде анықтау керек.
Есеп шығарудың жоспары дұрыс құрылғанда ғана есеп қатесіз шығарылады. Оқушыға есеп шығарудың негізгі кілтін ұсынатын идеяларға байланысты сұрақтар мен ақыл-кеңестер жүйелі түрде құрылғаны орынды:
а) осы сияқты есеп бұрын кездесті ма? Ол жағдай қалай еді, шығарылатын есепте қалай? Көбінесе берілген есепке ұқсас есеп беріле бермейді. Ол жағдай да:
ә) шығарылатын есепке ұқсастау, соған келетіндей есепті ойластыр.
б) берілген есепке мүлдем ұқсамайтын есеп келсе ше? Есептің шартындағы анықтамасын пайдалану, оның қасиеттерін еске алу.
в) Жоспар құру кезеңде Есептің берілгендерінің барлығы дерлік қолданылды ма? деген сұрақ жиі қойылып отырылуы тиіс.
г) Есеп шарты мен ізделіндісін түрлендіруге тырыс деген кеңес те көп пайдасын тигізеді.
Есеп шығаруға қойылатын негізгі талаптар: қатесіз шығару; негңздеу; толық шығару; мүмкіндігінше тиімді жолмен шығару, есепті қаттау.

Математиканы оқытудағы есептердің қызметтері.
Математика ғылым ретінде есептен пайда болған және есеппен дамиды. Мектеп математикасын есепсзі құру мүмкін емес. Математикалық есеп оқушылардың ұғымдарды, теорияны және математика әдістерін меңгерудің тиімді де, айырбасталмайтын құралы болып табылады. оқушылардың ойлау қабілеттерін дамытуда, оларды тәрбиелеуде, біліктері мен дағдыларының қалыптасуында, математиканың практикамен байланысын көрсетуде есептің алатын орны зор. Математиканы оқытудағы басты мақсаттарға жетуге есеп - басты қызметші болып табылады. Есептің негізгі міндеттері: оқыту, тәрбиелеу, дамыту, бақылау болып табылады. барлық есептер оқыту м.ндетін орындайды. Басқаша айтқанда, кез келген есепті шығарғанда оқушы математикалық білім алады, шығару біліктілігі қалыптасады, дағдыға ие болады, яғни математикалық білім деңгейі жоғарлайды.
Есеп оқушыларыдың логикалық ойлау, кеңістікті елесету, жеке бас қабілеттерін дамытуға бірден-бір себепші болатын басты құрал болып таблады. Оқушылардың білімін, біліктілігін және дағдысын анықтауды міндеттерді де көбінесе есепке жүктеледі.
Математиканы оқытудың міндеттері мен негізгі қағидалары.
Математиканы оқыту жөніндегі жалпы міндеттер:
1) Математиканы оқытудың ерекшеліктерін анықтау жəне оларды ғылыми негіздеу;
2) педагогикалық процестің жалпы заңдылықтарын математиканы оқытудың
нақты ерекшеліктеріне қолдану процестерін зерттеу;
3) математиканы оқытудағы озат тəжірибені зерттеу жəне қорытындылау;
4) педагогикалық жаңалықтар мен жетістіктерді математиканы оқыту процесіне икемдеу жəне практикаға енгізу техникасы мен əдістемесін жасау.
Сонымен, бұл міндеттерді шешу ғылыми негізделген, практикада сыннан өткен оқыту əдістемесі мен əдістерін мектеп өміріне енгізу болып табылады.
Математиканы оқыту жөніндегі жеке міндеттер:
1)оқытуды ұйымдастыру формаларын жасау;
2) оқушылардың білімін бағалау жəне оқытудын, жеке əдістері мен
тəсілдерін жасау;
3) оқыту процесінің тиімділігін тексеру;
4) мұғалімнің сабаққа дайындалуының мəнін ашып көрсету;
5) кластан тыс жұмыстарды жүргізу ерекшеліктері мен мазмұнын ашып көрсету.
Мектеп математика курсының мазмұны мен құрылымына арқау болатын қағидалар:
Мақсаттылық қағидасы. Уақыт талабына сай тиімді жүзеге асыруға болатын ұғымдар енгізілуі керек.
Дамыту қағидасы. Математика курсында қамтылған іргелі ұғымдарды енгізу және баяндаудың түрлі тәсілдері арасынан оқушылардың ойлау қабілетін дамытып, ғылыми-теориялық білімінің кеңеюіне жоғары деңгейде ықпал жасайтындарын қолдану қажет.
Проблемалық қағидасы. Курс мазмұнына енген әрбір ұғымды оқып-үйрену иерархияланған проблемалар жүйесін қою мен оны шешу жағдайында жүргізілуі тиіс.
Әдіснамалық қағидасы. Математикадағы ғылыми шығармашылықтың негізгі әдістері болып табылатын әдістерді қолдану керек және ол әдістер қолданып қана қоймай, ... жалғасы

Сіз бұл жұмысты біздің қосымшамыз арқылы толығымен тегін көре аласыз.