БІРТЕКТІ ЕМЕС ГАЛАКТИКАЛАР ҚҰРЫЛЫМЫН ЭНТРОПИЯЛЫҚ ТАЛДАУ

Пән: Автоматтандыру, Техника
Жұмыс түрі: Материал
Тегін: Антиплагиат
Көлемі: 7 бет
Таңдаулыға:

2. 1 Бейсызық жүйелердегі бифуркациялар

Бифуркация - бұл тәуелді параметрлердің өзгеруі кезіндегі динамикалық жүйе күйінің сандық өзгерісі, яғни жүйенің күйі сол жүйенің параметрлеріне тәуелді.

Бастапқыда мына өрнекпен бейнеленетін бейсызық математикалық маятниктің қарапайым динамикалық жүйесін қарастырайық:

. (2. 1)

(2. 1) теңдеуі бейсызық болып табылады, оның шешімі көптеген бейсызық теңдеулердің шешімі сияқты элементар функциялар арқылы бейнеленбейді, сондықтан оның сандық шешімін алу қажет. Ауытқудың жеткілікті аз бұрыштары кезінде ( 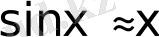, мұндағы х үшін маятниктің ауытқу бұрышы белгіленген), теңдеу сызықты 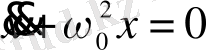болады, оның шешімі мына түрде жазылады:

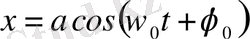
мұндағы 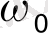- тербеліс жиілігі, а - амплитуда, 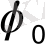- бастапқы фаза.

Маятник қозғалысының зерттеу нәтижелерін 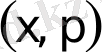жазығындағы қисықтар жиыны түрінде көрсеткен ыңғайлы, ондағы 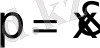- бұрыштың өзгеру жылдамдығы. 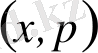жазығы жазық фазасы деп аталады. Қозғалыстың параметрлік заңдылықтарының 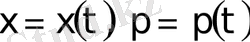түрінде анықталатын қисықтары - фазалық траекториялар (2. 1 сурет) .

Сызықты осциллятордың фазалық траекториялары энергияның сақталу заңымен берілетін эллипс болып табылады. Математикалық маятник үшін бұл ауытқудың аз бұрышы кезінде мүмкін болады. Ауытқу бұрыштарының үлкен мәндері кезінде математикалық маятниктің басқа жаққа айналуы мүмкін [7] .

(2. 1) теңдеуінің аналитикалық шешімі едәуір күрделірек, және біз маятниктің қозғалысын сандық зерттейтін боламыз. (2. 1) бірінші ретті теңдеулер жүйесі түрінде жазайық:

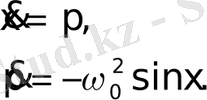(2. 2)

Мұнда 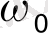жиілігі басқарушы параметр болып табылады. Жиілікті өзгерте отырып, жүйенің күйін өзгетуге болады.

2. 1 суретте көрініп тұрғандай берік және берік емес нүктелер болады, шеңбер центрі берік, ал ер-тоқым түріндегі нүктелер берік емес болып табылады.

2. 1 сурет - Бейсызық маятниктің фазалық портреті

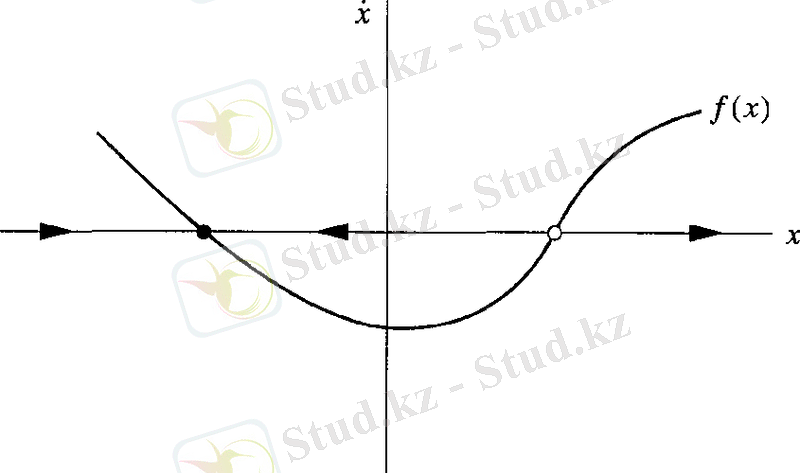
Берік және берік емес нүктелерге толығырақ тоқталайық. Тербеліс траекториялары берік нүктеге ұмтылып, ал берік емес нүктеден кететін болсын. Сонда фазалық портретті 2. 2 сурет түрінде көруге болады.

Қара нүкте бұл 2. 1 суреттегі шеңбер центріне сәйкес келетін берік нүкте, ал ақ нүкте ер-тоқым центріне сәйкес келеді. Берік нүкте математикалық маятниктің тыныштық күйіне сәйкес келеді, ал берік емес нүкте, математикалық маятниктің вертикал жағдайына сәйкес келеді, және аз тербелістер оны бұл күйден шығаруы мүмкін. Берік және берік емес нүктелер бифуркация теориясында маңызды әсерге ие. Қарапайым мысал ретінде бірінші ретті дифференциалды теңдеу үшін бифуркациялық режимдерді зерттейміз:

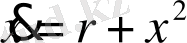. (2. 3)

(2. 3) теңдеуінің параметрлерін қарастырайық. Үш жағдай мүмкін.

r<0 кезінде векторлық өріс екі ерекше нүктеге ие болады, оны (2. 3) теңдеуінің оң жағын нөлге теңестіріп табуға болады, сонда 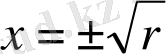. Олардың біреуі ( 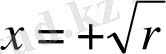) берік болады, басқасы ( 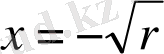) - берік емес.

r=0 кезінде векторлық өріс жалғыз жартылай берік гиперболалық емес ерекше 0 нүктеге ие болады.

r>0 кезінде векторлық өрістің ерекше нүктелері болмайды (2. 3 сурет) .

Бифуркацияның мұндай түрі негізгі ер-тоқым деп аталады.

Осылайша, негізгі ер-тоқымды бифуркация жартылай берік ерекше нүктенің пайда болу процесі, және бұдан кейінгі оның берік және берік емеске ыдырауы

2. 2 cурет - Фазалық жазықтағы берік және берік емес нүктелер

немесе керісінше - берік және берік емес ерекше нүктелердің жартылай берік нүктеге қосылып, кейін жоғалу процесі ретінде бейнеленуі мүмкін.

2. 3 cурет - (2. 3) теңдеуі бифуркациясының әртүрлі режимдері

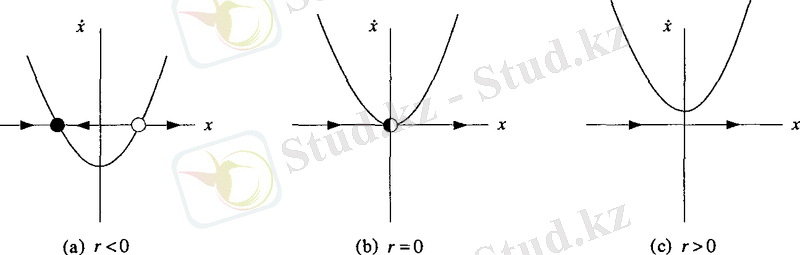
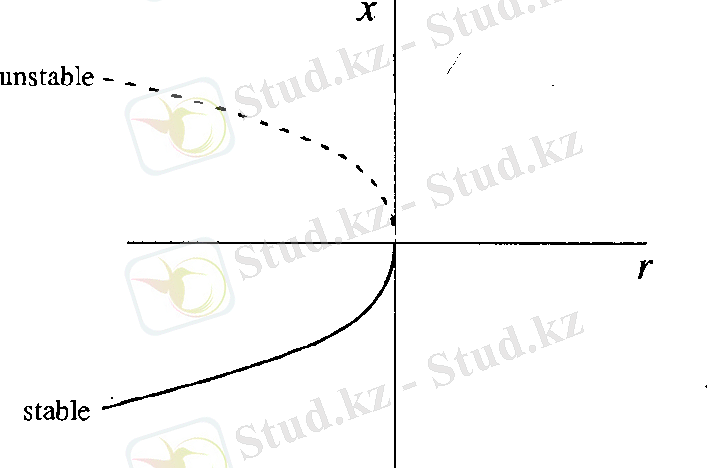
(2. 3) теңдеуінің бифуркациялық диаграммасы 2. 4 суретте көрсетілген. Үздік сызық берік емес, ал тұтас - берік нүктелерге сәйкес келеді. 2. 3 суреттен көрініп тұрғандай, r параметрінің өзгеруі кезінде жүйе күйін өзгертеді.

Сондай-ақ мына теңдеулер үшін бифуркациялық режимдерді қарастырайық:

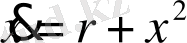. (2. 4)

(2. 4) теңдеуінің шешімі (2. 3) теңдеуінің шешіміне ұқсас, тек керісінше жаққа.

Екі тармаққа бөліну бифуркациясы деп аталатын тағы бір бифуркация түрі бар. Мұндай екіге бөліну симметриясы бар астрономиялық тапсырмаларда ортақ болып табылады.

Екі тармаққа бөліну бифуркациясы үшін теңдеу түрі:

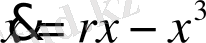(2. 5)

2. 4 cурет - (2. 3) теңдеуінің бифуркациялық диаграммасы

Егер мән берсек, онда бұл теңдеу х айнымалысының -х айнымалысына ауысуына қатысты инвариантты.

2. 5 суретте r әртүрлі мәндері кезіндегі векторлық өрістер көрсетілген.

2. 5 cурет - Екі тармаққа бөліну бифуркациясының бифуркациялық режимдері

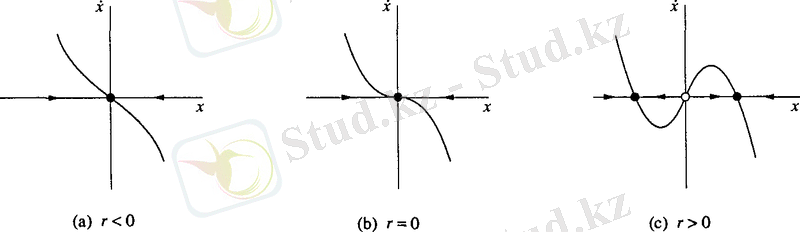
r<0 кезінде, жалғыз қозғалмайтын нүкте және ол тұрақты. r=0 кезінде қозғалмайтын нүкте бұрынғысынша тұрақты, бірақ айтарлықтай әлсіз, өйткені сызықтылық жоғалады. (2. 5) теңдеуінің шешімдері енді экспоненциалды емес, уақыт бойынша алгебралық функция әлдеқайда баяу құлайды. Ақырында, r> 0 кезде берік нүкте берік емес нүктеге айналады. Екі жаңа берік қозғалмайтын нүкте 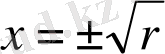симметриялы орналасқан берік емес нүктенің екі жағынан да пайда болады.

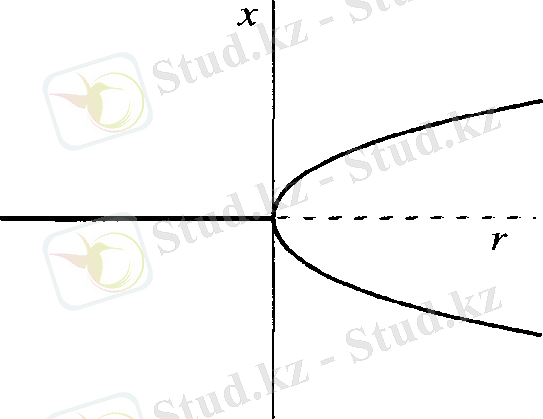
"Екі тармаққа бөліну" терминінің себебі, бифуркациялық диаграмма тұрғызғанда түсінікті болады (2. 6 сурет) .

Енді уақыты дискретті жаңа динамикалық жүйелер класын қарастырамыз. Бұл жүйелер, белгілі болғандай, әртүрлі аталады: теңдеу айырмасы ретінде, рекуррентті қатынастар, қайталама бейнелер, немесе жай ғана бейнелер.

2. 6 cурет - (2. 5) теңдеуінің бифуркациялық диаграммасы

Бейнелер табиғи құбылыстардың моделі ретінде әртүрлі туындайды. Кейбір ғылыми контексттерде бейнелер уақыттан дискретті түрінде қарастырылады. Сандық электроникада, астрономиялық мәліметтер бөлігінде, сондай-ақ кейбір жұлдыздар шоғырын қарастырған кезде осылай болады.

Бейнелеуді хаостың мысалдарының бірі ретінде қарастыруға болады. Көптеген астрономиялық құбылыстар хаостық тәртіпке ие. Шынында да, бейнелеулер бейсызық дифференциалдық теңдеулер тәртібіненде көп нәрсеге бейім, өйткені х секірулер нүктелері өз орбиталары бойынша дискретті (2. 7 сурет) .

2. 7 cурет - Қарапайым бейнелеудің секірулері

Бейнелеуді зерттеу әлі де бастапқы күйде тұр, бірақ айтарлықтай прогресс компьютерлердің дамуы арқасында соңғы жиырма жылда байқалды. Бейнелеуді уақыты дискретті болып табылатын сандық компьютерлерде анықтау оңай әрі тез. Мұндай компьютерлік зерттеулер күтпеген және әдемі модельдер қатарын анықтады, олар өз кезегінде, жаңа теориялық өңдеулерді шешуге мүмкіндік берді.

Негізінде хаосты периодты екі еселендіру арқылы моделдеу мына теңдеумен бейнеленетін логикалық бейнелеуде жасалады:

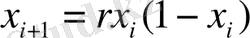, (2. 6)

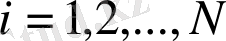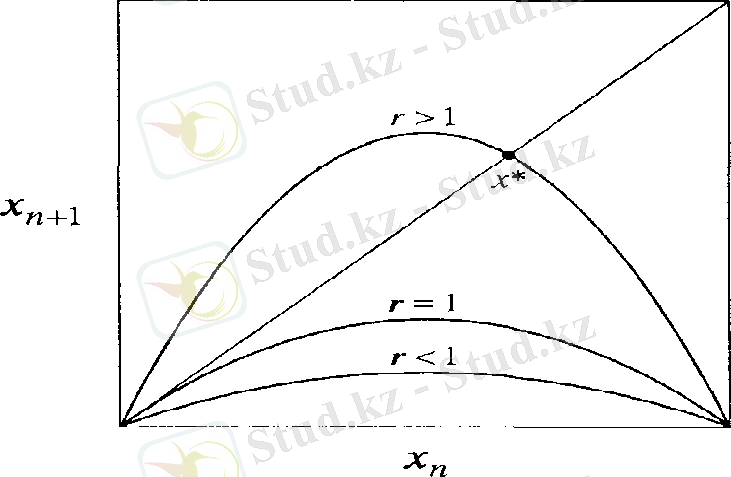
мұндағы , номеритерация. r >1 кезінде (2. 8 сурет) тепе-теңдіктің екі нүктесі болады. х _n ₊₁ = f ( x _n ) бейнелеудің беріктігін анықтау үшін тыныштық нүктесіндегі f '( x ) шамасын анықтаған жөн. Егер f '( x ) >1, тыныштық нүктесі берік емес. 1< r <3 кезінде логикалық теңдеу екі тыныштық нүктесіне ие болады: х= 0, ( r -1) / r ; сонымен қатар координата басы - берік емес нүкте, ал тыныштықтың екінші нүктесі берік.