Біртектілік дәрежесін ескерілген екі өлшемді объектілердің информациялық энтропиясы

Пән: Информатика, Программалау, Мәліметтер қоры
Жұмыс түрі: Материал
Тегін: Антиплагиат
Көлемі: 6 бет
Таңдаулыға:

Біртектілік дәрежесін ескерілген екі өлшемді энтропиясы

Ашық жүйелер энтропиясында өзұқсас және өзаффиндік режімдерін анықтаумен байланысты мәселелер маңызды болып табылады. Егер анықтаушы айнымалылардың саны бірліктен көп болса, ал осы айнымалылар бойынша ұқсас коэффиценттер түрліше болса, фракталдық объектіні өзаффиндік деп атайды. Егер фракталды объектілердің иерархиялық бөліктері барлық айнымалылар бойынша бірдей ұқсас коэффиценттерге ие болса, объектіні өзұқсас деп атайды. Осыдан бұрын З. Ж. Жаңабаев [8] өзаффинділік ( 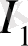) пен өзұқсастың ( 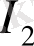) информация-энтропиялық критерийлерін информация мен энтропияны жүзеге асыру ықтималдығы тығыздығының жылжымайтын нүктелері түрінде анықтаған болатын:

, ; , . (2. 8)

Соңғы жылдары жаңа жалпылама статистикалық механика дамып келеді, оны Цаллис статистикасы деп немесе Гиббстың жалған канондық статистикасы деп атауға болады [8] . Осындай теориялардың негізін келесі түрдегі экспоненциалды функцияны пайдалану құрайды:

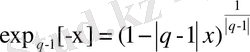, (2. 9)

Мұнда 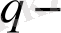біртектілік емес параметрі. шегінде біз кәдімгі экспонентті аламыз. Енгізу мағынасына қарай

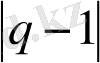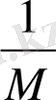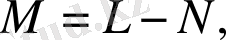
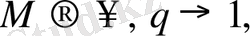~ , (2. 10)

мұнда, тұйық жүйелер бөлшектерінің саны, 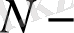жүйе тармағының бөлшектер саны. Гибстың канондық үлестіруіне сәйкес келетін тепе-тең күйдің толыққанды статистикасы 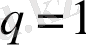жағдайында қол жеткізіледі. 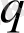параметрі бірлігінен айырмашылығы статистикалық тепе-теңдік дәрежесін, жүйенің біртектілігін сипаттайды.

Біртектілік дәрежесін ескере отырып, толық энтропияны 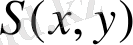анықтаймыз. Айнымалылар ретінде бір өлшемді және шартты ықтималдылықты 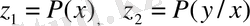қабылдаймыз. (2. 9) формулаға сәйкес мынаған ие боламыз:

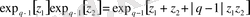(2. 11)

Сол жақ бөлігін туындыдан болған « 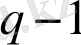логарифм» деп көрсетіп, мынаны аламыз:

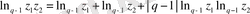. (2. 12)

(2. 12) формуласынан аддитивті емес « 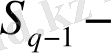энтропия» үшін келесі мән шығады:

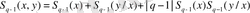. (2. 13)

шегінде біз аддитивті энтропияға ие боламыз .

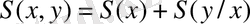(2. 10) формуласы бойынша 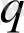анықтамасына сәйкес, оны эксперименттік деректерден анықтауға болады. Геометриялық объектілердің біртексіздігін сипаттау үшін, кіші параметрді енгіземіз:

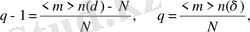(2. 14)

мұнда, 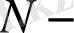нүктелердің (есептеудің) жалпы саны, 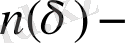ең болмағанда бір нүкте бар 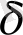өлшем масштабты ұяшықтар саны, 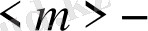ұяшықтағы нүктелердің орташа саны.

Оңайлау болу үшін, біз бұдан әрі 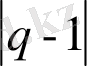орнына 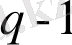мәнін пайдаланамыз, қажет болған жағдайда оң белгіні және ізделінуші физикалық шаманың нормалану шартын таңдаймыз.

(2. 9) мәнін пайдалана отырып, біз тең емес жүйенің күрделігінің, белгісіздігінің бірден-бір шамасы - информациялық энтропияның 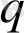-ге тәуелділігін анықтаймыз. 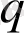параметрімен сипатталатын жалған тепе-тең үдеріс үшін, информацияны мына түрде анықтаймыз:

I = - ln _{q

-1} P (2. 15)

Осыдан келіп, ықтималдылықты информация функциясы деп аламыз:

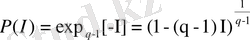. (2. 16)

Информацияны жүзеге асыру ықтималдығы үлестіруінің тығыздық функциясы 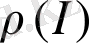былай анықталады:

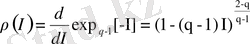. (2. 17)

Энтропия информацияның орташа мәні ретінде анықталады:

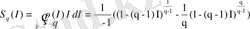. (2. 18)

Өзұқсас мәндерді 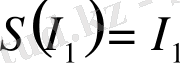и 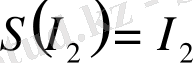көріністің жылжымайтын нүктелері ретінде табамыз

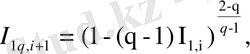(2. 19)

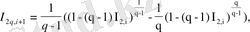(2. 20)

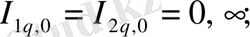
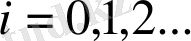Сөйтіп, 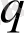мәні информация және информациялық энтропия мәндері арқылы өзұқсас және өзаффиндік күйінен жүйенің ауытқуын сипаттай алады. Мультифракталды талдауда кейбір 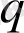параметрі 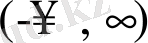аралығында беріледі, алайда оның физикалық мағынасы айқын емес күйінде қалып отыр. Алайда, біз келесі шартпен атап өтеміз:

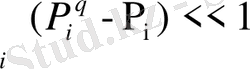, (2. 21)

(2. 9) формуласымен анықталатын Цаллис энтропиясы Реньи энтропиясымен сәйкес келеді:

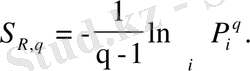(2. 22)

[9, 10] жұмыстарда жалпылама метрикалық сипаттама деп аталатын ретсіздіктің жаңа сипаттамасы енгізілді. Екі өлшемді объектінің жалпылама метрикалық сипаттамасы келесі формуламен анықталады:

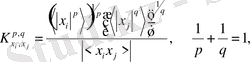(2. 23)

мұнда, 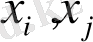- айнымалылар, 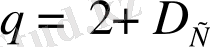, 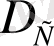- корреляциялық өлшемділік. Егер 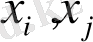ерікті айнымалылары болса, онда осы параметр жалпылама метрикалық сипаттамасы деп аталды (оны реттіліктің метрикалық параметрі деп атауға да болады) егер 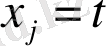- уақыт болса, онда - реттіліктің эволюциялық параметрі болады.

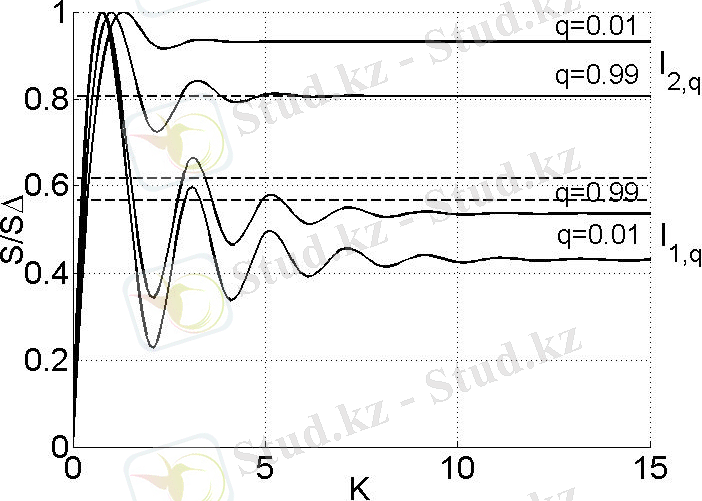
(2. 19), (2. 20), (2. 22) формулаларына сәйкес өзұқсас және өзаффиндік режімдеріне ашық жүйелер эволюциясының әмбебап энтропиялық заңдылықтары 2. 10 суретте берілген, мұнда 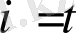деп қабылданған. Осы формулаларда энтропия бірлікке нормаланған. 2. 10 суретте көрсетілген диаграмма q біртектілік дәрежесінің өзгерісін ескереді.

2. 10 сурет - Информация - энтропиялық диаграмма. .

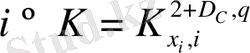$D:\Саят Ахтанов\Саят\НАУКА\Двумерная энтропия\Двумерная энтропия\SSmaxKpq.jpg$

2. 3 Зерттеу нәтижелері

Айнымалы жұлдыздарды энтропиялық талдау

Келесі объектілер зерттелінді: FU Ori, PV Tel, S Dor, UV Cer бақылау уақыты 1950 жылдан 2010 жылға дейін. Fu Ori және PV Tel аталған зерттелінуші объектілердің уақыттық қатарлары үшін, бифуркациялық диаграммасы салынып, сондай-ақ жалпылама метрикалық сипаттама 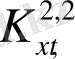берілді.

2. 11 сурет - FU Ori типті айнымалы жұлдыздың (a), PV Tel типті айнымалы жұлдыздың (b) бифуркациялық диаграммасы

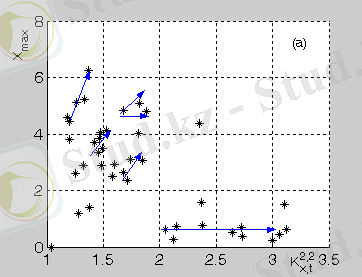
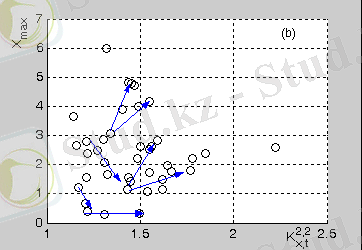
2. 11 (a), (b) суретінде FU Ori типті мен PV Tel айнымалы жұлдыздардың бифуркациялық диаграммасы сигналдың уақыт қатарының максималды мәні X _max мен жалпыланған метрикалық сипаттаманың K _pq тәуелділігі ретінде алынды. Суреттен тәуелді параметрлердің өзгеруі кезінде екіге бөліну симметриясы көрінеді.

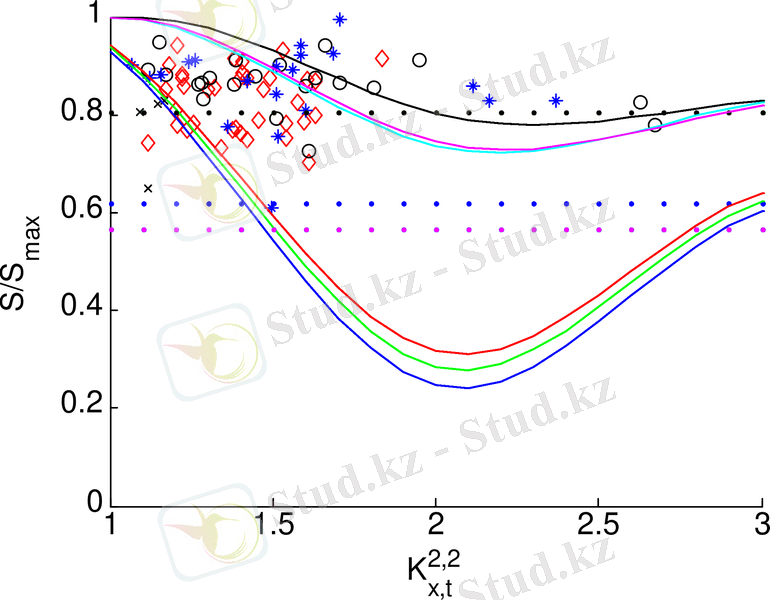
Айнымалы жұлдыздардың бифуркациялық диаграммасын - сапалық өзгерісті Шеннон энтропиясы арқылы көрсетуге болады. FU Ori, PV Tel, S Dor, UV Cer айнымалы жұлдыздары үшін бір өлшемді энтропияның (Шеннон) реттіліктің метрикалық параметріне тәуелділігі алынды.

2. 12 сурет - Бір өлшемді энтропияның (Шеннон) реттіліктің метрикалық параметріне тәуелділігі