Ғаламдардың айналмалы қозғалысы

Пән: Астрономия
Жұмыс түрі: Материал
Тегін: Антиплагиат
Көлемі: 3 бет
Таңдаулыға:

Ары қарай зерттелетін ғалам түрінде эллиптикалық ғаламдарды таңдаймыз. Бұл тек ғана қойылған міндеттердің аналитикалық шешімін жеңілдетіп ғана қоймайды, сонымен бірге оны нақты бақылау мәліметтерімен салыстыруға мүмкіндік береді. Бұндай Е-ғаламдар, дұрысында, кіші жұлдыз құраушылардан тұрады, яғни, өзімен бірге жұлдыз «газ» ұсынады, және дұрыс формалы болып келеді - сығудың әртүрлі дәрежелерімен эллипсоидтар.

Ары қарай айналу эллипсоиды формасымен эллиптикалық ғаламдарды қарастырамыз, екі басты осі бір-біріне тең, яғни инерцияның жекелеген сәттері мынандый: 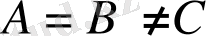. Сонда, сәйкесінше [15], потенциал 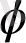, бұрышқа байланысты болмайды, ерікті болуы мүмкін саламыз 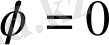. сонда, осы жағдай үшін бағытталған косинустар үшін есептей отырып жалпы өрнекке сәйкес (6) және оларды қойып (12), вакуум потенциалын табамыз

. (13)

Ғаламның таңдалған формасы үшін айналмалы қозғалыстың оның теңдеуі мынандай

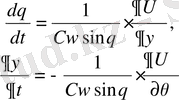. (14)

Осы жүйенің теңдеуі жөнінде екі түсініктеме жасаймыз. Біріншіден, 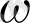шамасы айналмалы қозғалыстың алғашқы интегралын ұсынады, яғни 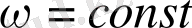. Инерцияның меншікті сәтіне салыстырмалы бұрыш жылдамдығының компонентін сипаттайды . Екіншіден, шешім кезінде (14) айнамалы ғаламның бұрыштық жылдамдықтары кішкентай екені анықталды. Бұл бұрыш жылдамдығы және бұрыш үдеткіші квадраттарымен елемеуге мүмкіндік берді. Және, соңында осы жерде қоямыз .

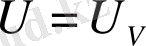Енді, (13) сүйене отырып, бұрыштар бойынша оның туындыларын есептейміз 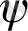және 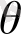, сондан кейін оларды жүйеге қоямыз (14) . Ғалам айналуының бұрыш жылдамдығы кіші түрінде, бұрыштардың өзін кіші деп есептеуге болады. Оларды квадраттармен елемей, сонымен бірге интервалдардың кез келгенінің шамасын ескере отырып (13) 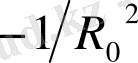көп емес, айтарлықтай дәлдікпен аламыз

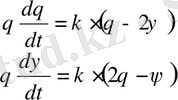, (15)

бұнда коэффициент 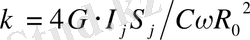. Теңдеу жүйесінің алғашқы тәртіптің дифференциалды теңдеуіне жеңіл айналдыруға болады

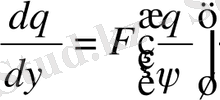, (16)

Оң жақтағы бөлім .

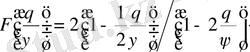Теңдеудің шешімі (16) стандартты квадратурамен сипатталады

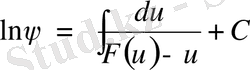соған қарамастан бұнд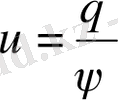а , а 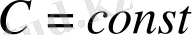. Квадратура екі қосындыдан тұрады, оның біреуі пропорционалды 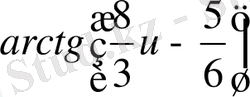, жоғарыдан шектеулі, соған орай, даму сипатының шешімдеріне алып келе алмайды. Екінші қосында 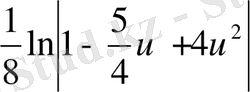, керісінше, бұндай мүмкіндікті ұсынады. Сөйтіп, 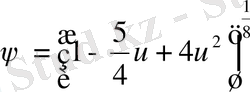. Ары қарай байқайтынымыз, бұрыштар шамасы жіберілген кішілігі күшінд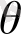е және 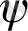, олардық қатынасы бірліктер қатарына ие, яғни. 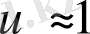. Сондықтан екінші теңдеуден (15) жақындасқын қатынасты аңғарамыз 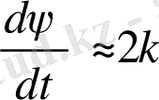. Сөйтіп, ізделетін шешім даму бүрышы үшін мынандай түрде

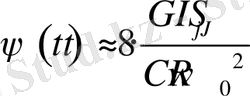. (17)

Алынған нәтижеге сүйене отырып осі бойында эллиптикалық ғаламның айналу бұрышы жылдамдығын жеңіл есептеуге болады. Шын мәнінде, осы жағдайда былай болғандықтан , онда оның үлгісі тең

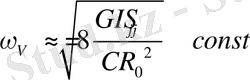. (18)

Бұл өрнек эллиптикалық ғаламның вакумм әсері арқасында ие болып отырған айналудың бұрыштық жылдамдығын сипаттайды.

Ғалам айналысының қоздырылған жылдамдығының бағасы

Алып эллиптикалық ғаламды қарастырамыз NGC 4486 (М 87), қашықтығы дейін 15 Мпк тең болатын, ал өзіндік көлемі 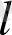тең келетін 60 Кпк. (Байқаймыз 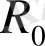ретінде таңдауға болады және жұп немесе топтар массасы орталығынан ғаламға дейінгі ол өзі кіретін) Жоғарыда келтірілген вакуум тығыздығының мәндері есебінен өрнектің шамасын бағалаймыз (18) .

Қабылдай отырып 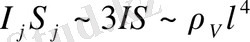және инерцияның меншікті сәті , 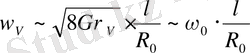табамыз. Бұл жерге қажетті шаманы жеткізе отырып келесі бағаны аламыз .

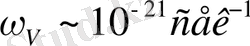Егер барлық ғаламдар массасы орталығымен байланысты есептеудің жүйесін таңдайтын болсақ және оның құрылымын есепке алатын болсақ, онда нәтиже басқандай болады. Шындығынды, элиптикалық ғаламдардың ең ірісі, белгілі болғандай, жекелеген топтардан ерекшеленеді cD-ғаламдар. Оларда шағын жұлдыз жүйелері және жұлдыздардан алып бөлінген қабаттары бар. Қабаттар көлемі ондаған және жүздеген килопарсекке жетеді. Сонымен, осы жүйе үшін де М 87 оның орталық компоннеттінің радиусы 8 Кпк шамасында құрайды, ал қабат орталықтан 60 Кпк дейін бақыланады. Сондықтан, жобалай отырып 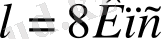, ал 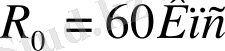, келесі бағаны аламыз .

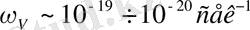Осыдан алынатын маңызды шешім - ғалам бізден алыс тұрған сайын, олардың бұрыштық жылдамдығы аз болатындықтан 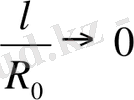. Кез келген жағдайда, вакуумның антигравитациялық әсерімен келісілген бұрыштық жылдамдықтың сол бөлімімен. Физикалық көзқарас бойынша бұл жағдай ньютон механикасында болмайтын қоздырылған қозғалыс үшін нүктелік денеге өтуін білдіреді.

Сонымен, антитартылыстың вакуумдық күшімен келісілген нақты эллиптикалық ғаламдар бұрыш жылдамдығының бағасы, шамасын құрайды 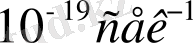. Сонымен бірге, бақылау мәліметтері айтарлықтай үлкен шаманы береді.

Сөйтіп, эллиптикалық ғаламдар үшін NGC 1600, сәйкес [16], айналудың бұрыш жылдамдығы 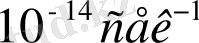шамасын құрайды. Осындай тәртіп бойынша бұрыш жылдамдықтарының мәні басқа да Е-ғаламдарда да бар [17] . Алшақтау себебі, осындай ғаламдар өзінің даму процесі кезінде гравитациялық өтулер әртүрлі механизмдері арқасында сәйкесінше айналу сәтін таңдағандығымен қорытындылады (мысалы, [18, 19] жұмыстарын қара) . (18) өрнекке сәйкес, вакууммен келісілген ғаламның алғашқы немесе түрткі бұрыш жылдамдығын көруге болады.