Вакуумдық антигравитация әсеріндегі ғаламдардың айналмалы қозғалысы: потенциалдық есептеулер және әлемнің ғаламдық айналу параметрлері


1 Ғарыштық ваккум
Әлемнің жаһандық қасиеті ғарышнама үшін әрқашан маңызды ретінде қарастырылады. Соған қарамастан олардың түсінігі көп жерлерде құрамын анықтайтын нысандардың параметрлерімен анықталады, олар ең алдымен, - ғаламдар және оның кластерлерінің динамикалық сипаттамалары. Көптеген жұмыстарда, мысалы [1- 13], ғаламдар динамикалары ілгерілемелі қозғалыс теңдеуі негізінде қарастырылады. Ғаламдарды нүктелік дене түрінде ұсыну бойынша соңғы шарт пара-пар. Ғалам кластерінің дәл осындай үлгісі (ғаламда нүктелік жұлдыздар жүйесі сияқты) қазіргі ғарышнамада кеңінен пайдаланылатын N-body simulation әдісінің негізін құрайды.
Солардың арасында, аз өзара қашықтықта орналасқан маңызды астрономиялық нысандар қатары үшін, - қос ғаламдар, ғаламның тар топтары, өзара әрекет ететін және ағатын ғаламдар -
 бұндай жақындасу әдейі жарамсыз болып табылады. Көрсетілген жүйелердің дамуын зерттеу үшін ғаламдардың өздерінің көлемдерінің есебі және ілгерілемелі-айналатын қозғалыстың теңдеуін қолдану талап етіледі.
бұндай жақындасу әдейі жарамсыз болып табылады. Көрсетілген жүйелердің дамуын зерттеу үшін ғаламдардың өздерінің көлемдерінің есебі және ілгерілемелі-айналатын қозғалыстың теңдеуін қолдану талап етіледі.
Сонымен бірге, астрономиялық нысандар үшін ғарышнама ауқымында антигравитациялық тебіліс күшінің есебі қажетті болғандықтан тек бір ғана гравитациялық өзара әрекет олардың динамикасының толық сипаттамасын бере алмайды. [14] .
Шындығында, бүгінде Әлем динамикасымен негізінен вакууммен біріктірілген антигравитацияның өзі басқаратыны нақты белгіленген. Соған қарамастан Әлем жылдамдықпен кеңеюде, бірақ кеңістік-уақыттың өзі статистикалық болып қалып отыр. Сонымен бірге, кеңеюге қарамастан ғарыш вакуумының тығыздығы тұрақты шамасы болып табылады. Сындық тығыздық бірлігінде (
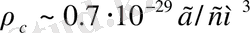 ) ол
) ол
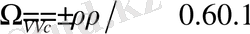 сияқты бағаланады. Сондықтан еселі нысандар динамикасын тербелістік вакуумдық күшімен толықтырылған ілгерілемелі-айналмалы қозғалыстың теңдеуі негізінде меңгеру керек.
сияқты бағаланады. Сондықтан еселі нысандар динамикасын тербелістік вакуумдық күшімен толықтырылған ілгерілемелі-айналмалы қозғалыстың теңдеуі негізінде меңгеру керек.
Еселі ғаламдар қатарларының қозғалысын шектелген мәселе қойылуы шеңберінде де меңгеруге болады. Жалғыз және қос ғаламдар арасында шегара көбінесе айтарлықтай шартты болғандықтан, соңғы массалы екі астрономиялық дене міндеттерінің саналы жақындасуында оның инерция орталығының белгілі қозғалысымен бір дене есебіне келтіруге болады. Сонда осы нысанның ілгерілемелі-айналатын қозғалыстың теңдеуі жүйесі ілгерілемелі және айналмалы екі тәуелсіз бөлікке бөлініп кетеді.
Осы жұмыста антигравитацияның вакуумдық күшімен келісілген ғаламдардың айналмалы қозғалысының талдауы жүргізіледі. Оның негізінде Әлемнің жедел кеңеюінің параметрінің кеңістіктік анизотропиясы айналу осі айналуы, бар болуы және бағыты сонымен қатар, ғарыш вакуумымен мағыналанған барлық Әлемнің жахандық сипаттамалары зерттеледі. Ғарыш вакуумының канондық мәселесіне келетін болсақ - Әлемнің кеңеюі және оның жеделдетілген кеңеюі, солардың барлығы толығымен мақалада келтірілген [14] .
Келесі жұмыстың құрылымы.
Кіріспеде антигравитацияның вакуумдық күшімен келісілген ғаламдардың айналмалы қозғалысын зерттеу қажеттілігінің негіздемесі берілген. Екінші бөлімде ғаламдардың айналмалы қозғалысы теңдеуін шығаруға мүмкіндік беретін вакуумдық гравитациялық потенциал есептелді. Үшінші бөлімде айналмалы қозғалыстың алынған теңдеулерінің талдауы жүргізілді және айналымның сәйкес бұрыштары саналды (Эйлер бұрыштары) . Төртінші бөлімде антитартылыс вакуумдық күшімен келісілген, нақты эллиптикалық ғаламдар үшін бұрыштық жылдамдықтың бағасы берілді. Бесінші бөлімде
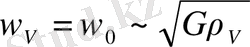 түрінде Әлем айналуының вакуумдық бұрыштық жылдамдығы өрнегі табылды. Бесінші бөлім Әлемнің айналу осінің ғаламдық кардинаттарын есептеуге және оларды ертеректе алынған бақылау мәліметтерімен салыстыруға арналған. Мақаланың ең соңғы жетінші бөлімде кеңістіктік бағытынан ғарышнама (вакуумдық) жеделдету параметлері тәуелділігі негізінде жұлдызды аспан солтүстік және оңтүстік жартышары үшін Хаббл диаграммаларының асимметриясының түсініктемелері берілді. Қорытындыда осы зерттеудің қорытындысы қысқаша келтірілген.
түрінде Әлем айналуының вакуумдық бұрыштық жылдамдығы өрнегі табылды. Бесінші бөлім Әлемнің айналу осінің ғаламдық кардинаттарын есептеуге және оларды ертеректе алынған бақылау мәліметтерімен салыстыруға арналған. Мақаланың ең соңғы жетінші бөлімде кеңістіктік бағытынан ғарышнама (вакуумдық) жеделдету параметлері тәуелділігі негізінде жұлдызды аспан солтүстік және оңтүстік жартышары үшін Хаббл диаграммаларының асимметриясының түсініктемелері берілді. Қорытындыда осы зерттеудің қорытындысы қысқаша келтірілген.
2. Вакуум күші және оның потенциалы.
Үлгі ретінде ғаламның қатты денесін таңдаймыз және антигравитация вакуум күшінің әсерімен массаның өздік орталығынан салыстырмалы оның айналуын қарастырамыз.
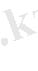
Бұл үшін координаттың үш үшбұрышты (вакуумного) жүйесін енгіземіз:
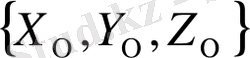 , кеңістіктік кейбір нүктелерімен байланысты
, кеңістіктік кейбір нүктелерімен байланысты
 ; салыстырмалы қозғалмаытын жүйені
; салыстырмалы қозғалмаытын жүйені
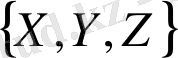 , ғаламаның инерция орталығымен байланысты
, ғаламаның инерция орталығымен байланысты
 ; және координаттың қозғалатын жүйесін
; және координаттың қозғалатын жүйесін
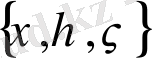 осы нүктеде орталықпен
осы нүктеде орталықпен
 .
.
Енді стандартты түрде Эйлер үш бұрышын береміз: упрецессия бұрышы
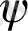 , қиылыс сызығымен құрылған
, қиылыс сызығымен құрылған
 жазықтық
жазықтық
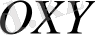 және
және
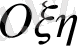 осінің бағыттарымен
осінің бағыттарымен
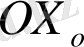 ; өзіндік айналу бұрышы
; өзіндік айналу бұрышы
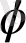 , сызығымен құрылған
, сызығымен құрылған
 және осі
және осі
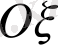 ; нутация бұрышы
; нутация бұрышы
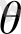 , осермен құрылған
, осермен құрылған
 және
және
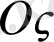 .
.
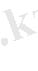
Және, ең соғында, ғалам ішінен
 ерікті нүктесін таңдаймыз, сөйтіп, координаттың абсолютті жүйесі орталығынан
ерікті нүктесін таңдаймыз, сөйтіп, координаттың абсолютті жүйесі орталығынан
 оған дейінгі қашықтығы
оған дейінгі қашықтығы
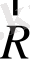 болуы, ал, ғаламлар инерциясы орталығынан
болуы, ал, ғаламлар инерциясы орталығынан
 оған дейінгі қашықтығы
оған дейінгі қашықтығы
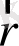 болуы үшін. Нүктелер арасындағы осы қашықтыққа сәйкес
болуы үшін. Нүктелер арасындағы осы қашықтыққа сәйкес
 және
және
 белгілейміз
белгілейміз
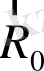 .
.
 нүктесі маңында
нүктесі маңында
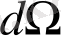 үш өлшемді көлемде жұмылдырылған
үш өлшемді көлемде жұмылдырылған
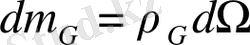 ғаламнан шексіз аз массаны аламыз.
ғаламнан шексіз аз массаны аламыз.
Ол абсолютті жүйесі орталығына

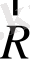 қашықтығында болса, оның орталығында орналасқан бірлік массасымен оның гравитациялық өзара әрекетінің күші
қашықтығында болса, оның орталығында орналасқан бірлік массасымен оның гравитациялық өзара әрекетінің күші
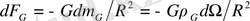 тең болады.
тең болады.
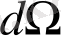 сол көлемде вакуум массасымен келісілген (гравитациялық тебіліс күші) гравитациялық антитартылысқа келетін болсақ, вакуум жағдайы теңдеуі есебінен
сол көлемде вакуум массасымен келісілген (гравитациялық тебіліс күші) гравитациялық антитартылысқа келетін болсақ, вакуум жағдайы теңдеуі есебінен
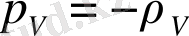
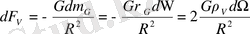 .
.
 (1)
(1)
ол тең болады.
Негіздеме кезінде (1) Фридмен үлгісіне сәйкес тартылыс жазықтық жинақтамасын құрады
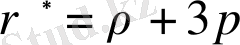 , бұл жерде
, бұл жерде
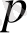 орта қысымы сол жағдай назарға алынды.
орта қысымы сол жағдай назарға алынды.
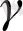 - векторлар арасындағы бұрыш болса
- векторлар арасындағы бұрыш болса
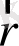 және
және
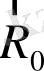 . Онда
. Онда
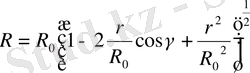 . (2)
. (2)
Жобаланған орындалған жағдаймен
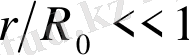 , аз парамертлер бойынша бірінші қатарлы мүшелерге дейін дәлдікпен гравитациялық тебіліс күші элементңн табамыз
, аз парамертлер бойынша бірінші қатарлы мүшелерге дейін дәлдікпен гравитациялық тебіліс күші элементңн табамыз
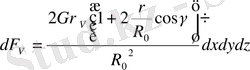 . (3)
. (3)
- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz