Гравитациялық жүйелерді өрнектейтін теңдеулер

Пән: Физика
Жұмыс түрі: Материал
Тегін: Антиплагиат
Көлемі: 6 бет
Таңдаулыға:

Гравитациялық жүйелерді өрнектейтін теңдеулер

Дербес (жергілікті) және толық (материялық) туындылар

Кейбір ортаның қозғалысын қарастырғанда екі тәсілді қолдануға болады: 1) сұйықтық күйін сипаттайтын шамалардың (мысалы жылдамдықтың, температураның, тығыздықтың, т. с. с. ) кеңістіктің берілген (координаттары бекітілген) нүктедегі өзгеруін қарастыруға болады (осы жағдайда сұйықтық сипаттамалары қозғалмайтындай етіп бекітілген құралмен өлшенеді) (бұл тәсіл Эйлер тәсілі деп аталады) ; 2) сұйықтықтың әр бөлшегінің (немесе сұйықтық элементінің (сұйықтықтың қалап алынған бөлшектерінің (бұл бөлшектер ұқсас қозғалу тиіс) айтарлықтай санын кіргізетін көлемшесінің) ) қозғалысын бақылауға, яғни координаттары уақытта өзгеретін әр бөлшекті сипаттайтын параметрлердің өзгерісін қарастыруға болады (сипаттамалар ағынмен бірге қозғалатын құрал көмегімен өлшенеді) (Лагранж тәсілі) .

Кейбір φ(M, t) шаманың берілген М нүктедегі уақыт ағысымен өзгерісін дербес (немесе локальды, жергілікті) деп аталатын туындымен сипаттайды:

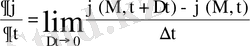(1)

Оны есептеген кезде М нүкте бекітілген (қозғалмайды) деп қарастырылады.

Берілген бөлшек (элемент) үшін φ(M, t) шаманың уақыттағы өзгерісі толық (немесе материялық) деп аталатын туындымен сипатталады, оны былай анықтайды. М деп берілген нүктенің t уақыт мезетіндегі орналасуын, ал М’ деп сол бөлшектің t+∆ t уақыт мезетіндегі орналасуын белгілейік. φ-ң уақыт бойынша толық туындысы деп

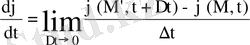(2)

шама аталады. Толық пен жергілікті туындылар арасындағы байланысты табу үшін, материялық туындыны есептегенде, М нүктенің x, y, z координаттары уақыттын функциялары, ал олардың уақыт бойынша туындылары ағынның М нүктедегі жылдамдығының құраушылары болып табылатынын еске алуымыз керек. Сондықтан, φ=φ(x, y, z, t) -ді t-ң күрделі функциясы ретінде дифференциалдап, мынаны аламыз:

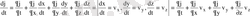, (3)

яғни

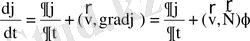, (4)

мұнда 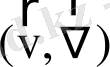деп 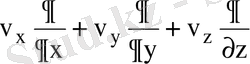оператор, яғни 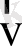жылдамдық пен символдық векторының «скалярлық көбейтіндісі» белгіленген.

Яғни қозғалыстағы элемент үшін φ мәнінің уақыттағы толық өзгерісі φ кеңістіктің әр (бекітілген) нүктесінде уақытта өзгертінімен, оған қоса кеңістікте де өзгеретінімен (бұл өзгерістерді элемент қозғалып, кеңістіктің бір нүктесінен басқа нүктесіне өткенде φ-ң уақыттағы өзгерісі ретінде сезеді) себептеледі. φ-ң кеңістіктегі өзгеруінің уақыт бойынша толық туындыға үлесі бұл шама кеңістікте қаншалықты тез өзгеретініне (grad φ) және бөлшек бір нүктеден басқа нүктеге қаншалықты тез өтетініне ( v ) байланысты болады.

Көрсетілгенге ұқсас векторлық А (M, t) шама үшін де дербес және толық туындылар ұғымын енгізуге болады:

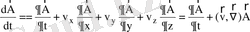(5)

Больцман теңдеуі. Вириал теоремасы

Алтыөлшемді фазалық кеңістіктің, яғни координаттар мен жылдамдықтардың алтыөлшемді кеңістігінің ұғымын енгізейік. Бөлшектің қозғалыс күйіне (яғни оның берілген уақыт мезетіндегі координттары мен жылдамдығына) фазалық кеңістіктегі бір нүкте сәйкес келеді, оның орналасуы 6 координат арқылы анықталады: үш әдеттегі кеңістіктік координат пен жылдамдықтың (немесе импульстің) үш құраушысы болып табылатын үш жылдамдықтық координат арқылы. Мұндай кеңістікті екіөлшемді фазалық жызықтықтың жалпылануы ретінде қарастыруға болады, бөлшектің бұл жазықтықтағы координаттары бөлшекті сипаттайтын кейбір шаманың мәндері мен оның бірінші туындысы (мысалы, бірөлшемді қозғалыс үшін олар - бөлшектің х координатасы мен жылдамдығы) болып табылады. Гармониялық осциллятор үшін мұндай жазықтықта оның тербелістерінің (қозғалысының периодты тізбегінің) кезеңін (фазасын) көруге болады, фазалық кеңістіктің мұндай аталуы бұған байланысты болса керек.

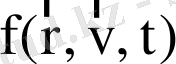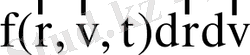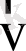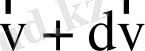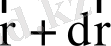Больцман теңдеуі - фазалық кеңістіктегі үлестірілу функциясы үшін теңдеу. көбейтінді жылдамдықтары -ден -ге дейінгі аралықта жатқан -ден -ге дейінгі көлемдегі бөлшектер санын, яғни фазалық кеңістіктің , 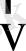нүктесі маңайындағы 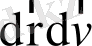фазалық көлеміндегі бөлшектердің санын береді, ал 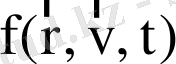функцияның өзі бөлшектердің сол нүктедегі фазалық концентрациясын береді.

Енді фазалық кеңістікте кішігірім 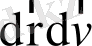көлем элементін таңдап алайық. Бұл элемент бөлшектердің (галактикалардың немесе жұлдыздардың) арақашықтығымен салыстырғанда көп, ал Әлем (немесе галактика) өлшемімен салыстырғанда аз болсын. Әр t уақыт мезетінде ол 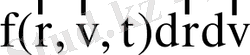бөлшекті кіргізеді. Фазалық кеңістіктегі үлестірілу функцияның уақыт бойынша толық туындысы

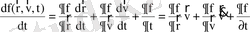. (6)

Мұнда бірінші мүше бөлшектердің 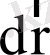көлемінен шығып кетуімен (және басқа, бұрында бұл көлемде болмаған бөлшектердің сол көлемге кіруімен), екінші мүше бөлшектер жылдамдықтарының 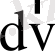аралығынан шығып кетуімен (және басқа, бұрында жылдамдықтары бұл аралықта жатпаған бөлшектердің сол аралыққа кіруімен), ал үшінші мүше концентрацияның берілген нүктедегі өзгеруімен байланысты деп түсіндіруге болады. Бұл жерде 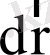көлем енді бекітілген нүкте маңайында емес, таңдап алынған көлем элементімен бірге жылжийтін нүкте маңайында алынатынын айту керек. Толық туынды есептелгенде, қалап алынған фазалық көлем элементіне t уақыт мезетінде кірген бөлшектер қозғалысы қарастырылады ғой (санақ жүйесі бөлшектермен бірге (олардың масса центрінің жылдмадығымен???) қозғалады) . Сонда, бұл бөлшектер қозғалғанда, олардың координаттары мен жылдамдықтары өзгереді, демек олар толтыратын фазалық көлем де өзгереді (ол созылу немесе сығылу мүмкін, оның пішіні өзгереді) және басқа 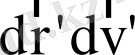көлем элементіне айналады. Егер бөлшектер бір көлем элементінен басқа көлем элементіне секірмелі түрде емес, біртіндеп өтсе (былайша айтсақ, біз қарастырып отырған көлемшедегі бөлшектердің саны соқтығулар, үлкен бұрышқа шашыраулар, т. с. с-мен байланысты кенет өзгермесе (бұл құбылыстар нәтижесінде бөлшектер біздің көлемшеге кенет енуі, немесе одан кенет шығып кетуі мүмкін) ), онда 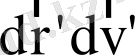көлем элементіндегі бөлшектердің саны көлемшедегі бөлшектердің санына тең болып қалады (жаңа бөлшектер біздің бөлшектер арасына кішкене уақыт ішінде терең кіріп үлгірмейді, сондықтан 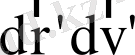көлемді алған кезде біз оларды айналып өте аламыз) : 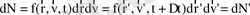(7) . Сөйтіп, қалап алынған фазалық көлем элементін координаттары бір біріне жақын және уақытта ұқсас өзгеретін бөлшектер алатын (бөлшектермен толтырылған) фазалық кеңістік (көлемінің) бөлігі ретінде қарастыруға болады.

Бұл көлемдегі бөлшектердің саны өзгермесе де, үлестірілу функцияның мәні өзгереді, өйткені оның мәні бөлшектердің берілген (масса центрлер болып табылатын???) нүктедегі концентрациясын береді, сонда, егер біздің көлемшеміз созылса, онда концентрация (демек үлестірілу функциясының мәні де) азаяды, және керісінше (былайша түсіндірсек, үлестірілу функцияның әр түрлі уақыт мезеттеріндегі мәндерін есептеген кезде, біз мәндері бойынша бірдей көлемдердегі ( ) (фазалық кеңістіктің ұяшықтарындағы) бөлшектер санын есептейміз, сонда біздің көлемшеміз созылса, мәні бойынша өзгермеген көлемдегі бөлшектердің саны азаяды; былай да айтуға болады: үлестірілу функция мәнін табу үшін, бөлшектердің саның олар алатын көлемге бөлу керек, сонда, егер бұл көлем созылса, өзгермеген бөлшектер саны артқан көлемге бөлінеді де, үлестірілу функцияның мәні азайған болып шығады) . Сонда (6) формуладағы бірінші мен екінші мүшелер қарастырылып отырған бөлшектер координаттарының бастапқы 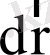аралығы мен жылдамдықтарының бастапқы 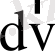аралығының созылуымен немесе сығылуымен байланысты болады.

Гамильтонның классикалық аналитикалық механикасының іргелі тұрғыларының біреуі - фазалық көлемнің сақталуы туралы заң (Лиувилль теоремасы) . Біздің белгілеулерде математикалық түрде бұны былай жазамыз: 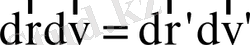. Бұдан бөлшектердің толық саны өзгермеген жағдайда мәні бойынша тұрақты фазалық көлем элементіндегі бөлшектер саны да өзгермейтіні шығады(жоғарыдағы 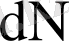үшін формуладан 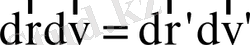жағдайда 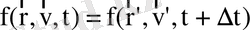болатыны, яғни үлестірілу функцияның мәні фазалық кеңістіктегі траектория бойымен тұрақты болып қалатыны көрінеді) . Сөйтіп, үлестірілу функциясының фазалық траектория бойымен алынған толық туындысы нөлге тең болады:

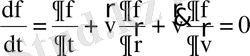. (8)

Бұл теңдеу Больцман теңдеуі деп аталады. Оны мынадай түрде де жазуға болады:

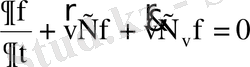, (9)

мұнда белгімен жылдамдықтар кеңістігіндегі набла операторы белгіленген:

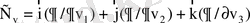
Больцман теңдеуін физикалық принциптерге сүйеніп те шығаруға болады. Егер бөлшектер көлемнің бір элементінен басқасына секірмелі емес, біртіндеп өтсе, онда үлестірілу функция үздіксіздік теңдеуіне қанағаттандыру тиіс:

. (*)

Бұл теңдеу координаттары бекітілген ( , 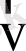) нүкте маңайындағы көлеміндегі бөлшектер саны тек олардың бұл көлем шекаралары арқылы келуі мен кетуіне байланысты болатынын көрсетеді. Ол көздер мен науалар жоқ болғандағы сығылатын сұйықтық қозғалысын өрнектейтін үздіксіздік теңдеуіне ұқсас: 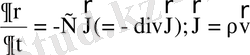, мұндағы - сұйықтық ағының тығыздығы; бұл теңдеу көздер мен науалар жоқ болған жағдайда кез-келген көлем элементіндегі тығыздық тек сол көлемді шектейтін бет арқылы өтетін сұйықтық ағыны нолге тең болмауына байланысты (яғни бұл көлемге бірдей уақыт аралығында ағып кіретін және ағылып шығатын сұйықтықтың мөлшері (массасы) бірдей болмағанда) өзгеретінін көрсетеді. Сұйықтық тығыздығы орнына бөлшектердің үлестірілу функциясын (яғни фазалық кеңістіктегі концентрациясын) қойып, және әдеттегі үшөлшемді (координаталық) кеңістіктегі ағынына қоса жылдамдықтар кеңістігіндегі ағынды еске алып: 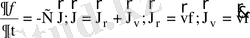, (*) теңдеуді аламыз. Ал одан мен 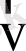тәуелсіз шамалар болып қарастырылатынын және үдеу жылдамдыққа тәуелсіз екендігін естерімізге түсіріп, (9) теңдеуді аламыз.

Ол (орташа) гравитациялық өріс баяу өзгеретін жағдайда жарамды (егер олай болмаса, көлем элементіндегі бөлшектердің саны кенет өзгеруі мүмкін) . Дәлірек айтсақ, гравитациялық F күштің кез-келген өзгерісі бұл күштің 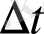уақыт ішіндегі әрекетінен болатын жылдамдықтың өзгерісінен баяу болу тиіс. Әрине, орташа гравитациялық өрістің өзгерісі бөлшектер қозғалысымен себептеледі, сондықтан аталған екі уақыт (күш пен жылдамдықтың өзгеріс уақыттары) шамамен бірдей болу тиіс деп көрінеді. Бірақ, орташа гравитациялық өріске бөлшектердің өте көп саны үлес қосатынына байланысты, бөлшектердің бір бөлігінің қозғалысы басқа бөлшектердің қозғалысымен теңеседі де, көптеген бөлшектердің қосынды өрісі кез-келген саны аз бөлшектерден тұратын элементтің үлесінен баяу өзгереді.