Біртексіз процестердің нормаланған информациялық энтропиясы

Пән: Математика, Геометрия
Жұмыс түрі: Реферат
Тегін: Антиплагиат
Көлемі: 3 бет
Таңдаулыға:

Біртексіз процестердің нормаланған информациялық энтропиясы.

Біртексіз процестер (біртексіз объектілер) үшін біз ұсынған өзқауымдастық критерилері $I_{1}, \ I_{2}$ -ден ерекшеленуі мүмкін. Объектің өзінің тепе-теңдігінен ауытқуды ескеретін кейбір параметрлердің әсерін елеу қажет.

Соңғы жылдары Цаллис статискасы немесе Гиббс квазиканондық статистикасы - жаңа жалпылама статистикалық механика дамуда [79, 80, 81] . Мұндай теориялар негізінде экспоненциалдық функция түріндегі қолдану жатады:

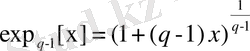(2. 38)

мұндағы 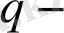біртектілік дәрежесі, статистикалық ансамбль толықсыздығының параметрі. өткенде біз қарапайым экспонентаны аламыз. Мағынасы бойынша:

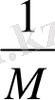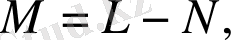
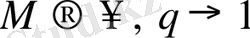~ , (2. 39)

мұндағы, тұйық жүйе бөлшектерінің саны, 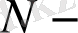жүйе ішіндегі бөлшектер саны. Гиббстың канондық таралуына сәйкес келетін статистиканың толықтығы 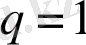болған кезде жетеді. Бірлікпен салыстырғанда 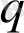параметрі зерттелетін жүйенің тепе-теңсіздігі мен біртексіздік статистика дәрежесін сипаттайды, ал зерттелетін физикалық өлшемнің тепе-теңсіздігі оның мәнінің ұяшыққа бөлуі арқылы сипатталады.

Кезкелген $x, y$ ансамбльдің біртектілік дәрежелі, жалпы энтропияны 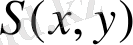анықтайық. Айнымалы ретінде бірөлшемді және шартты ықтималдылықтарды қолданайық: 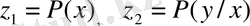. (2. 38) формулаға сәйкес:

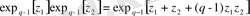(2. 40)

Сол жағын « 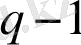логарифм» туындыдан қойсақ:

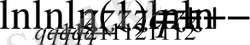(2. 41)

(2. 41) формуладан аддитивті емес 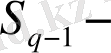энтропияның теңдігі шығады:

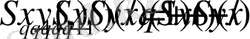(2. 42)

$q \rightarrow 1$ шегінде біз аддитивті энтропияны аламыз: $S(x, y) = S(x) + S\left( \frac{x}{y} \right)$ .

(2. 39) формуласындағы $q\$ анықталуына сәйкес, оны экспериментті мәндерден анықтауға болады. Геометриялық объектілердің біртексіздігін сипаттау үшін $q \approx 1$ параметрін енгіземіз. $q$ анықтау алгоритмін мына түрде жазамыз:

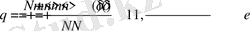0< 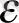<1 (2. 43)

мұндағы, 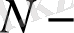нүктелердің (санақ) жалпы саны, 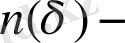бір нүкте болса болатын 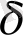сипаттамалық масштабты ұяшықтар саны, 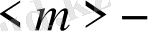ұяшықтағы нүктелердің орташа саны.

(2. 42) теңдікті қолдана отырып, біз информациялық энтропияның $q-\ ден\$ - тепе-теңсіз жүйенің анықталмағандығы мен күрделілігінің жалғыз өлшемінің қатынасын анықтайық. $q$ параметрімен сипатталатын квазитеңдік процестің информациясын мына түрде анықтаймыз:

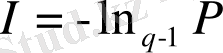(2. 44)

Информация реализациясының ықтималдылық таралу тығыздығының 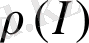функциясы былай анықталады:

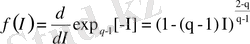(2. 45)

$S_{q}(I) = \int_{I}^{\infty}{If(I) dI} = (1 + I) \exp_{q - 1}( - I) = (1 + I) \left( 1 - (q - 1) I \right) ^{\frac{1}{q - 1}}$ (2. 46)

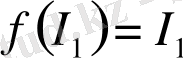және 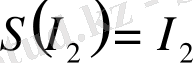өзұқсас мәндерді көріністің қозғалмайтын нүктелері ретінде табамыз:

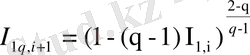(2. 47)

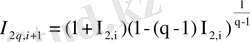(2. 48)

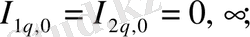
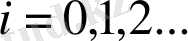
Осы арқылы $q$ параметрін өзұқсас пен өзаффиндік күйден жүйе ауытқуын информация мен информациялық энтропияның мәні ретінде сипаттаймыз.

q параметірінің мағынасын одан да әрі толықтыратын жәйт - мультифракталдық 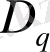өлшемділік пен Ренье 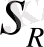энтропиясын ескеру. Яғни:

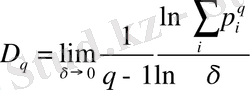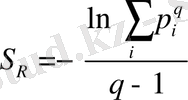, (2. 49)

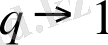кезінде Реньи 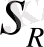энтропиясы мен Цаллис 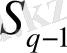энтропиясы (2. 42) Шеннон энтропиясына айналады. Осыдан 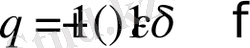кезінде бұл параметрді мультифракталдық моменттің бөлшек дәрежесі ретінде қарастыруға болады. Ал оны есептеу үшін (2. 43) қолдану q мәнін экспиремент жүзінде анықтауға мүмкіндік береді.

Ашық жүйе эволюциясының әмбебап энтропиялық заңдылықтары өзұқсас және өзаффиндік режимдерде (2. 47), (2. 48) формулаға сәйкес 2. 4 - суретте көрсетілген, сипаттамалық уақыт $t = i.$ Тепе-теңдіктен ауытқу $q < 1$ және $q > 1$ кезде орнатылған масштабтық инфарианттылықтың әр түрлі көрінісіне әкеледі. $q\$ параметрі энтропияның информациядан қатынасын өзгертеді (сурет 2. 4) .

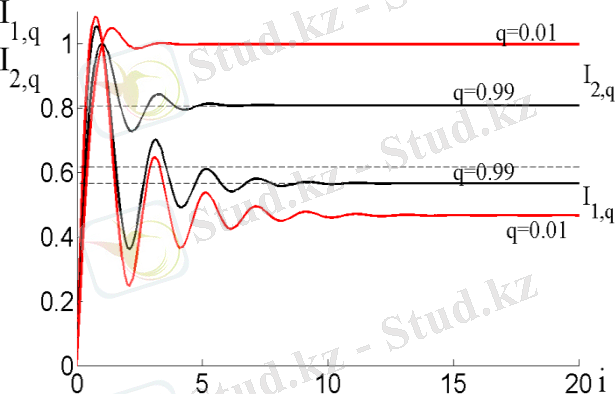
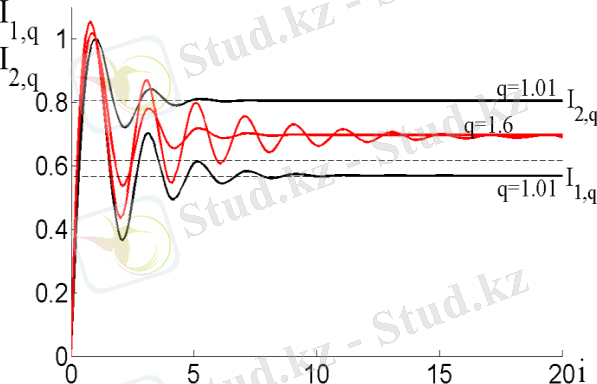
$C:\Users\Eskozha\Desktop\ENTROPY_ALL\article_2013\14112013\Seriiii\I22.tif$ $C:\Users\Eskozha\Desktop\ENTROPY_ALL\article_2013\14112013\Seriiii\II11.tif$