Ғарыш сәулелері арқылы мюонның өмір сүру уақытын бағалау және біртекті магнит өрісіндегі зарядталған бөлшектердің қозғалысы


ҒС көмегімен мюонның өмір сүру уақытын бағалау әдісі
Мюондар, өмір сүру уақыты τ μ = 2, 2*10 -6 с, спині s μ = h/2, массасы(m μ =105, 66МэВ/с 2 ) электронның массасынан 207 еседей артық, орнықсыз бөлшек. Олар нәзік әсерлесу салдарынан былай ыдырайды:
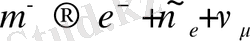
Осы ыдыраулар мюондардың вакуумдағы өмірінің ұзақтығын анықтайды. Заттарда μ - өмірі қысқарақ болады. Ол атомның оң зарядты ядросымен тартылып, онымен мюондық атом құрайды. Мюатомдардағы мюондар атом ядросымен қарпылуы мүмкін:
μ - + zA→ z - 1 A+ ν μ
Бұл құбылыс кәдімгі атомдағы К-қарпуға ұқсас, осыдан ол қарапайым μ - + р→n+ ν μ әсерлесуге сәйкес келеді.
Осының нәтижесінде теріс зарядты мюонның заттағы өмірі вакуумдағыға қарағанда жеңіл Z≈10 заттарда 2 есе, ауыр элементтерде 20-30 есе қысқарады.
ҒС-ң қатан (мюондық) құраушысының қарқындылығын тік сызыққа қатысты
Тыныштықтағы мюонның өмір сүру орташа уақыты
 өмір сүру уақытын көрсетеді, өйткені Эйнштейннің салыстырмалылықтың аранайы теориясы бойынша
өмір сүру уақытын көрсетеді, өйткені Эйнштейннің салыстырмалылықтың аранайы теориясы бойынша
мұндағы
Мюонның 1см жолдағы ыдырау ықтималдығы
W=1/ υ τ 0 /√1- β 2 =m 0 c/ m 0 υc/√1- β 2 * τ 0 = m 0 c/(pc) τ 0
мұндағы р ⋅ с - мезон энергиясы,
Санау жылдамдықтардың
бұдан
13. Зарядталған бөлшектің тұрақты біртекті магнит өрісіндегі қозғалысы
Зарядталған бөлшектің магнит өрісіндегі қозғалысы:
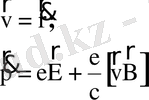 (3)
(3)
Зарядталған бөлшектің тұрақты біртекті магнит өрісіндегі қозғалысы
Ұйытқымаған қозғалыс
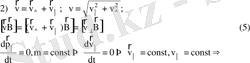
магнит өрісі бағытында бөлшек бірқалыпты қозғалады (магнит өрісі өзіне параллель бөлшектің қозғалысына әсер етпейді)
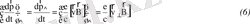
- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz