Біртектілік дәрежесін ескерген динамикалық жүйелердің информациялық энтропиясы


Жұмыс түрі: Материал
Тегін: Антиплагиат
Көлемі: 3 бет
Таңдаулыға:
Динамикалық жүйелердің энтропиясы
Динамикалық жүйенің бұрыннан белгілі талдауына біз ұсынып отырған жаңа әдісті қолданайық: логикалық бейнелеу [16], Хенон бейнелеуі, жинақ-шығарылу бейнелеуі, гомоклиникалық бифуркацияның дифференциалдық теңдеулер жүйесі және нейронды модельдің екіөлшемді бейнелеуі.
Фейгенбаум және Хенон бейнелеулері, сәйкесінше, мына түрде жазылады:
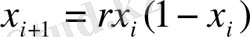 , (2. 4. 1)
, (2. 4. 1)
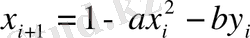 ,
,
 . (2. 4. 2)
. (2. 4. 2)
Гомоклиникалық бифуркацияның дифференциалдық теңдеулер жүйесі («желімдеу» немесе «gluingbifurcation» бифуркациясы) :
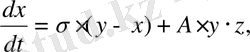
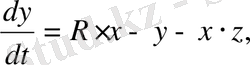
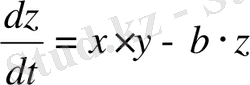 , (2. 4. 3)
, (2. 4. 3)
мұндағы
 ,
,
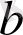 ,
,
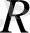 , А - параметрлер.
, А - параметрлер.
«жинақ-шығару»бейнелеуі:
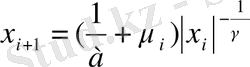 ,
,
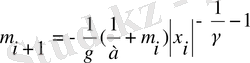 (2. 4. 4)
(2. 4. 4)
мұндағы γ - х i мәнінің фракталды өлшемділігінің бөлшектік бөлігі мағынасына ие, а - бақылау дәлдігі х i (0<1/ а <1) .
2. 3 сурет - Динамикалық жүйе эволюциясының энтропиялық заңдылықтары
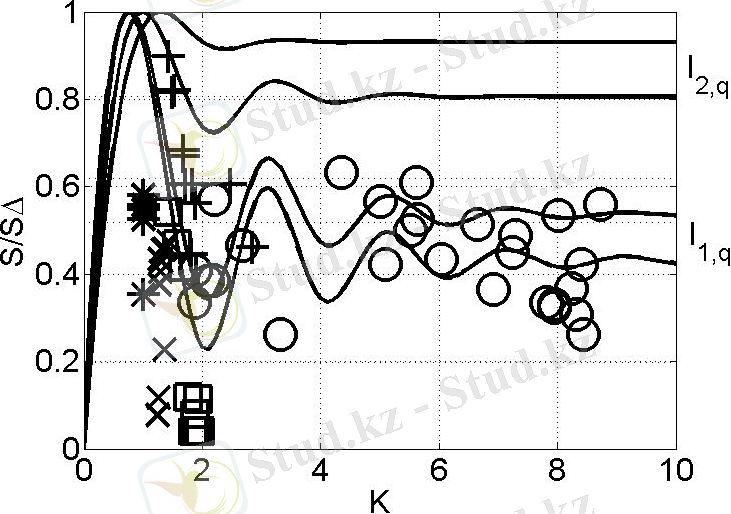
Гомоклиникалық бифуркация (+) (
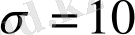 ,
,
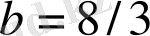 ,
,
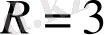 ,
,
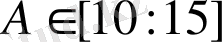 ), Алмастыру бейнеленуі (o) (
), Алмастыру бейнеленуі (o) (
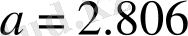 ,
,
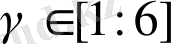 ), Рульков теңдеуі (*) (
), Рульков теңдеуі (*) (
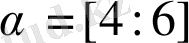 ,
,
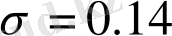 ,
,
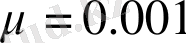 ), Логикалық бейнелеу (х) (
), Логикалық бейнелеу (х) (
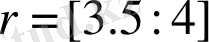 ) Хенон бейнелеуі () (
) Хенон бейнелеуі () (
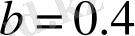 ,
,
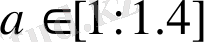 ) . Нүктелердің жалпы саны N=10
5
S
Δ
=17. 78. Суреттегі тұтас сызықтар теорияға сәйкес келеді.
) . Нүктелердің жалпы саны N=10
5
S
Δ
=17. 78. Суреттегі тұтас сызықтар теорияға сәйкес келеді.
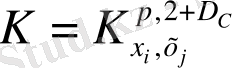 .
.
Нейронды модельдің екіөлшемді бейнеленуі:
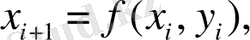
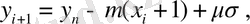 (2. 4. 5)
(2. 4. 5)
где
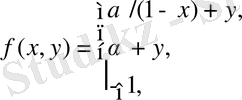
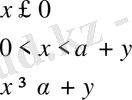 ,
,
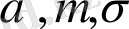 - параметрлер.
- параметрлер.
(41), (51) формулалары бойынша тұрғызылған жоғарыда келтірілген модельдердің информация - энтропиялы диаграммасы 19 - суретте көрсетілген.
2. 6 Біртектілік дәрежесі ескерілген екі өлшемді объекттің информациялық энтропиясы
Соңғы жылдары жаңа жалпыланған статистикалық механика дамуда [17 - 19], оны Цаллис статистикасы немесе Гиббстің квазиканоникалық статистикасы деп атауға болады. Мұндай теориялар негізінде мына экспоненциалды функцияларды қолдану жатыр:
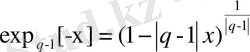 , (2. 5. 1)
, (2. 5. 1)
мұндағы
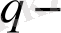 біртексіздік параметрі.
біртексіздік параметрі.
 шегінде біз қарапайым экспонентаны аламыз. Кіріспе бойынша :
шегінде біз қарапайым экспонентаны аламыз. Кіріспе бойынша :
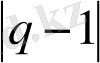 ~
~
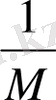 ,
,
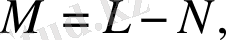
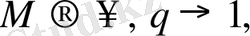 (2. 5. 2)
(2. 5. 2)
мұндағы
 тұйық жүйенің бөлшектер саны,
тұйық жүйенің бөлшектер саны,
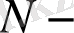 жүйешенің бөлшектер саны. Тепе-тең күйдегі Гиббстің каноникалық таралуына сәйкес келетін статистика толықтығы
жүйешенің бөлшектер саны. Тепе-тең күйдегі Гиббстің каноникалық таралуына сәйкес келетін статистика толықтығы
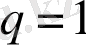 кезінде орын алады.
кезінде орын алады.
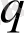 параметрінің бірден өзгешелігі жүйенің статистикалық тепе-теңділігінің дәрежесін, біртектілігін сипаттайды.
параметрінің бірден өзгешелігі жүйенің статистикалық тепе-теңділігінің дәрежесін, біртектілігін сипаттайды.
Біртектілік дәрежесін ескеріп,
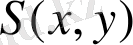 с толық энтропияны анықтайық. Айнымалы ретінде бірөлшемді және шартты
с толық энтропияны анықтайық. Айнымалы ретінде бірөлшемді және шартты
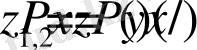 ықтималдықты қабылдайық :
ықтималдықты қабылдайық :
 . (2. 5. 3)
. (2. 5. 3)
Сол жақ бөлігін туындыдан «
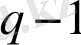 логарифм» ретінде қабылдап, мынаны аламыз:
логарифм» ретінде қабылдап, мынаны аламыз:
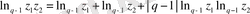 . (2. 5. 4)
. (2. 5. 4)
(40) формуладан аддитивті емес «
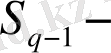 энтропия»:
энтропия»:
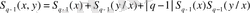 , (2. 5. 5)
, (2. 5. 5)
 шегінде
шегінде
 аддитивті энтропияға ие боламыз.
аддитивті энтропияға ие боламыз.
(38) формуласы бойынша
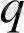 анықталуына сәйкес оны эксперименталды мәліметтерден анықтауға болады. Геометриялық объекттердің біртектілігін бейнелеу үшін кіші параметр енгіземіз:
анықталуына сәйкес оны эксперименталды мәліметтерден анықтауға болады. Геометриялық объекттердің біртектілігін бейнелеу үшін кіші параметр енгіземіз:
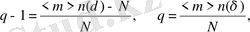 (2. 5. 6)
(2. 5. 6)
мұндағы
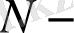 нүктелердің жалпы саны,
нүктелердің жалпы саны,
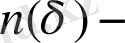
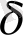 өлшеу масштабы бар ұяшықтар саны, онда тым болмағанда бір нүкте болады,
өлшеу масштабы бар ұяшықтар саны, онда тым болмағанда бір нүкте болады,
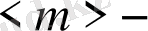 ұяшықтағы нүктелердің орташа саны.
ұяшықтағы нүктелердің орташа саны.
- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz