Жалпыланған фракталдық өлшемдер, корреляциялық өлшем және мультифракталдық спектр


Жұмыс түрі: Материал
Тегін: Антиплагиат
Көлемі: 6 бет
Таңдаулыға:
Евклид кеңістігіндегі өлшемі L фракталдық объектіні қарастырайық. Мұнда біз тек, бос емес, яғни ішінде кем дегенде бір нүктесі бар ұяшықтарды ескереміз. Бос емес ұяшықтардың i нөмері i = 1, 2, . . . N ( δ ) аралығында өзгерсін, мұндағы N ( δ ) ұяшықтың δ өлшеміне тәуелді - бос емес ұяшықтардың жалпы саны. Егер ұяшықтар бойынша нүктелердің таралуы бір келкі болмаса фрактал біртексіз, яғни мультифрактал ретінде қарастырылады. Мультифракталды сипаттау үшін ℒ облысындағы берілген нүктелердің таралуын сипаттайтын D q жалпыланған фракталдық өлшемділіктер енгізіледі.
n i (δ) -i-ші нөмерлі ұяшықтағы нүктелер саны болсын, онда
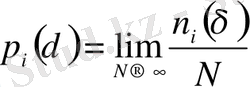
шамасы көп нүктелерден кездейсоқ алынған нүктелердің i -ші ұяшықта жататындығының ықтималдығы болып табылады. D q жалпылынған фракталдық өлшемділіктердің спектрі келесі қатынаспен анықталады:
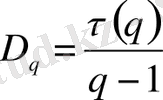 , (24)
, (24)
мұндағы
q
-
 <
q <+
<
q <+
 интервалында кез келген мәнді қабылдайды.
интервалында кез келген мәнді қабылдайды.
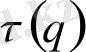 функциясы:
функциясы:
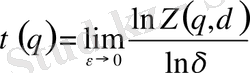 , (25)
, (25)
мұндағы
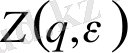 - жалпыланған статистикалық қосынды:
- жалпыланған статистикалық қосынды:
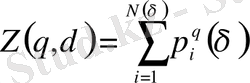 . (26)
. (26)
Егер
D
q
=
D
= const, яғни
q
-ға байланысты болмаса, бұл тек бір ғана шамамен -
D
фракталдық өлшемділікпен сипатталатын нүктелер жиыны жәй, регулярлы фрактал болады. Керісінше
D
q
функциясы
q
мен бірге өзгерсе онда қарастырылып отырған жиын мультифрактал болады.
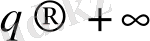 жағдайда (26) жалпыланған статистикалық қосындыға ең көп
n
i
бөлшектері бар ұяшықтар көп ықпал етеді, сондықтан олар ең көп
p
i
толтырылу ықтималдығымен сипатталады. Керісінше
жағдайда (26) жалпыланған статистикалық қосындыға ең көп
n
i
бөлшектері бар ұяшықтар көп ықпал етеді, сондықтан олар ең көп
p
i
толтырылу ықтималдығымен сипатталады. Керісінше
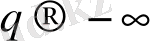 ұмтылғанда (26) жалпы статистикалық қосындыға ең аз толған ұяшықтар, яғни
p
i
-дің аз мәндері көп ықпал етеді. Осылайша,
D
q
функциясы, зерттеліп отырған
ℒ
нүктелер жиынының қаншалықты біртексіз екендігін көрсетеді
.
ұмтылғанда (26) жалпы статистикалық қосындыға ең аз толған ұяшықтар, яғни
p
i
-дің аз мәндері көп ықпал етеді. Осылайша,
D
q
функциясы, зерттеліп отырған
ℒ
нүктелер жиынының қаншалықты біртексіз екендігін көрсетеді
.
Жалпы жағдайда мультифрактал, статистикалық қосындының
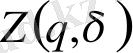 δ
→ 0 ұмтылғандағы қасиетін анықтайтын, қандайда бір
δ
→ 0 ұмтылғандағы қасиетін анықтайтын, қандайда бір
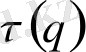 бейсызық
(25) функциямен сипатталады. Бірақ нүктелердін таралуын сипаттау үшін
бейсызық
(25) функциямен сипатталады. Бірақ нүктелердін таралуын сипаттау үшін
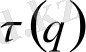 функциямен қатар оның туындысын да білу қажет:
функциямен қатар оның туындысын да білу қажет:
 (27)
(27)
Бұл туынды q мен бірге өзгереді.
q = 1 болғанда жалпыланған фракталдық өлшем:
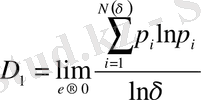 . (28)
. (28)
Бұл формуланың алымы, таңбасын ескергенде, фракталдық жиынның энтропиясы болып келеді (5-тарау, (8) формула) . Нәтижесінде D 1 жалпыланған фракталдық өлшем S ( δ ) энтропиямен келесі қатынаста болады:
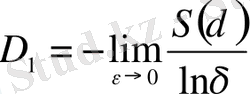 . (29)
. (29)
Бұдан,
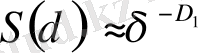 , (30)
, (30)
Яғни, D 1 дегеніміз нүктенің қандайда бір ұяшықта орналасу орнын анықтайтын информацияны сипаттайды. Осыған байланысты D 1 жалпы фракталдық өлшемділікті көп жағдайда информациялық өлшемділік деп атайды. Бұл δ ұяшықтың өлшемі нөлге ұмтылғанда, нүктенің орнын анықтау информациясы қалай өсетіндігін көрсетеді.
Корреляциялық өлшемділік
Бірдей өлшемді
δ
ұяшықтарға бөлінген фракталды бетті қарастырайық және кез-келген
х
1
және
х
2
еркін таңдалған екі нүкте фракталды объектіге жататын нүктелер болсын делік.
.
Екі нүктеніңде
i
-ші ұяшықта болу ықтималдығы қанша? Бір нүктенің осы беттің
i
-ші элементіне түсу ықтималдығы
р
i
-ге тең. Егер екі нүктенің осы ұяшыққа түсуі байланыссыз оқиғалар деп алсақ, онда оның ықтималдығы
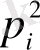 -ге тең болады.
-ге тең болады.
Фракталдық бет ( q = 2) жабылатын ұяшықтар көлемін кішірейткендегі, статистикалық қосындының (26) өзгерісін қарастырайық. δ -ны кішірейткенде қосынды азаяды, бұдан ол дәрежелік заңға бағынады деп жорамалдауға болады:
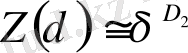 , (31)
, (31)
немесе, эквивалентті, шек
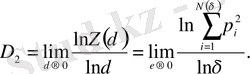 (32)
(32)
D 2 корреляциялық өлшемділік деп аталады.
Корреляциялық өлшемділіктің бейсызық динамикадағы ерекшелігі оны есептейтін салыстырмалы жеңіл және эффективті (басқа өлшемділіктерге қарағанда жеңіл және эффективті) тәсілі бар, ол - Грассбергер-Прокаччи алгоритмі .
Оның мағынасы мынандай. Біз динамикалық тендеуді сандық шешімдерінен күй вектор жиынын алдық делік {
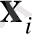 ,
i
= 1, 2, . . . ,
М
}, олар әрбір итерацияларға немесе дифференциалды тендеуді интегралдау қадамдарына сәйкес келсін. Қандайда бір (кіші)
δ
алып, корреляциялық өлшемділік анықтамасындағы бізге белгілі жиынды қолданып
,
i
= 1, 2, . . . ,
М
}, олар әрбір итерацияларға немесе дифференциалды тендеуді интегралдау қадамдарына сәйкес келсін. Қандайда бір (кіші)
δ
алып, корреляциялық өлшемділік анықтамасындағы бізге белгілі жиынды қолданып
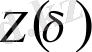 қосындысын бағалауға болады.
қосындысын бағалауға болады.
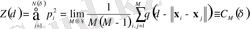 , (33)
, (33)
мұнда θ - сатылы Хевисайд функциясы:
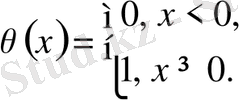 (34)
(34)
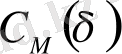 шамасын
корреляциялық интеграл
деп атайды.
шамасын
корреляциялық интеграл
деп атайды.
М
-ның үлкен мәндерінде (көбінесе мың немесе ондаған мың) ол
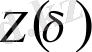 статистикалық қосындыны бағалауға мумкіндік береді, сондықтан оны корреляциялық өлшемділікті есептеуге қолдануға болады. Ол үшін
статистикалық қосындыны бағалауға мумкіндік береді, сондықтан оны корреляциялық өлшемділікті есептеуге қолдануға болады. Ол үшін
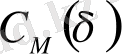 -ді өлшейді әртүрлі
δ
-да есептейді, шешімін
-ді өлшейді әртүрлі
δ
-да есептейді, шешімін
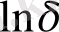 және
және
 координаттарында салады.
координаттарында салады.
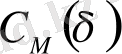 тәуелділігі
тәуелділігі
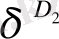 болса, алынған график бұрыштық коэффициенті
D
2
-ге тең түзу сызық болу керек.
болса, алынған график бұрыштық коэффициенті
D
2
-ге тең түзу сызық болу керек.
Корреляциялық интегралды (33) -ші формула арқылы есептеу үшін есептеу көлемі өте көп болады, себебі есептеу саны М 2 пропорционал . Оны азайту үшін «аздаған қулықтар» қолданылады.
Біріншіден, қарастырылып отырған фазалық көлемді бірнеше бөлікке бөліп және сол бөлікке сәйкес
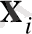 нүктелерін әр топ бойынша қарастыруға болады. Егер
δ
кіші (бізге қажеттті) болса, онда корреляциялық интегралды есептегенде тек екеуі де бір топта жататын нүктелерді ғана есепке алуға болады.
нүктелерін әр топ бойынша қарастыруға болады. Егер
δ
кіші (бізге қажеттті) болса, онда корреляциялық интегралды есептегенде тек екеуі де бір топта жататын нүктелерді ғана есепке алуға болады.
Екіншіден, евклидті норманың орнына, есептеу санын аз қажет ететін басқа норманы қолдануға болады. Өлшемділіктің шамасы алынған норма түріне байланысты емес. Нормалар тобын енгізейік:
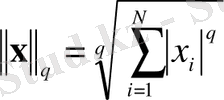 , (35)
, (35)
Мұндағы
q -
параметр, айталық,
q
= 2 евклидті нормаға сай. Олардың ішіндегі ең ыңғайлы және тез шешілетін нормалар
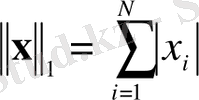 и
и
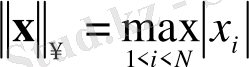 .
.
 болғандықтан, есептеу санын екі есе азайтуға болады. Ол үшін (33) орнына келесі формуланы қолдануға болады:
болғандықтан, есептеу санын екі есе азайтуға болады. Ол үшін (33) орнына келесі формуланы қолдануға болады:
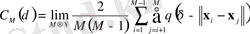 . (36)
. (36)
Практикада логарифмдік координаттарда тұрғызылған корреляциялық интегралдың графигі, δ -ның үлкен мәндерінде (атракторлардың өлшемімен салыстырмалы болғанда), және өте кіші δ үшін (жақсы статистикалық баға беруге қажетті жұп нүкте саны азайғанда), түзу сызықтан ауытқиды. Есептеу көлемі М көбейген сайын, түзу сызық интервалы кең бола бастайды . Көп жағдайда оны көз өлшеммен алып, алынған нүктелерді орташа квадрат әдіс бойынша аппроксимациялық түзу алу үшін өндейді. 11- суретте логикалық бейнелеу (логистическое отображение) үшін есептелінген логарифмдік координаттардағы корреляциялық интегралдың δ- ға байланысты графигі көрсетілген.
% Корреляциялық өлшемділік байланысын есептейтін
%файл-бағдарламаның листингі
Nx = 100;
% init input signal
X = zeros(Nx, 1) ;
r = 4;
x = 0. 1;
for i=1:50
x = fotbr(x, r) ; % функцияны шақырады
%логикалық байланыс fotbr
% (файл-функцияның анықтамасы 4-ші тарауда)
end;
X(1, 1) = x;
clear x;
for i=2:Nx
X(i, 1) = fotbr(X(i-1, 1), r) ;
end;
clear r;
% init input signal end
Ne = 60; % 45
eps = zeros(1, Ne) ;
Corr = zeros(1, Ne) ;
he = 0. 1;
eps (1) = 0. 01;
Corr (1) = C(X, eps(1) ) ;
e_he = exp(he) ;
for j = 2:Ne
eps(j) = eps(j-1) * e_he;
Corr(j) = C(X, eps(j) ) ;
end;
ln_eps = log(eps) ;
ln_Corr = log(Corr) ;
D=(Ne*sum(ln_eps. *ln_Corr) -sum(ln_eps) …
*sum(ln_Corr) ) /(Ne*sum(ln_eps. ^2) -…
sum(ln_eps) ^2) ;
plot(ln_eps, ln_Corr, 'k. ') ;
xlabel('ln(\epsilon) ') ;
ylabel('ln(C) ') ;
title(' логикалық бейнелеу үшін …
Корреляциялық өлшемділік ') ;
D
% корреляциялық өлшемнің сан мәні
% камандалық бағанаға шығарылады MatLab.
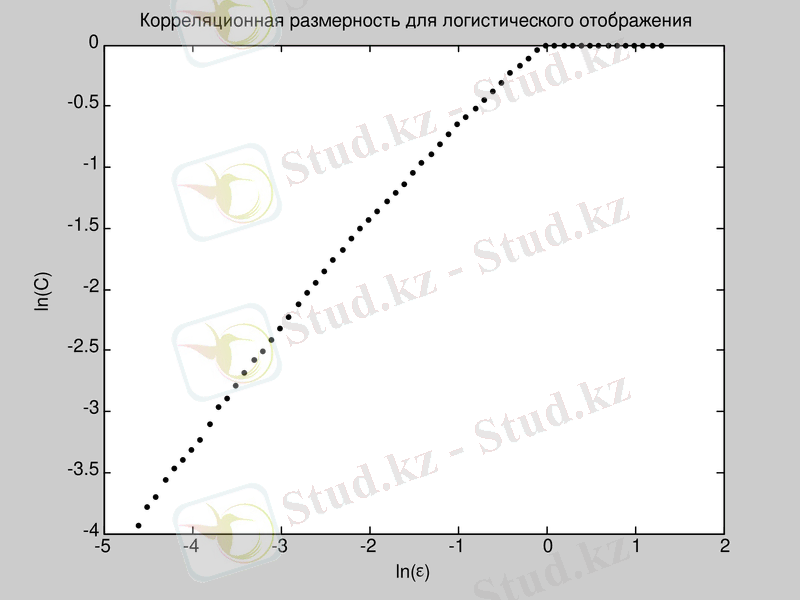
11-сурет. Логикалық бейнелеу үшін корреляциялық өлшемділік D = 0. 7131
Тапсырмалар
1. Параметрлері μ = 1. 0, b = 0. 3, B = 1. 0, ω = 1. 5 болатын сыртқы қозуы бар Ван-дер-Поль тендеуінің (1-ші тарау (13) -теңдеу) корреляциялық өлшемділігін есептеңіз.
2. Параметрлері μ = 1. 0, b = 0. 3 Ван-дер-Поль генераторының (1-ші тарау (12) -теңдеу) корреляциялық өлшемділігін есептеңіздер. Алдындағы есептін жауабымен салыстырыңыз. Айырмашылықты түсіндіріңіз.
Мультифракталды спектрлік функция f(α)D q шамасы жалпы қабылданған мағынасында нақты айтатын болсақ фракталдық өлшемділік емес. Сондықтан көп жағдайда мультифракталды жиынды бейнелеу үшін мультифракталды спектрлік функция f ( α ) (мультифракталдың сингулярлығының спектрі) қолданылады. Біз f ( α ) шамасы ℒ жиынындағы біртекті фракталдық ішкі жиынының хаусдорф өлшемділігіне (2) тең екендігін көрсетеміз .
Өзұқсас жиын үшін р i шамасының δ ұяшық өлшеміне тәуелділігі дәрежелік байланыста болады
 (37)
(37)
мұндағы α i - қандайда бір дәрежелік көрсеткіш (шынында әр-түрлі i ұяшыққа әр-түрлі) . Регулярлы (бірқалыпты) фракталдар үшін α i дәрежелік көрсеткіштер бірдей және D фракталдық өлшемділікке тең
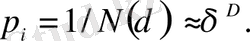 (38)
(38)
Бұл жағдайда (26) статистикалық қосынды келесі түрге өзгереді
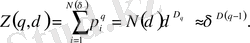 (39)
(39)
Сондықтан
 және барлық жалпыланған фракталдық өлшемділіктер
D
q
=D
бұл жағдайда бір-біріне сәйкес келеді және
q
-ға байланысты емес
.
Бірақ мультифрактал сияқты күрделі объектілер үшін
р
i
ұяшықтардың толтырылу ықтималдығы бірдей емес және
α
i
дәреже көрсеткіші әр-түрлі. Көп кездесетін жағдайдың бірі - осы мәндер қандайда бір (
α
min
,
α
max
) жабық интервалды толтырады және
және барлық жалпыланған фракталдық өлшемділіктер
D
q
=D
бұл жағдайда бір-біріне сәйкес келеді және
q
-ға байланысты емес
.
Бірақ мультифрактал сияқты күрделі объектілер үшін
р
i
ұяшықтардың толтырылу ықтималдығы бірдей емес және
α
i
дәреже көрсеткіші әр-түрлі. Көп кездесетін жағдайдың бірі - осы мәндер қандайда бір (
α
min
,
α
max
) жабық интервалды толтырады және
 . (40)
. (40)
- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz