Үздіксіз сигналдың энтропиясы

Пән: Математика, Геометрия
Жұмыс түрі: Материал
Тегін: Антиплагиат
Көлемі: 4 бет
Таңдаулыға:

Үздіксіз сигналдың энтропиясы

Үздіксіз сигнал энтропиясы шексіздікке тең, себебі шексіз көп нүктеден алынатын информация және оның логарифмі шексіздікке тең. Дегенмен, дискретті сигналдарға қатысты энтропия ұғымын үздіксіз сигналға жалпылайық.

Үздіксіз сигналды үздіксіз кездейсоқ шама х ретінде қарастырайық. р ( х ) ықтималдық тығыздығын кванттау процесіне сәйкес дискретті шамаға ауыстырамыз (2-сурет) . Ықтималдық тығыздығы немесе х кездейсоқ шамасының ықтималдығының таралу тығыздығы деп 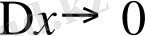жағдайдағы ( х - ∆х /2, х + ∆х /2) интервалына түскен х шамасының ∆х- қа қатынасын айтады.

2-сурет. Кездейсоқ шаманың ықтималдығының таралу тығыздығы

Р _k

p ( x )

x _i - ∆ x _i /2 x _k x _i + ∆ x _i /2

p ( x )

Олай болса к- сыншы күйдің ықтималдылығы келесі түрде анықталады:

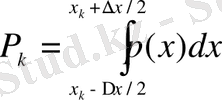Үздіксіз кванттық сигнал энтропиясы мына түрде болады:

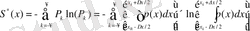Жеткілікті аз ∆х және р ( х ) жазық функция болғанда (орта мән теоремасы бойынша) төмендегіше есептеуге болады:

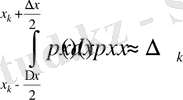нөлге ұмтылған шекте бастапқы үздіксіз сигналдың энтропиясын аламыз:

(13)

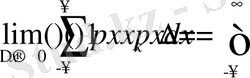Күткеніміздей ∆x →0 кванттық сигналдың энтропиясы шексіздікке ұмтылады. Бір қарағанда алынған нәтиже қанағаттаналарлық, пайдалы болып көрінуі мүмкін: егер сигналдың энтропиясы шексіз үлкен болса, онда оның көмегімен шексіз информация мөлшерін беруге болады! Бұл үшін жүйе күйіне сәйкес априорлы анықталмағандықты алып тастау жеткілікті. Бірақ, анықталмағандықты толық алып тастау деген не? Бұл қабылданған сигналдың абсолютты дәл мәнін алу деген сөз, бірақ бұны нақты жағдайларда жүзеге асыру мүмкін емес. Үздіксіз сигнал әрқашан шектелген дәлдікпен жуықтап қабылданады.

Осылайша, үздіксіз сигналдардың энтропиясының абсолютты өлшемі жоқ. Сондықтан оларға жаңа түсінік салыстырмалы энтропияны енгізеді, яғни х үздіксіз сигналдың энтропиясын басқа бір x ′ үздіксіз сигналға қатысты анықтайды.

Эталон ретінде ε интервалында бірқалыпты таралу заңы бар x ′ үздіксіз сигнал таңдалады. (13) -формула мұндай сигнал үшін мына түрде жазылады:

өйткені

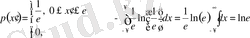басқа жағдайларда;

мұндағы е - кезкелген сан болсын.

Үздіксіз шама х- тің анықталмағандығы x және x ′ энтропияларының айырмасы ұмтылатын санмен сипатталады:

Егер е = 1 деп алсақ (яғни бірлік интервалда бірқалыпты таралу заңы бар стандартты шама үшін (эталон) ), онда формула мына түрді қабылдайды:

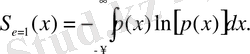
Бұл үздіксіз сигналдың абсолютты емес энтропиясының мөлшері екендігін түсіну керек. Бұл салыстырмалы энтропия, мұнда стандарт ретінде бірлік интервалда біркелкі таралған шама алынған. Кейде оны дифференциалды ε энтропия деп те атайды. Егер х ' сигналының басқа таралу заңын алатын болсақ, онда х сигналының салыстырмалы энтропиясының өрнегі де басқа түрде жазылады.

Үздіксіз сигналдың салыстырмалы энтропиясы көп жағдайда дискретті сигнал энтропиясының қасиеттеріне ұқсас. Бірақ айырмашылықтары да бар. Мысалға, дискретті сигналдың энтропиясы тек ықтималдыққа ғана тәуелді және сигнал мәнінің өзіне тәуелді емес (ол сигналдардың таралу заңдылығына толық тәуелді емес) . Үздіксіз сигналдың салыстырмалы энтропиясы жалпы жағдайда таралу заңына толығымен тәуелді. Бұл «толығымен» деген сөз, оның энтропиясы сигналдың тұрақты құраушысына тәуелді еместігін ескереді.

Сонымен, үздіксіз сигналдың салыстырмалы энтропиясының бірінші қасиетін тұжырымдайық: егер сигналға кездейсоқ емес с шамасын қоссақ, онда үздіксіз сигналдың салыстырмалы энтропиясы өзгермейді . Расында, егер х сигналының мәндерінің таралуы 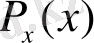болса, онда сигналдың таралуы у=х+с -ға тең болады және у сигналының энтропиясы төмендегі өрнекпен анықталады:

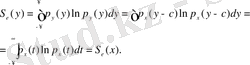
Үздіксіз сигналдардың энтропиясының экстремальды қасиеттері. Кейбір параметрлері белгілі қандай да бір хабарлама немесе сигналдар ансамбілі берілсін. Мысалға, өзгеру аралығы, дисперсиясы, математикалық күтімі (орта мәні) берілсін.

Кездейсоқ шаманы жуықтап сипаттау үшін моменттер деп аталатын сандық сипаттамалар енгізіледі. Бірінші реттегі бастапқы момент математикалық күтім деп аталады :

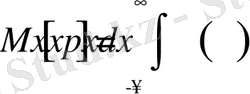мұндағы р ( х ) - кездейсоқ шаманың үлестірілу функциясы. Дискретті кездейсоқ шамалар үшін

мұндағы р ( х _i ) - кездейсоқ шамасының пайда болу ықтималдығы.

Математикалық күтім кездейсоқ шаманың байқалуының орта мәнін сипаттайды.

Екінші ретті орталық момент дисперсия деп аталады

Дисперсия кездейсоқ шаманың өзінің математикалық күтімінің маңайындағы мүмкін болатын мәндерінің байқалу дәрежесін сипаттайды. Дисперсияның квадраттық түбірі σ = квадраттық ауытқу деп аталады .