Кодтау әдістерінің жіктелуі және кедергіге төзімді сызықтық екілік кодтар теориясы


Жұмыс түрі: Курстық жұмыс
Тегін: Антиплагиат
Көлемі: 16 бет
Таңдаулыға:
Мазмұны
Кіріспе
1 Кодтау әдістерінің классификациясы
2 Кодтау әдістерінің сыныптамасы
3 Кедергіге төзімді кодтау каналы
4 Дәлдігі мен қателерін түзету үшін сызықты бинарлы кодтау
Қорытынды
4
5
7
10
12
19
Кіріспе
“Сигнал” термині тек ғылыми-техникалық сұрақтарда ғана емес, күнделікті өмірде жиі кездеседі. Сигналды-хабар, информация деп қабылдауға да болады. “Сигнал” сөзі латынның “signum”-“белгі беру” сөзінен шыққан.
Сигнал деп мәліметті көрсететін, қабылдайтын немесе беретін кез-келген бір объектінің уақыт бойынша физикалық күйінің өзгеруін айтады. Хабар, информация көптеген инженер, математиктер мен . 40-шы жылдарыК. Шеннонинформация теориясының
бастапқытарауын бітіреді.
Сигналдарды кез-келген физикалық процестер сияқты электрондық оссциллограф, вольтметрлер, қабылдағыштар сынды приборлар және құрылғылармен зерттеуге болады. Сигналдарды теориялық жағынан ұғыну мен есептеудің объектісі ретінде қарастыру үшін, сол сигналдың математикалық моделін көрсету керек.
Сигналдың математикалық моделі, мысалы, аргументі уақыт болып табылатын функционалдық тәуелділік болып табылады.
модель ток, кернеу, т. б. -нысуреттейді.
Сигналдарды суреттейтін функциялар заттық, сонымен қатар, комплекстік мәндерге ие болады.
Сигналдардың математикалық моделін біле отырып, оларды бір-бірімен салыстырып, айырмашылығын көруге болады.
Радиотехникаға қатысты сигнал болып кез-келген бір тізбектің қысқыштарының арасындағы кернеу немесе өткізгіштегі ток болып табылады. Бір уақыт функциясымен сипатталатын мұндай сигналды бірөлшемді деп атайды. Бірақ, кейде көпөлшемді немесе векторлы сигналдарды қарастыру ыңғайлы.
Кодтау (кодирование; coding; кодировать; encode) - мәліметтерді олардың алдын ала тағайындадған бейнелеу немесе мәліметтер элементін (символдар жиынын) олардың кодтық комбинацияларымен сәйкес келтіру, программалау процесі.
1Кодтау әдістерінің классификациясы
Осы тарауда қарастырылған кодтау әдістерінің жіктелуі 1-суретте көрсетілген. Бұл жіктеу толық емес. Ол қазіргі заманғы байланыс жүйелерінде кеңінен қолданылатын кейбір әдістерді ғана қамтиды. Оның тағайындалуы бойынша кодтау қарабайыр (примитивное) , экономдық және кедергіге тұрақты болып бөлінеді.
Қарабайыр (примитивные) - кодтау бастапқы алфавитке және арна әліпбиіне сәйкестендіру үшін пайдаланады.
1-кестеде келтірілген мысалда K = 4 алфавитінің көлемі бар дискретті көзден алынған хабарламалардың дискретті екілік арна арқылы қалай трансляциялауға болатындығы көрсетілген.
Сурет-1 Кодтау әдістерінің классификациясы.
Примитивтік кодтау ақпараттарды шифрлау және үндестіру жүйесінің тұрақтылығын арттыру үшін қолданылады. соңғы жағдайда, кодтау ережесі тек нөлдерден немесе тек біреуден тұратын ұзын тізбектің шығу коэффициентінің пайда болу ықтималдығы аз болуынан сәйкес келеді. Осыган ұқсас кодер скремблер деп аталады ( ағл. «Scramble» - араластыру) .
1-кесте
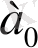

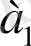

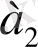
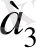
Экономды кодтау немесе деректерді қысу, ақпаратты сақтау уақытын немесе сақталған кезде қажетті жад көлемін азайту үшін пайдаланылады. Экономикалық кодтаудың айырықша қасиеті мынада, бұл көзден тыс, кодердің шығуымен құралған кодер кірісіндегі көздің артық болуынан аз. Экономикалық кодтау компьютерлерде қолданылады. Осылайша, операциялық жүйелердің соңғы нұсқаларында олардың композициялық деректерді қысу бағдарламалары болуы тиіс және жалпы қолданыстағы телефондық желілердегі компьютерлер арасындағы байланыс үшін модемдерге арналған жаңа V. 42bis стандарты деректерді өңдеу процедураларының санына қысқарады.
Бейсызық немесе шамадан тыс кодтау дискретті арнада жіберілген кезде пайда болатын қателерді анықтау және / немесе түзету үшін пайдаланылады. Кедергіге төзімді кодтаудың айрықша ерекшелігі - бұл кодектердің шығуымен туындаған көздің артықшылығы код кірісінде көздің артық болуынан. Кедергіге төзімді кодтау әртүрлі байланыс жүйелерінде, компьютерлік желілерде, тұтынушымен және кәсіби дыбыстық және бейнематериалдарда сандық жазба негізінде деректерді сақтау және беру кезінде пайдаланылады.
2 Кодтау әдістерінің сыныптамасы
Хабарлама көздерін кодтаудың көптеген жолдары бар. Көптеген әдістер практикада жүзеге асырылады, әсіресе, факсимильді және телевизиялық хабарларды бірнеше есе қысқартуға мүмкіндік береді, онда олар сізге бірнеше рет хабарларды беру жылдамдығын арттыруға мүмкіндік береді. Бұл бөлімде алдымен белгілі хабарламалар статистикасы бар көздерді кодтау қарастырылады. Мұндай кодты құрудың жалпы идеясы кодтаудың теоремасы 1 кедергісіз арналар үшін туындады. Код тізбегінің орташа ұзындығы азайтылғандықтан, код тең емес болуы керек. Арна символдарының неғұрлым қысқа комбинациялары ықтимал бастапқы хабарлармен қамтамасыз етілгенде, біркелкі емес кодының орташа ұзақтығы азайтылады. Алайда, қабылдаушы жақтың біркелкі емес коды осы комбинациялардың шекараларына белгісіз болып шығады. Егер оларды танымал кодтау әдісімен оқшаулауға тырыссақ, декодтау екі жақты болуы мүмкін. Бірегей декодталғандығының қасиеті болуы үшін қолданылатын код үшін белгілі бір шарттарды қанағаттандыруы керек. Егер басқа кодтық жазудың бастамасы болмаса, бір таңбалы декодтау қамтамасыз етіледі. Мұндай кодтар префикс деп аталады.
Префикс кодының болуы үшін қажетті және жеткілікті шарттар Крафт теңсіздігімен анықталады, оны біз теорема түрінде тұжырымдаймыз.
Теорема 1.
 - кедергісіз дискретті арна алфавитінің көлемі болсын,
- кедергісіз дискретті арна алфавитінің көлемі болсын,
 оң бүтін сандардың соңғы жиынтығы. Міндеттің префикс кодының ұзындығы
оң бүтін сандардың соңғы жиынтығы. Міндеттің префикс кодының ұзындығы
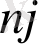 ,
,
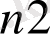 , . . . ,
, . . . ,
 ,
,
 бар болуы үшін келесі теңсіздікті қанағаттандыру қажет:
бар болуы үшін келесі теңсіздікті қанағаттандыру қажет:
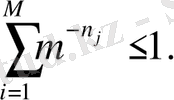
Келтірілген жеткілікті дәлелдемелер. Жиын
 теңсіздікті қанағаттандырады. (1)
теңсіздікті қанағаттандырады. (1)
Ошибка перевода. Бұл түрдегі теңсіздікті қайта жазамыз
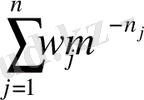
Мұндағы
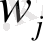 - ұзындық тізбектерінің саныjжәне nmax
- ұзындық тізбектерінің саныjжәне nmax
Осы соманы кеңейте отырып, біз бұл теңсіздікті өзгертеміз
(2)
Өйткені барлық wj - теріс емес, онда оның (2) теңсіздік жүйесін табамыз
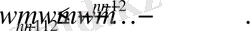
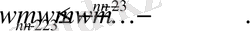
.
 (3)
(3)
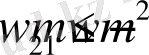
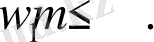
Бұл теңсіздік жүйесі кодын код ұзындығының осы жиынтығымен кодтау әдісін анықтайды. Біріншіден,
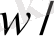 ұзындығы
ұзындығы
 сөзді таңдаймыз, осы мақсат үшін көлемі m алфавитінен түрлі әріптерді қолданамыз. Қолданбалы рәміздер жоқ, сондықтан біз ұзындығы
сөзді таңдаймыз, осы мақсат үшін көлемі m алфавитінен түрлі әріптерді қолданамыз. Қолданбалы рәміздер жоқ, сондықтан біз ұзындығы
 сөзді құрай аламыз
сөзді құрай аламыз
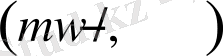 оларға
оларға
 көлемінің алфавитіненсимволы қосамыз. Осы сөздерден
көлемінің алфавитіненсимволы қосамыз. Осы сөздерден
ұзындығы
 ,
,
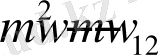 «еркін» префикс болып табылатын ерікті сөздерді таңдаймызұзындығы
«еркін» префикс болып табылатын ерікті сөздерді таңдаймызұзындығы
 . Осы префикстерге алфавиттің әртүрлі рәміздерін қосу арқылы ұзындығының
. Осы префикстерге алфавиттің әртүрлі рәміздерін қосу арқылы ұзындығының
 сөзін
сөзін
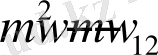 аламыз, солардан біз еркін сөздерді таңдаймыз және т. б. Осылайша жалғастыра отырып, біз Кофтегі теңдеуді қанағаттандыратын префикс кодын жасап шығарамыз (1) .
аламыз, солардан біз еркін сөздерді таңдаймыз және т. б. Осылайша жалғастыра отырып, біз Кофтегі теңдеуді қанағаттандыратын префикс кодын жасап шығарамыз (1) .
Енді, § 6. 1-ге сәйкес, оның A алфавитінің
 - дан ерекше белгілері мен символдардың пайда болу ықтималдығы
- дан ерекше белгілері мен символдардың пайда болу ықтималдығы
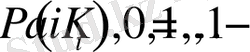 анықталған жадсыз дискретті хабарламалардың кейбір көздерін қарастырайық. Егер осы көзден берілген рәміздердің тізбегі ұзындығы n блоктарына бөлінсе, онда осы блоктың әрқайсысы жаңа көздің символы ретінде қаралуы мүмкін, онда
анықталған жадсыз дискретті хабарламалардың кейбір көздерін қарастырайық. Егер осы көзден берілген рәміздердің тізбегі ұзындығы n блоктарына бөлінсе, онда осы блоктың әрқайсысы жаңа көздің символы ретінде қаралуы мүмкін, онда
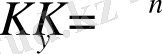 көлемінің үлкен әліпбиі және ең алғашқы символдардың ықтималдығы
көлемінің үлкен әліпбиі және ең алғашқы символдардың ықтималдығы
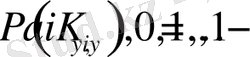 ретінде анықталған символдардың пайда болуы ықтималдығы осы блокта. Теорема 7. 1-де сипатталған біркелкі емес кодтың n-блоктарының ұзындығын анықтаймыз:
ретінде анықталған символдардың пайда болуы ықтималдығы осы блокта. Теорема 7. 1-де сипатталған біркелкі емес кодтың n-блоктарының ұзындығын анықтаймыз:
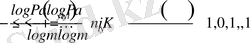 (4)
(4)
Сонда (4) біз оны аламыз,
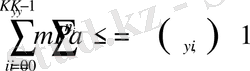 ,
,
демек, 1-теорема арқылы біз ұзындығы , ұзындығы бар кедергісіз mари арна символдарының тізбесін кеңейтілген алфавитпен көздің рәміздерімен байланыстыра аламыз. Содан кейін осындай тізбектің орташа ұзындығы үшін
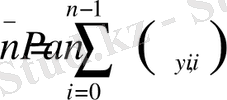
теңзіздігі жүзеге асады
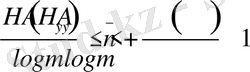 .
.
Ескертусіз дереккөз үшін
 және, сонымен бірге, бұл мәнді бір көздің белгісіне жатқызамыз
және, сонымен бірге, бұл мәнді бір көздің белгісіне жатқызамыз
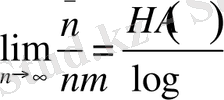 . (5)
. (5)
Шындығында, кодтау теоремасын жадсыз жадсыз арналар үшін дәлелдеп берді. Сонымен қатар, ол шекті мән орташа ұзындығы дәлелдеді және (4) бар сәйкесітше таңдалған ұзындығы тен емес префикс коды реттілігін пайдалана кодтау арқылы алынуы мүмкін. Бұл префикс кодын қалай жасауға болатынын көрсету қажет. Префикс қасиеті бар бірыңғай емес кодтарды жасау үшін бірнеше алгоритмдер бар. Олардың ішінде оңтайлы, яғни. бұл шексіз лимитке (5) жақындауға мүмкіндік береді, Хаффмен алгоритмі [8] . Алайда, біз бұл жерде көп жағдайда бірдей нәтижелері әкеледі қарапайым алгоритмі Шеннон-Фано, қарастыру.
Шаннон-Фано алгоритмі келесідей. Бастапқы әліпбидің (бастапқы немесе кеңейтілген) рәміздері ықтималдығы жоғарылау тәртібімен жазылады. Содан кейін олар екі бөлікке бөлінеді, сондықтан осы бөліктерге кіретін таңбалардың ықтималдығы шамамен бірдей болады. Бірінші бөлімнің барлық рәміздері нөлге тең емес кодының бірінші таңбасы ретінде белгіленеді және екінші бөліктің рәміздері бір тағайындалады. Содан кейін осы бөліктердің әрқайсысында (егер ол бірнеше хабарламадан тұратын болса) екіге бөлінеді, мүмкін теңдестірілмейтін бөліктер және сол кодтау ережесі оларға қолданылады. Бұл процесс алынған бөліктердің әрқайсысында бір хабарлама қалмайынша қайталанады.
3 Кедергіге төзімді кодтау каналы
Егер экономикалық кодтау хабарлардың қайнар көздерінің артық болуын азайтса, шу-иммундық кодтау, керісінше, коммуникациялық арнада берілу кезінде туындайтын қателерді анықтауға және (немесе) түзетуге қабілетті болу үшін мақсатты енгізуді білдіреді.
Болашақта біз тек арна (шуылға қарсы иммундық) кодтауды қарастырамыз, бірақ жалпы тәсіл қолдануға болады, сонымен қатар, ол әсіресе үздіксіз сигналдарды дискретті түрде жіберген кезде өте маңызды әсерге ие болады (8-тарауды қараңыз) .
Енді біз блоктық кодтардың жалпы теориясын ұсынамыз. Біз ұзындығы n, арна (шуылға қарсы иммундық) блоктық код

әрқайсысы алфавитті енгізудің
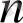 -нің кез-келген мағынасын қабылдай алады
-нің кез-келген мағынасын қабылдай алады
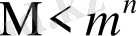 . (6)
. (6)
Бұл кодты да артық деп атайды. Егер
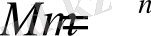 теңдігі қанағаттандырылса, код примитив деп аталады. Кодекс нормасын шақырамыз
теңдігі қанағаттандырылса, код примитив деп аталады. Кодекс нормасын шақырамыз
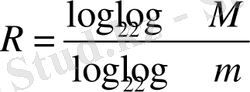 ; егер
; егер
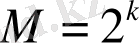 (7)
(7)
Әлбетте, артық коды
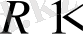 , ал қарабайыр коды үшін
, ал қарабайыр коды үшін
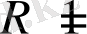 .
.
Шеннон кодтау теоремасы, алдыңғы тарауда дәлелдеді
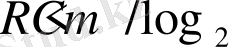 тіркелген мөлшерлемемен блок резервтеу кодтар тізбегі бар екенін, мұнда
тіркелген мөлшерлемемен блок резервтеу кодтар тізбегі бар екенін, мұнда
 - өткізу жолағын байланыс арнасы, осы блок қате ықтималдығы
- өткізу жолағын байланыс арнасы, осы блок қате ықтималдығы
 шексіз ұлғайтуға ұзындығы деп осы арнадағы оңтайлы декодтау нөлге бейім болады. Алайда, осы тарауда біз жағдайда, яғни айналысатын тіркелген ұзындығы
шексіз ұлғайтуға ұзындығы деп осы арнадағы оңтайлы декодтау нөлге бейім болады. Алайда, осы тарауда біз жағдайда, яғни айналысатын тіркелген ұзындығы
 кодтары, сондықтан практикалық маңызы бар проблемаларды, жаңа жиынтығы бар:
кодтары, сондықтан практикалық маңызы бар проблемаларды, жаңа жиынтығы бар:
1. Үздік кодты және оптикалық декодтауды пайдалану кезінде қате ықтималдығын білдіретін код блокінің ұзындығының функциясы,
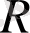 кодының жылдамдығы және байланыс арнасы арқылы анықталған қателік ықтималдығын бөлу.
кодының жылдамдығы және байланыс арнасы арқылы анықталған қателік ықтималдығын бөлу.
2. Берілген коды мен арнаны түзету немесе қателерді анықтау арқылы оңтайлы декодтау алгоритмін табыңыз.
3. Берілген арнадағы оңтайлы декодтау үшін ең жақсы кодты таңдау әдісін табыңыз.
4. Шифрлау және декодтау үшін практикалық алгоритмдерді жасау.
Осы уақытқа дейін байланыс арнасы арқылы жіберілетін рәміздердің тізбегі бір-біріне тәуелсіз кодтау құрылғысы арқылы қалыптастырылған сегменттерге (блоктарды) бөлуге болатын блоктық кодтар туралы мәселе ғана болды. Бұл әдіс жалғыз мүмкін емес. Демек, үздіксіз (конволитациялық) деп аталатын кодтар осы тараудың екінші бөлігінде сипатталады. Бірінші бөлімнің соңында, тек қана кодты блоктауға арналған, түсіндіріледі, неге және дәл үздіксіз кодтар блоктық кодтардан белгілі бір артықшылықтарға ие болуы мүмкін.
Кедергіге төзімді: блок және үздіксіз кодтар.
Бір критерий үшін оңтайлы кодты таңдау (табу) мәселесін шешу немесе кодтау теориясының мәні болып табылады. Айта кету керек, қазіргі заманғы кодтау әдісі байланыс арнасының әлеуетті өткізу қабілетін жақындауға мүмкіндік бермейді, сонымен қатар жоғары берілудің жоғары дәлдігі. Дегенмен, құзыретті кодты іріктеу, көптеген жағдайларда, арнаның өткізу қабілетінің тәртібіндегі беру жылдамдығы кезінде қате қабылдау ықтималдығын едәуір азайтуға мүмкіндік береді.
Қазіргі кезде кедергі бар арналарда берілудің сенімділігін жоғарылату қателерді анықтайтын немесе түзететін кодтар арқылы жүзеге асырылады. Бұл кодтау кептеліске төзімді деп аталады. Бұл жағдайда, код тізбектілігінің артық болуы хабардың көзінің артық болуына қарағанда жоғары. Осыған байланысты қабылдау қателерін анықтауға және түзеуге болады.
Біркелкі емес кодтар арқылы бастапқы кодтаудың тікелей және кері теориялары.
Тікелей кодтау теоремасы, кез келген бірегей декодталған код үшін, екілік кодты сөз таңбаларын орташа сандағы хабар көзінің энтропиясына кем екенін мәлімдейді
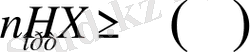 , және бірегей декодталған коды бар, ол үшін теңсіздік
, және бірегей декодталған коды бар, ол үшін теңсіздік
 қолданылады.
қолданылады.
Кері кодтау теоремасы теңсіздікті
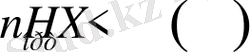 қанағаттандыратын бірегей декодталған кодты құру мүмкін еместігін дәлелдейді.
қанағаттандыратын бірегей декодталған кодты құру мүмкін еместігін дәлелдейді.
Осы теоремалардан хабарды кодтаудың орташа ұзындығы хабардың бойымыздағы ентропасынан аз екенін дәлелдеу мүмкін емес. Сонымен қатар, кодтаудың орташа ұзындығы хабар көзінің бойымыздан біршама айырмашылығы болады. Әрбір хабардың таңбасын кодтамасаңыз және әріпінің X түріндегі таңбалар блоктары болмаса, әр хатқа арналған код таңбаларының орташа саны азайтылуы мүмкін. Блоктық кодтауды пайдаланып, бір хабарламаға орташа санын аламыз, бұл көздің энтропиясынан мүлдем аз ерекшеленеді, бірақ кодтаудың күрделілігін артырады.
4 Дәлдігі мен қателерін түзету үшін сызықты бинарлы кодтау
Мұнда біз тек екілік кодтарды сипаттауға шектеліп отырмыз, өйткені бұл математикалы аппарат ретінде соңғы өрістер теориясы ретінде қазіргі заманғы алгебраның күрделі бөлігін қолдануды талап етпейді. Алайда, осы тараудың соңында, мұнда анықталған барлық ұғымдар мен қасиеттер m-ary кодтарының жағдайына қалайша ұзартылатынын атап өткіміз келеді.
Анықтау 11.
Ұзындығы
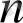 -ның сызықтық блоктың екілік коды
-ның сызықтық блоктың екілік коды
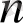 - нөлдік нөлдік тізбекті қамтитын ұзындығы
- нөлдік нөлдік тізбекті қамтитын ұзындығы
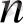 -ның екілік тізбектерінің жиынтығы және осы жиынтыққа тиесілі тізбектердің әрбір жұбы үшін олардың битальды сомасының
-ның екілік тізбектерінің жиынтығы және осы жиынтыққа тиесілі тізбектердің әрбір жұбы үшін олардың битальды сомасының
 -модулі де осы жиынның элементі болып табылады . (Соңғы сипатты биттік қосу
-модулі де осы жиынның элементі болып табылады . (Соңғы сипатты биттік қосу
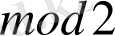 қатысты жабық деп атауға болады. )
қатысты жабық деп атауға болады. )
Мысал.
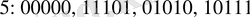 ұзындықтарының тізбегі тікелей тексерілуі мүмкін сызықтық кодты құрайды.
ұзындықтарының тізбегі тікелей тексерілуі мүмкін сызықтық кодты құрайды.
 -ші және
-ші және
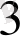 -ші комбинациялардың бит сомасы
-ші комбинациялардың бит сомасы
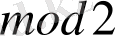 4-ші комбинацияны береді,
4-ші комбинацияны береді,
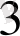 және
және
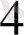 -сомалар
-сомалар
 -ді береді, ал
-ді береді, ал
 және
және
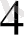 -сомалар 3-комбинациясын береді. Сызықтық кодтың ұзындығы n-ның барлық екілік тізбегінің
-сомалар 3-комбинациясын береді. Сызықтық кодтың ұзындығы n-ның барлық екілік тізбегінің
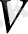 кеңістігі үшін
кеңістігі үшін
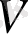 сызықтық подпространства анықтамасы қанағаттандыратыны анық (немесе топтың жұмыс модулінің қосылуы
сызықтық подпространства анықтамасы қанағаттандыратыны анық (немесе топтың жұмыс модулінің қосылуы
 -модуліне қатысты барлық екілік «топтардың топтары үшін кіші топ болып табылады) . Сондықтан, екілік сызықтық кодтар тобы. )
-модуліне қатысты барлық екілік «топтардың топтары үшін кіші топ болып табылады) . Сондықтан, екілік сызықтық кодтар тобы. )
Алгебрадан соңғы сан (
 ) элементтерден тұратын әр-өлшемді сызықтық подпространство н-өлшемді кеңістіктің негізін, яғни, сызықтық тәуелсіз элементтердің жиынтығы, олардан
) элементтерден тұратын әр-өлшемді сызықтық подпространство н-өлшемді кеңістіктің негізін, яғни, сызықтық тәуелсіз элементтердің жиынтығы, олардан
 битальды жиынтықтау модулін қолданып, осы ішкі кеңістіктің кез-келген элементтерін құруға болады, яғни, бұл жағдайда сызықтық кодының тіркесімі. Мұндай ішкі кеңістіктің барлық негіздері подпространство өлшемін анықтайтын элементтердің бірдей санынан тұратындығын дәлелдеді.
битальды жиынтықтау модулін қолданып, осы ішкі кеңістіктің кез-келген элементтерін құруға болады, яғни, бұл жағдайда сызықтық кодының тіркесімі. Мұндай ішкі кеңістіктің барлық негіздері подпространство өлшемін анықтайтын элементтердің бірдей санынан тұратындығын дәлелдеді.
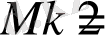 сызықтық кодының жалпы саны, себебі бұл
сызықтық кодының жалпы саны, себебі бұл
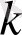 негізіндегі элементтердің мүмкін болатын битальды сомаларының жалпы саны, және олардың арасында негіздердің элементтерінің желілік тәуелсіздігіне байланысты екі бірдей сома болмауы керек.
негізіндегі элементтердің мүмкін болатын битальды сомаларының жалпы саны, және олардың арасында негіздердің элементтерінің желілік тәуелсіздігіне байланысты екі бірдей сома болмауы керек.
Сызықтық тәуелсіз жолдар түрінде жазылған база элементтерінің жиынтығы кодтың генераторлық матрицасы деп аталатын екілік матрицаны құрайды:
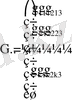 (7)
(7)
G арқылы жасалынатын барлық код сөздерінің жиынтығы ұсынылуы мүмкін
ретінде:
 (8)
(8)
мұнда x - өлшемнің n сөздік кодының векторы; b - ұзындық k ақпараттық символдарының векторлық жолдары. (8) формула матрицаға көбейтіледі, ал барлық іс-шаралар
 режимінде жүзеге асырылады. Әлбетте,
режимінде жүзеге асырылады. Әлбетте,
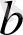 векторы ретінде екілік дерек көзімен алынған хабардың дәйекті элементтеріне қолдана аласыз. Көптеген жалпы кодтардан желілік кодтарға көшу кодтау күрделілігінің мәселесін іс жүзінде шешеді. Шындығында,
векторы ретінде екілік дерек көзімен алынған хабардың дәйекті элементтеріне қолдана аласыз. Көптеген жалпы кодтардан желілік кодтарға көшу кодтау күрделілігінің мәселесін іс жүзінде шешеді. Шындығында,
 ұзындығының
ұзындығының
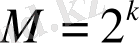 комбинациясын еске түсірудің орнына, яғни,
комбинациясын еске түсірудің орнына, яғни,
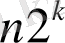 биттері жалпы жағдайда,
биттері жалпы жағдайда,
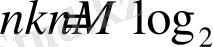 биттерден тұратын генераторлық матрицаны ғана есте сақтау қажет. Осындай кодтау процедурасы
биттерден тұратын генераторлық матрицаны ғана есте сақтау қажет. Осындай кодтау процедурасы
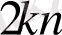 қарапайым операцияларды орындауды қажет етеді.
қарапайым операцияларды орындауды қажет етеді.
Сызықтық кодтарға көшу оларды табу және түзету қабілеттерін талдауды (және, тиісінше, тапсырманы) айтарлықтай жеңілдетеді. Шынында да,
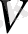 болсын - комбинациялары бар сызықтық екілік код
болсын - комбинациялары бар сызықтық екілік код

мұндағы
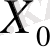 - нөлдік комбинация. Содан кейін сызықтық кодының жабық сипаты бойынша
- нөлдік комбинация. Содан кейін сызықтық кодының жабық сипаты бойынша
кез келген жұп нөлдік комбинациялар үшін (
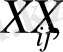 ) Хамминг арасындағы қашықтық
) Хамминг арасындағы қашықтық
олар Хаммина салмағына тең болады
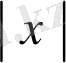 нөлден басқа бір кодқа жататын кейбір үшінші комбинация. Сондықтан кез-келген сызықтық код үшін ең төмен кодты алудың маңызды қорытындысы бар
нөлден басқа бір кодқа жататын кейбір үшінші комбинация. Сондықтан кез-келген сызықтық код үшін ең төмен кодты алудың маңызды қорытындысы бар
қашықтық
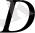 нөлге қоспағанда, код сөз бар ең төменгі Хемминга салмағы, болып табылады.
нөлге қоспағанда, код сөз бар ең төменгі Хемминга салмағы, болып табылады.
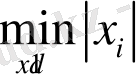 (9)
(9)
Осылайша, барлық сызықтық кодтар үшін Хамминг аралығындағы жұп комбинациялар арасындағы қашықтықты зерттеу Хаммингтің салмақтарының тізімін зерттеуге тең, бұл айтарлықтай оңайырақ.
Кейбір генерациялайтын матрица
 арқылы берілген кез-келген сызықтық коды үшін келесі сипат да айқын: кез-келген бағандар мен оларды ауыстыру немесе біріктіру кезінде қосылатын жолдардың қарапайым түрлендіруі осы кодтың салмақтарының тізімін өзгертпейді. Екінші жағынан, мұндай трансформациялардың көмегімен кез келген
арқылы берілген кез-келген сызықтық коды үшін келесі сипат да айқын: кез-келген бағандар мен оларды ауыстыру немесе біріктіру кезінде қосылатын жолдардың қарапайым түрлендіруі осы кодтың салмақтарының тізімін өзгертпейді. Екінші жағынан, мұндай трансформациялардың көмегімен кез келген
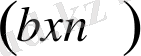 сызықтық тәуелсіз жолдармен екілік матрица G канондық түрге дейін қысқартылуы мүмкін.
сызықтық тәуелсіз жолдармен екілік матрица G канондық түрге дейін қысқартылуы мүмкін.
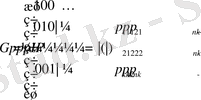 (10)
(10)
мұнда
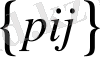 - кейбір екілік элементтер; - бірыңғай матрица
- кейбір екілік элементтер; - бірыңғай матрица
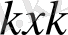 (басқа диаграммадағы негізгі диагональдар мен нөлдердегі бірлікпен) ;
(басқа диаграммадағы негізгі диагональдар мен нөлдердегі бірлікпен) ;
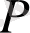 - екілік элементтерден тұратын
- екілік элементтерден тұратын
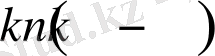 матрицасы;
матрицасы;
 және
және
 матрицаларын дәйекті жазуды білдіреді.
матрицаларын дәйекті жазуды білдіреді.
Функцияны (8) матрицаны G (10) түрінде пайдалану арқылы аламыз
(11)
Мұнда
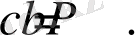
Матрица көбейту ережесі бойынша біз
 үшін аламыз.
үшін аламыз.
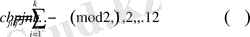
Оның формуладағы канондық матрицада (10) анықталған сызықтық коды арқылы кодтау процедурасы екі дәйекті сөзден тұратын код сөзін қалыптастыруға азайтатынын және бірінші қосалқы сөздің ұзындығы
 ұзындығының ақпараттық дәйектілігіне сәйкес келетінін білдіреді (11) және (12) хабарлардың көзі, екіншісі матрица
ұзындығының ақпараттық дәйектілігіне сәйкес келетінін білдіреді (11) және (12) хабарлардың көзі, екіншісі матрица
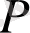 сызықтық комбинациясы арқылы қалыптасады.
сызықтық комбинациясы арқылы қалыптасады.
Анықтама 12. Сөздері (11) түрінде ұсынылатын сызықтық кодтар жүйелі деп аталады.
Біз, әрине, әрбір сызықтық коды салмақтардың тізбесін және демек, Хаммэн қашықтықтарын сақтау тұрғысынан жүйелі түрде бірдей болатындығын көрсеттік. Кілт сөздердің алғашқы белгілеріне көздің рәміздерімен сәйкес келеді, олар ақпараттық болып табылады, ал соңғы n - таңбалар тексеріледі. Бұдан бұрын
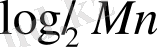 ретінде анықталған код жылдамдығы, -line коды үшін k / n тең болады, яғни, жүйелі - ақпараттық нышандар санының кодын блоктың ұзындығына ара қатынасы n ұзындығы n және ақпараттық таңбалар саны бар жүйелік кодтар қысқаша кодтар
ретінде анықталған код жылдамдығы, -line коды үшін k / n тең болады, яғни, жүйелі - ақпараттық нышандар санының кодын блоктың ұзындығына ара қатынасы n ұзындығы n және ақпараттық таңбалар саны бар жүйелік кодтар қысқаша кодтар
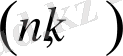 деп аталады. Кейде мұндай код үш параметрмен белгіленеді, мұндағы
деп аталады. Кейде мұндай код үш параметрмен белгіленеді, мұндағы
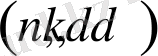 - ең төменгі код аралығы.
- ең төменгі код аралығы.
Сызықтық алгебрада ортогоналды кеңістік немесе сызықтық кеңістік үшін нөлдік кеңістік туралы ұғым бар. Анықтау бойынша, кез келген
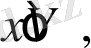 үшін
үшін
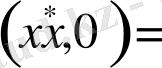 ұзындығының
ұзындығының
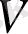 векторларының жиынтығы. Tиісті векторлардың скалярлық өнімін білдіреді. (Біздің жағдайда барлық операциялар
векторларының жиынтығы. Tиісті векторлардың скалярлық өнімін білдіреді. (Біздің жағдайда барлық операциялар
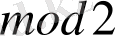 орындалады) . Бұл жинақ әрдайым сызықтық кеңістік екендігін дәлелдейді, ал егер
орындалады) . Бұл жинақ әрдайым сызықтық кеңістік екендігін дәлелдейді, ал егер
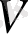 коды dimension
коды dimension
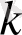 болса,
болса,
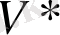 кодының өлшемі
кодының өлшемі
 болады, яғни
болады, яғни
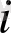 . Ортогоналды кеңістікке сәйкес келетін
. Ортогоналды кеңістікке сәйкес келетін
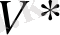 коды
коды
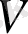 кодының қосарлы деп аталады. Ол сондай-ақ оның генерациялайтын матрицасы
кодының қосарлы деп аталады. Ол сондай-ақ оның генерациялайтын матрицасы
 өлшемімен
өлшемімен
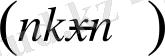 болады. Сонан соң
болады. Сонан соң
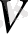 бастапқы кодының векторлық-матрицалық теңдеудің шешімі ретінде анықталуы мүмкін
бастапқы кодының векторлық-матрицалық теңдеудің шешімі ретінде анықталуы мүмкін
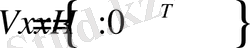 (13)
(13)
мұндағы T - матрица H , яғни трансфозиттік белгісі. жолдар мен бағандарды өзара ауыстыру. Х* матрицасы V* коды үшін генератор, бастапқы код үшін тексеру матрицасы деп аталады, K матрицасы H сияқты G сияқты канондық түрде [21] ұсынылуы мүмкін және оны
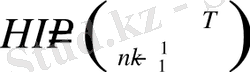 (14)
(14)
мұндағы
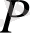 - ұсыныста көрсетілгендей матрица (10) .
- ұсыныста көрсетілгендей матрица (10) .
Сызықтық кодтардың теориясында біз ең төменгі d қашықтыққа арналған шекараларды табамыз.
ТЕОРЕМ 7. 7. Плоткиннің жоғарғы шекарасы.
Егер код блогының ұзындығы
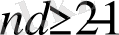 болса, онда
болса, онда
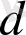 мәніне жету үшін сызықтық кодтың минималды қашықтығы үшін қажетті
мәніне жету үшін сызықтық кодтың минималды қашықтығы үшін қажетті
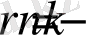 таңбалар саны кем дегенде
таңбалар саны кем дегенде
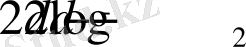 болады. (Дәлелді [21] -дан табуға болады. ) Соның салдарынан,
болады. (Дәлелді [21] -дан табуға болады. ) Соның салдарынан,
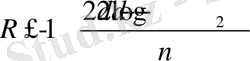
ТЕОРЕМ 7. 8. Варшамов-Гилберттің төменгі шекарасы.
Төмендегі теңсіздікті қанағаттандыратын төменгі қашықтыққа ие (n, k) -код бар:
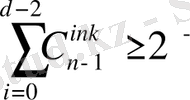 (15)
(15)
- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz