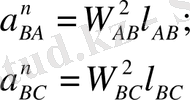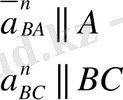Жазық механизмдердің кинематикалық зерттелуі: орналасу, жылдамдықтар және үдеулер жобалары


Қорқыт Ата атындағы Қызылорда мемлекеттік университеті
Тақырыбы: Жазық механизмдердің кинематикалық зерттеуі
Орындаған:
Қабылдаған:
Қызылорда, 2016ж
Жоспар :
I Кіріспе
II Негізгі бөлім
1) Механизмның орналасу жобасы
2) Жазық механизмдердің жылдамдықтар және үдеулер жобасы
3) Ассур топтарының жылдамдықтарын және үдеулерін анықтау
4) Жазық механизмдердің кинематикалық зерттеуінде графикалық және аналитикалық әдістерді қолдану
III Қорытынды
Кіріспе
Кинематикалық талдауда механизм звеноларының қозғалысын зерттеуіне әсер ететін күштерді ескермейді. Осыған байланысты кинематикалық зерттеуді келесідей есептеулер жүзеге асырылады:
а) Механизм орнының және нүктелерінің траекториясын анықтау.
б) Механизм нүктелерінің және звеноларының жылдамдығын, бұрыштық жылдамдығын анықтау
в) Механизм нүктелерінің және звеноларының үдеуін, бұрыштық үдеуін анықтау.
Механизмнің қозғалысы периодты түрде қайталанып тұрады, сондықтан оның жетекші звеносының бір толық айналымына сәйкес келетін бір периодтағы қозғалысын зерттеу жеткілікті.
Звенолардың қозғалысы жетекші звеноның қозғалысына тәуелді, сондықтан кинематикалық талдауды алдын ала берілуі керек:
- Өлшемдерді көрсетіле отырып механизмнің құрылымдық сұлбасы (кинематикалық сұлба)
- Бастапқы звеноның қозғалыс заңы
Кинематикалық талдаудың негізгі әдістері:
- жобаларды құру әдісі
- кинематикалық диаграмма әдісі
- аналитикалық әдіс
Механизмдерді Ассур топтарына жіктей отырып кинематикалық зерттеуді барлық механизм үшін емес, оның жекелеген бөліктеріне жүргізуге болады. Бұл кинематикалық зерттеуді жеңілдетеді.
Машиналар және механизмдер теориясында механизмдерді зерттеу графикалық әдіс арқылы жүзеге асырылады. Графикалық әдіс көптеген механизмдерді зерттеу үшін жарамды, қарапайым және кейбір механизмдерді зерттеу үшін қолданылатын бірде-бір әдіс.
Механизмнің звеноларының өлшемдерін және нүктелерінің жылдамдықтарын, үдеулерін графикалық түрде салғанда масштабтық коэффициенттерді қолданады.
Масштабтық коэффициент деп қандай да бір физикалық шаманың нақты мәнінің осы шаманы сызбада миллиметрмен кесінді ұзындығы арқылы көрсететін мәнге қатынасын атайды. Масштабтық коэффициенті
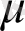 әріпімен белгіленеді және индекс арқылы қай шамаға байланысты алынғанын көрсетеді.
әріпімен белгіленеді және индекс арқылы қай шамаға байланысты алынғанын көрсетеді.
Ұзындықтың масштабтық коэффициенті
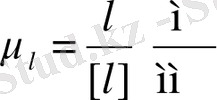 . Мұндағы
l
- шаманың нақты мәні, [
l
] -
l
шамасын сызбада көрсететін кесіндік ұзындығы.
. Мұндағы
l
- шаманың нақты мәні, [
l
] -
l
шамасын сызбада көрсететін кесіндік ұзындығы.
Жылдамдықтың масштабтық коэффициенті
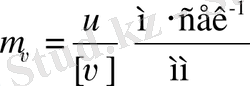 .
.
Үдеудің масштабтық коэффициенті
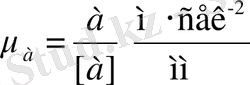 .
.
Масштаб және масштабтық коэффициент өзара кері шама болып табылады. Мысалы масштаб
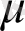 1:5 болса, онда масштабтық коэффициент
1:5 болса, онда масштабтық коэффициент
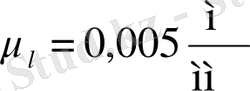 тең болады.
тең болады.
Механизмның орналасу жобасы
Механизмнің кинематикалық сұлбасын бастапқы звеноның белгілі бір орнына сәйкес салу механизмнің орналасу жобасы деп аталады. Механизм орналасу жобасын салу үшін мысал қарастырайық.
1. Төртзвенолы топсалы механизм.
Механизмнің орналасуын келесідей реттпен жүргізледі:
а) Нүкте қозғалысының белгілі траекториясын саламыз. Кривошип ОА ценрті О нүктесі болып табылатын шеңбер бойымен бірқалыпты бұрыштық жылдамдықпен айналады. Сондықтан А нүктесінің орны кез келген уақыт аралығында белгілі (ОА звеносының кез келген бұралуы бұрышында) . Радиусы ОА-ға тең шеңберді алты бөлікке бөлеміз. Сонан кейін А 1 , А 2 , . . . , А 6 нүктелермен белгілейміз. В нүктесі центрі С нүктесі болып табылатын радиусы СВ-ға тең шеңбер бойымен радиусы СВ-ға тең доға жасай отырып, қозғалады. Доғаның бойына А 1 , А 2 , . . . , А 6 нүктелерінен радиусы АВ-ға тең шатунның ұзындығын өлшеп саламыз. Аынған А 1 , және В 1 , А 2 және В 2 , . . . , сол сияқты В 1 және С 1 , В 2 және С 2 . . . , нүктелерін өзара қосамыз. Осылай кривошиптің бір айналымына (қозғалыс циклін) сәйкес келетін шатуын және күйенте орындарын анықтаймыз.
Күйентенің сағат тіліне қарама-карсы жүрісі жұмыс жүрісіне, ал сағат тіліне бағыттас бос жүріске сәйкес келеді.
2. Кривошипті-текті механизм Кривошип және шатун бір сызық бойында орналасқан. Қозғалмайтын О центрі бойынша айналатын, радиусы ОА-ға тең шеңберді тең бөліктерге бөлеміз. Алынған нүктелерді А 1 , А 2 , . . . , А 6 әріптермен белгілейміз. Осы нүктелер бойнша тиектің қозғалатын өсі бойынша А 1 В 1 , А 2 В 2 , . . . , А 6 В 6 шатунның ұзындықтарын өлшеп саламыз. Табылған В 1 , В 2 , В 3 нүктелері поршеньнің (тиектің) жұмыс жүрісіне, ал В 4 , В 5 бос жүрісіне сәйкес келеді.
Жазық механизмдердің жылдамдықтар және үдеулер жобасы
Механизмдердің жылдамдықтар және үдеулер жобасы деп механизм звеноларының әртүрлі нүктелерінің қарастырып отырған жағдайдағы жылдамдықтары мен үдеулерінің бағыты мен шамасын векторлық кесінді ретінде көрсетілетін сызбасын айтады.
Жылдамдықтар және үдеулер жобасын салғанда алдын ала берілуі керек:
а) звенолардың өлшемдері б) механизмнің орналасу жобасы
в) жетекші звеноның бұрыштық жылдамдығы
Кинематикалық зерттеуде графикалық әдістерді қолдану үшін жылдамдықтар және үдеулер векторларының бағыты жеткілікті болу қажет. Сонымен қатар әртүрлі жағдайларды қарастырғанда жылдамдықтар және үдеулер үшін векторлық теңдеулерді құра білу керек.
1. Звено ілгерлемелі қозғалыс жасайды.
Звено ілерлеиелі қозғалыс жасағанда оның нүктелерінің жылдамдықтары, үдеулері шамасы жағынан тең және бағыттары бірдей болады.
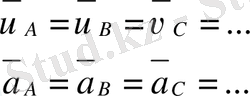
2. Звено қозғалмайтын өсь бойымен айналмалы қозғалыс жасайды.
Бұл жағдайда А нүктесінің жылдамдығы
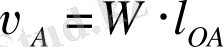 . Жылдамдық векторы радиуске перпендикуляр және бұрыщтық жылдамдықтың бағытына сәйкес анықталады.
. Жылдамдық векторы радиуске перпендикуляр және бұрыщтық жылдамдықтың бағытына сәйкес анықталады.
А нүктесінің нормаль үдеуінің шамасы
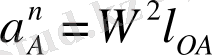 немесе
немесе
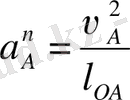
Нормаль үдеу векторы әрқашанда радиус бойынша айналу центріне қарай бағытталған (А нүктесінен О нүктесіне қарай) . А нүктесінің жанама үдеуінің шамасы
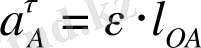
Жанама үдеу векторы радиуске перпендикуляр және бағыты бұрыштық үдеудің бағытымен сәйкес келеді. А нүктесінің толық үдеуі
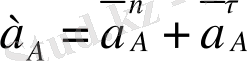 немесе
немесе
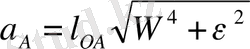 .
.
А нүктесінің үдеу векторының радиустан ауытқу бұрышы
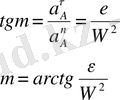
немесе
3. Екі нүкте бір звеноның бойында жатады және арақашықтықтары
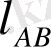 -ға тең
-ға тең
В нүктесінің жылдамдығы бізге теориялық механика курсынан белгілі. Жылдамдықтары қосу туралы теореманы қолданамыз. В нүктесінің абсолютты жылдамдығы (
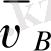 ) . Осы нүктенің тасымалдау (
) . Осы нүктенің тасымалдау (
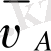 ) және салыстырмалы (
) және салыстырмалы (
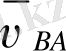 ) жылдамдықтарының қосындысына тең.
) жылдамдықтарының қосындысына тең.
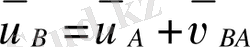 мұндағы
мұндағы
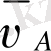 - А нүктесінің жылдамдық векторы,
- А нүктесінің жылдамдық векторы,
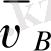 - В нүктесінің жылдамдық векторы,
- В нүктесінің жылдамдық векторы,
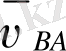 - А нүктесіне байланысты алынған В нүктесінің жылдамдығы. В нүктесінің А нүктесі бойымен айналу жылдамдығы
- А нүктесіне байланысты алынған В нүктесінің жылдамдығы. В нүктесінің А нүктесі бойымен айналу жылдамдығы
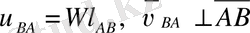
мұндағы
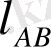 - А және В нүктелерінің нақты арақашықтғы (масштабтық шама емес) . Онда бұрыштық жылдамдық
- А және В нүктелерінің нақты арақашықтғы (масштабтық шама емес) . Онда бұрыштық жылдамдық
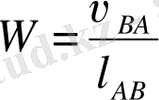
 бағыты бұрыштық жылдамдық векторының айналу бағыты бойынша анықталады. В нүктесінің абсолютті үдеуі (
бағыты бұрыштық жылдамдық векторының айналу бағыты бойынша анықталады. В нүктесінің абсолютті үдеуі (
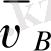 ), тасымалдау үдеуі (
), тасымалдау үдеуі (
 ) және салыстырмалы үдеулердің (
) және салыстырмалы үдеулердің (
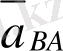 ) қосындысынан тұрады.
) қосындысынан тұрады.
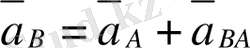
мұндағы салыстырмалы үдеу екі үдеуден тұрады - нормаль (
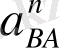 ) және жанама үдеу (
) және жанама үдеу (
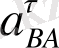 )
)
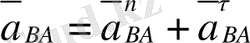
онда В нүктесінің үдеуі
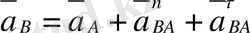
А нүктесіне байланысты алынған В нүктесінің нормаль үдеуі, В нүктесінен А нүктесіне қарай бағытталған (айналу центріне) . Оның шамасы
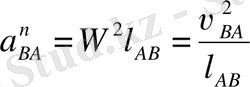
Жанама үдеу
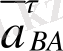 АВ кесіндісіне перпендикуляр бағытталған. Оның шамасы
АВ кесіндісіне перпендикуляр бағытталған. Оның шамасы
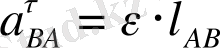
егер
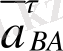 белгілі болса, онда
белгілі болса, онда
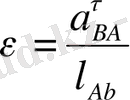
4. Екі нүкте өзара ілгерлемелі кинематикалық жұп құрай байланысқан екі звеноның бойында жатады. Нүктелер қарастырып отырған уақытта бір-біріне сәйкес келеді.
В нүктесінің жылдамдығы тасымалдау жылдамдықтары (
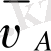 ) және салыстырмалы жылдамдықтары (
) және салыстырмалы жылдамдықтары (
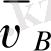 ) қосындысына тең.
) қосындысына тең.
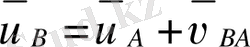
Салыстырмалы жылдамдық (
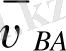 ) АХ бағыттаушысына параллель бағытталған.
) АХ бағыттаушысына параллель бағытталған.
В нүктесінің үдеуі үш үдеуден тұрады: А нүктесінің үдеуі, А нүктесіне байланысты алынған үдеу және Корнолис үдеуінен.
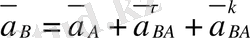
В нүктесінің жанама үдеу векторы
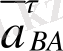 салыстырмалы жылдамдық векторы
салыстырмалы жылдамдық векторы
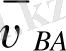 сияқты ХХ бағыттаушысына параллель бағытталған.
сияқты ХХ бағыттаушысына параллель бағытталған.
Тасымалдау (айналу) және салыстырмалы үдеулердің нәтижесінде пайда болған Королис үдеуінің шамасы
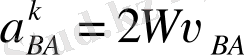
Королис үдеуінің бағытын анықтағанда оны салыстырмалы жылдамдықтың бағытымен бағыттай отырып, онан кейін бұрыштық жылдамдық бағыты бойынша 90° бұрайды.
Ассур топтарының жылдамдықтарын және үдеулерін анықтау
1. ІІ классты Ассур тобының 1-ші түрі.
Берілгені: А және С нүктелерінің жылдамдықтары
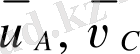
Табу керек:
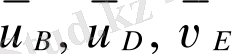 нүктелерінің жылдамдықтарын;
нүктелерінің жылдамдықтарын;
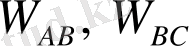 звеноларының бұрыштық жылдамдықтарын.
звеноларының бұрыштық жылдамдықтарын.
В нүктесінің жылдамдығын тасымалдау және салыстырмалы қозғалыстарының қосындысы ретінде жазамыз.
,
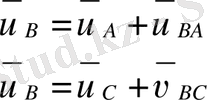
В нүктесінің жылдамдығының шамасы, бағыты бойынша белгісіз.
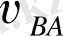 және
және
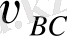 салыстырмалы жылдамдықтары шамасы бойынша белгісіз, бағыты бойынша белгілі:
салыстырмалы жылдамдықтары шамасы бойынша белгісіз, бағыты бойынша белгілі:
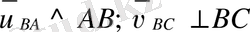
Векторлық теңдеулер жүйесі анықталған болады егер теңдеулер саны белгісіздер санын 2-ге көбейткенде тең болса. Біз қарастырып отырған еңдеу екі векторлық теңдеуден және төрт белгісізден тұрады.
Жылдамдықтар жобасын саламызи (сурет )
Өзіміз қабылдап алған [pa] кесіндісін
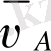 векторының бойымен саламыз.
векторының бойымен саламыз.
Жылдамдық жобасының масштабтық коэффициентін анықтаймыз:
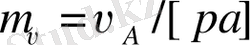
Масштабтық коэффициентті ескере отырып [pa] кесіндісін
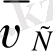 векторы бойымен саламыз
векторы бойымен саламыз
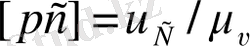
А нүктесі арқылы АВ-ға перпендикуляр түзуін жүргіземіз. С нүктесі арқылы ВС-ға перпендикуляр сызығын жүргіземіз. Осы түзулердің қиылысқан жері бізге теңдеуінің жалпы шешімін береді. Д нүктесінің жылдамдығын ұқсастықтар заңы бойынша табамыз.
Бұл үшіс bc кесіндісі бойынша АВДС ұқсас және сәйкес Δ bdc үшбұрышын саламыз. (ΔВДС ~ Δ bdc )
Полюсті с нүктесімен қоса отырып Д нүктесінің жылдамдығын табамыз:
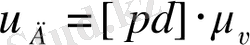
Е нүктесінің жылдамдығын да ұқсастықтар заңы бойынша табамыз:
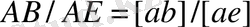
мұнан
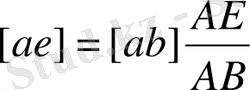
Жылдамдықтар жобасындағы [ab] кесіндісі бойнша [ae] кесіндісін өлшеп саламыз. Алынған е нүктесін полюспен қосып, Е нүктесінің жылдамдығын анықтаймыз:
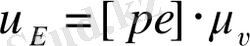
АВ және ВС звеноларының бұрыштық жылдамдықтарын анықтаймыз.
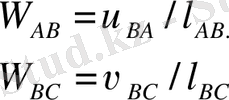
Бұрыштық жылдамдықтардың бағыттарын анықтау үшін
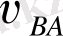 және
және
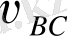 салыстырмалы жылдамдықтар векторларын ойша механизмдер жобасының В нүктесіне көшіреміз. АВ звеносын сағат тілі бойынша айналдырады, ал
салыстырмалы жылдамдықтар векторларын ойша механизмдер жобасының В нүктесіне көшіреміз. АВ звеносын сағат тілі бойынша айналдырады, ал
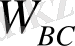 векторы ВС векторын сағат тілі бағытына кері айналады.
векторы ВС векторын сағат тілі бағытына кері айналады.
Үдеулер жобасында жылдамдықтар жобасы сияқты салынады. Салыстырмалы үдеу: нормаль және жанама үдеуге жіктеледі.
Берілгені А және С нүктелері
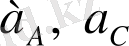 берілісін жылдамдықтар жобасы салынғандықтан барлық жылдамдықтар белгілі
берілісін жылдамдықтар жобасы салынғандықтан барлық жылдамдықтар белгілі
Табу керек:
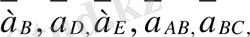 : үдеулер жобасын салу үшін векторлық теңдеу құраймыз:
: үдеулер жобасын салу үшін векторлық теңдеу құраймыз:
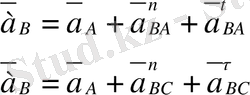
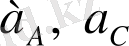 векторлары шамасы және уақыты бойынша белгілі.
векторлары шамасы және уақыты бойынша белгілі.
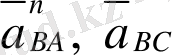 векторларының бағыттары белгілі, шамаларын келесідегі формула бойынша анықтаймыз:
векторларының бағыттары белгілі, шамаларын келесідегі формула бойынша анықтаймыз:
вектор В нүктесінен А нүктесіне қарай бағытталған
вектор В нүктесінен С нүктесіне қарай бағытталған
Жанама үдеудің бағыты ғана белгілі
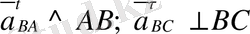 , онда төрт белгісізден тұратын екі векторлық теңдеуді пайдалана отырып В нүктесінің үдеуін табамыз.
, онда төрт белгісізден тұратын екі векторлық теңдеуді пайдалана отырып В нүктесінің үдеуін табамыз.
 кесіндісінің ұзындығын өзіміз қабылдай отырып
кесіндісінің ұзындығын өзіміз қабылдай отырып
 векторы бағыты бойынша саламыз.
векторы бағыты бойынша саламыз.
Үдеудің жобасының масштабтық коэффициентін анықтаймыз.
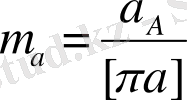
Масштабтық коэффициентін есекере отырып қалған векторларды саламыз.
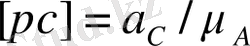
Үдеулер жобасында
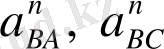 векторларын көрсететін кесінділердің шамаларын анықтаймыз.
векторларын көрсететін кесінділердің шамаларын анықтаймыз.
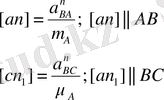
вектор В нүктесінен А нүктесіне қарай бағытталған
вектор В нүктесінен С нүктесіне қарай бағытталған
а және с нүктелерінен көрсетілген бағыт бойынша
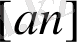 және
және
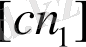 кесінділерін саламыз.
кесінділерін саламыз.
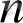 және
және
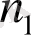 нүктелерінен жанама үдеулердің бағытқа сәйкес түзулер жүргіземіз. (
нүктелерінен жанама үдеулердің бағытқа сәйкес түзулер жүргіземіз. (
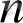 нүктесі арқылы АВ звеносына перпендикуляр,
нүктесі арқылы АВ звеносына перпендикуляр,
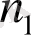 нүктесі арқылы ВС звеносына перпендикуляр)
нүктесі арқылы ВС звеносына перпендикуляр)
Осы екі түзудердің қиылысқан жерінен В нүктесінің үдеуін анықтауға болады:
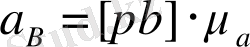
Д және Е нүктелерінің үдеулері ұқсастықтар заңдылығы бойынша анықталады. Бұл үшін [
bc
] кесіндісінің бойында, толық салыстырмалы үдеуді
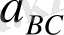 көрсететін ΔВДС ұқсас және сәкес келетін Δ
bdc
саламыз (ΔВДС ~ Δ
bdc
) .
d
нүктесін полюсқа қоса отырып Д нүктесінің үдеуін анықтаймыз:
көрсететін ΔВДС ұқсас және сәкес келетін Δ
bdc
саламыз (ΔВДС ~ Δ
bdc
) .
d
нүктесін полюсқа қоса отырып Д нүктесінің үдеуін анықтаймыз:
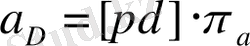
Е нүктесінде үдеуін анықтау үшін ұқсастықтар заңын пайдаланамыз:
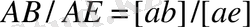 бұдан
бұдан
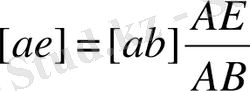
онда Е нүктесінің үдеуі
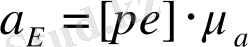
Салыстырмалы үдеудің жанама үдеулері:
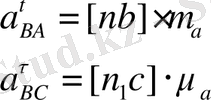
АВ және ВС звеноларының бұрыштық үдеулері:
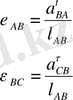
Звенолардың бұрыштық үдеулерінің бағыттарын анықтау үшін
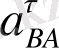 және
және
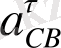 векторларының үдеулер жобасынан ойша механизм жобасының В нүктесіне көшіреміз. Бірінші вектор ВС звеносын сағат тіліне қарама-қарсы айналдырады, ал екінші вектор сағат тіліне бағыттас.
векторларының үдеулер жобасынан ойша механизм жобасының В нүктесіне көшіреміз. Бірінші вектор ВС звеносын сағат тіліне қарама-қарсы айналдырады, ал екінші вектор сағат тіліне бағыттас.
Ассур тобының 2-ші түрі
Жылдамдықтар және үдеулер жобасын салу үшін кривошипті І классқа ІІ класстыңАссур тобының 2-ші түрі қосылып алынған кривошип тиекті механизмін мысал ретінде қарастырайық.
Берілгені: Механизмнің сұлбасы, звенолардың нақты өлшемдері және кривошиптің бұрыштық жылдамдығы
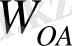 .
.
Табу керек: В нүктесінің жылдамдығын, үдеуін, АВ звеносының бұрыштық жылдамдығын және бұрыштық үдеуін.
Механизм жетекші звеноға ІІ классты жасалған Ассур тобының 2-ші түрін қосу арқылы А нүктесінің жылдамдығын табамыз:
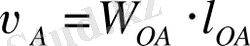
А нүктесінің жылдамдық векторы
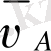 кривошип ОА-ға перпендикуляр және айналу бағытымен сәйкес бағытталған (бұрыштық жылдамдық
кривошип ОА-ға перпендикуляр және айналу бағытымен сәйкес бағытталған (бұрыштық жылдамдық
 -ға бағыты бойынша) .
-ға бағыты бойынша) .
А нүктесінің жылдамдықтар жобасында кескіндейтін [
pa
] кесінді шамасын өзіміз таңдап аламыз. Осы кесіндіні көрсетілген бағытта саламыз. Жылдамдық жобасының масштабы
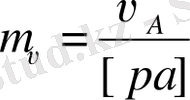
Механизмнен Ассур тобын бөліп аламыз. Ассур тобының (2, 3) В нүктесін жылдамдығын анықтау үшін векторлық теңдеу құрамыз:
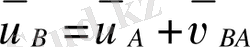 .
.
Бұл теңдеудегі
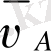 векторының шамасы, бағыты толықтай белгілі.
векторының шамасы, бағыты толықтай белгілі.
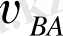 векторы АВ звеносына перпендинуляр бағытталған,
векторы АВ звеносына перпендинуляр бағытталған,
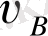 векторы ХХ өсі бойынша бағытталған.
векторы ХХ өсі бойынша бағытталған.
Векторлық теңдеу бойынша
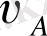 векторының алынған (а нүктесі арқылы)
векторының алынған (а нүктесі арқылы)
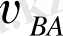 векторын жүргіземіз, онан кейін
векторын жүргіземіз, онан кейін
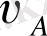 векторының басы арқылы (
р
полюс арқылы)
векторының басы арқылы (
р
полюс арқылы)
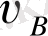 векторыг алынған бағыт бойынша жүргіземіз. Осы екі вектордың қиылысқан жері
b
нүктесін береді. Жылдамдықтар жобасынан [
ab
] және [
pb
] кесінділерін өлшеп алып
векторыг алынған бағыт бойынша жүргіземіз. Осы екі вектордың қиылысқан жері
b
нүктесін береді. Жылдамдықтар жобасынан [
ab
] және [
pb
] кесінділерін өлшеп алып
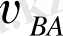 және
және
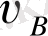 жылдамдықтарының шамасын анықтаймыз:
жылдамдықтарының шамасын анықтаймыз:
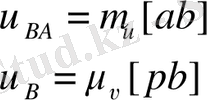
S нүктесінің жылдамдығының шамасын анықтау үшін ұқсастықтар заңдылығын пайдаланамыз:
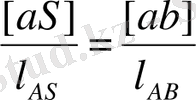
мұнан
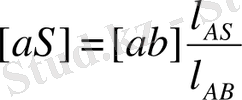
Жылдамдықтар жобасының [ ab ] кесіндісінің бойымен [ aS ] кесіндісін саламыз. Алынған S нүктесін полюспен қоса отырып [ pS ] кесіндісін аламыз. Онда S нүктесінің жылдамдығының шамасы
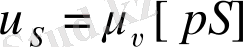
АВ звеносының бұрыштық жылдамдығы:
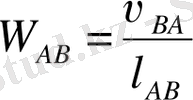
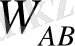 бұрыштық жылдамдықтың бағытын анықтау үшін
бұрыштық жылдамдықтың бағытын анықтау үшін
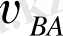 векторының механизмін В нүктесіне ойша көшіркміз. Сонан кейін осы вектормен бірге А нүктесіне байланысты қалай қозғалатынын қараймыз. Біздің жағдайда бұрыштық жылдамдық
векторының механизмін В нүктесіне ойша көшіркміз. Сонан кейін осы вектормен бірге А нүктесіне байланысты қалай қозғалатынын қараймыз. Біздің жағдайда бұрыштық жылдамдық
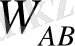 сағат тілі бағытымен бағыттас айналады. Кривошиптің бұрыштық жылдамдығы тұрақты болғандықтан А нүктесінің толық үдеуі:
сағат тілі бағытымен бағыттас айналады. Кривошиптің бұрыштық жылдамдығы тұрақты болғандықтан А нүктесінің толық үдеуі:
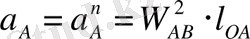
 кесіндісін өзіміз қабылдай отырып, үдеудің масштабтық коэффициентін анықтаймыз:
кесіндісін өзіміз қабылдай отырып, үдеудің масштабтық коэффициентін анықтаймыз:
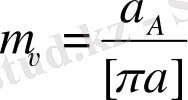
 векторы ОА кривошип бойымен, А нүктесінен О нүктесіне қарай бағытталған (кривошиптің айналу центріне қарай) .
векторы ОА кривошип бойымен, А нүктесінен О нүктесіне қарай бағытталған (кривошиптің айналу центріне қарай) .
 кесіндісін
кесіндісін
 векторы бағыты бойынша аламыз.
векторы бағыты бойынша аламыз.
Ассур тобының (2, 3) В нүктесінің жылдамдығын анықтау үшін векторлық теңдеу құрамыз:
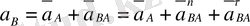
Бұл теңдеудегі
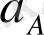 векторының шамасы, бағыты толықтай белгілі, ал
векторының шамасы, бағыты толықтай белгілі, ал
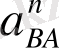 векторын кескіндейтін [
an
] кесіндісінің шамасы
векторын кескіндейтін [
an
] кесіндісінің шамасы
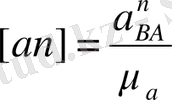
Енді векторлық теңдеудегі үдеулердің бағытын анықтаймыз:
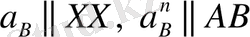 (В нүктесінен А нүктесіне қарай бағытталған),
(В нүктесінен А нүктесіне қарай бағытталған),
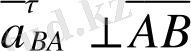 . Онда а нүктесінен
. Онда а нүктесінен
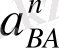 векторы бағыты бойынша [
an
] кесіндісін саламыз, ары қарай
векторы бағыты бойынша [
an
] кесіндісін саламыз, ары қарай
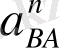 векторының соңынан (
n
нүктесі арқылы)
векторының соңынан (
n
нүктесі арқылы)
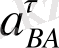 векторын саламыз. Одан кейін
векторын саламыз. Одан кейін
 полюсы арқылы
полюсы арқылы
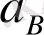 векторын саламыз. Векторлардың қиылысқан жері
b
нүктесін береді.
векторын саламыз. Векторлардың қиылысқан жері
b
нүктесін береді.
Үдеулер жобасынан
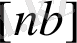 және
және
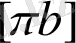 кесінділерін өлшей отырып
кесінділерін өлшей отырып
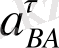 және
және
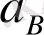 векторларының шамасын анықтаймыз:
векторларының шамасын анықтаймыз:
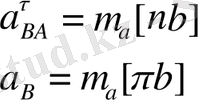 Үдеулер жобасындағы а және
b
нүктелерін қоса отырып [
ab
] кесіндісін аламыз.
Үдеулер жобасындағы а және
b
нүктелерін қоса отырып [
ab
] кесіндісін аламыз.
Толық салыстырмалы үдеудің шамасын анықтау үшін [
ab
] кесіндісін өлшеп аламыз. Онда
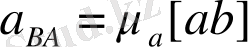 .
.
S
нүктесінің үдеуінің шамасын анықтау үшін ұқсастықтар заңдылығын пайдаланамыз:
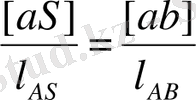
мұнан
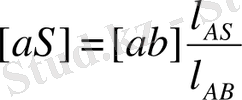
Алынған [
aS
] кесіндісін [
ab
] кесіндісінің бойына сала отырып
S
нүктесін полюспен қосамыз, онда
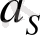 векторын үдеулер жобасында кескіндейтін
векторын үдеулер жобасында кескіндейтін
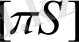 кесіндісін аламыз.
кесіндісін аламыз.
S
нүктесінің үдеуінің шамасы:
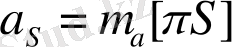
АВ звеносының бұрыштық үдеуінің шамасы
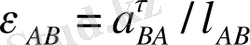
Бұрышықтың үдеудің
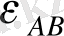 бағытын анықтау үшін
бағытын анықтау үшін
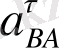 векторының механизм жобасын В нүктесіне ойша көшіреміз, сонан кейін осы вектормен бірге А нүктесіне байланысты қалай қозғалатынын қараймыз.
векторының механизм жобасын В нүктесіне ойша көшіреміз, сонан кейін осы вектормен бірге А нүктесіне байланысты қалай қозғалатынын қараймыз.
Біздің жағдайда бұрыштық үдеу
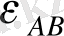 бағыты сағат тілімен бағыттас.
бағыты сағат тілімен бағыттас.
Ассур тобының 3-ші түрі
Жылдамдықтар және үдеулер жобасын салу үшін І классқа ІІ классты Ассур тобының 3-ші түрі қосылып алынған кулисалы механизм мысал ретінде қарастырайық.
Берілгені: Механизмнің сұлбасы, звенолардың нақты өлшемдері және кривошиптің бұрыштық жылдамдығы.
Табу керек: Кулисаның В және Д нүктелерінің жылдамдығын, үдеуін. Кулисаның бұрыштық жылдамдығын және бұрыштық үдеуін.
А нүктесінің жылдамдығының шамасы
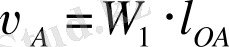
Жылдамдықтар жобасын салу үшін векторлық теңдеу құраймыз:
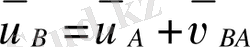 (В нүктесі 3-ші звеноға жатады және механизмнің қарасытырып отырған жағдайда 1-ші звеноның А нүктесімен сәйкес келеді) .
(В нүктесі 3-ші звеноға жатады және механизмнің қарасытырып отырған жағдайда 1-ші звеноның А нүктесімен сәйкес келеді) .
Бұл векторлық теңдеуге
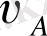 векторы шамасы бойынша толықтай белгілі, ал
векторы шамасы бойынша толықтай белгілі, ал
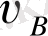 және
және
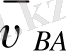 векторларының бағыттары ғана белгілі.
векторларының бағыттары ғана белгілі.
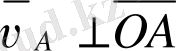 (бағыты 1-ші звеноның айналу жылдамдығының бағыты бойынша алынады),
(бағыты 1-ші звеноның айналу жылдамдығының бағыты бойынша алынады),
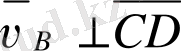 ,
,
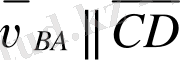
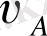 векторын жылдамдықтар жобасында кескіндейтін [
pa
] кесіндісіз өзіміз таңдап аламыз.
векторын жылдамдықтар жобасында кескіндейтін [
pa
] кесіндісіз өзіміз таңдап аламыз.
Онда жылдамдықтың масштабтық коэффициенті
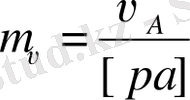
Жылдамдықтардың векторлық теңдеуіне сәйкес
p
полюсынан
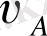 векторының бағыты бойынша [
pa
] кесіндісін саламыз. а нүктесі арқылы
векторының бағыты бойынша [
pa
] кесіндісін саламыз. а нүктесі арқылы
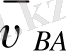 векторын бағытын жүргіземіз. (
векторын бағытын жүргіземіз. (
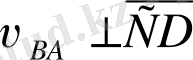 ) сонан кейін полюс арқылы
) сонан кейін полюс арқылы
 векторы бағытын жүргіземіз (
векторы бағытын жүргіземіз (
 ) .
) .
Векторлардың қиылысқан жерін (
b
нүктесі) бойынша [
ab
] және [
pb
] кесінділерін өлшеп алып
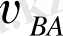 және
және
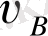 вектордларының шамасын анықтаймыз:
вектордларының шамасын анықтаймыз:
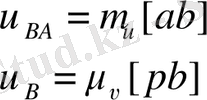
Д нүктесінің жылдамдығының ұқсастықтар заңдылығы бойынша анықтаймыз. С, В және Д нүктелері бір түзудің және 3-ші звеноның бойыеда жатыр. Сондықтан с, b және d нүктелері жылдамдықтар жобасында бір түзудің бойында жату керек. Ұқсастыұтар заңдылығы бойынша
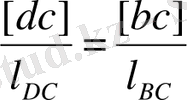
мұнан
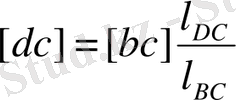 (С нүктесінің жылдамдығы нөльге тең болғандықтан жылдамдықтар жобасында ол полюсте жатады) .
(С нүктесінің жылдамдығы нөльге тең болғандықтан жылдамдықтар жобасында ол полюсте жатады) .
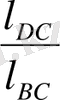 нақты өлшемдердің орнына механизмдер жобасынан
нақты өлшемдердің орнына механизмдер жобасынан
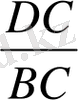 масштабтық өлшемін алуға болады. (өйткені
масштабтық өлшемін алуға болады. (өйткені
 айнамалы болғандықтан берілмеген)
айнамалы болғандықтан берілмеген)
Онда механизмдер жобасынан ДС және ВС өлшем аламыз да, [
dc
] кесіндісінің шамасын анықтаймыз:
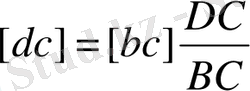
[
dc
] кесіндісінің полюстан бастап немесе С нүктесінен [
cb
] кесіндісінің бойына сала отырып (олар бір нүктеде жатады)
d
нүктесін аламыз. Жылдамдықтар жобасынан
 векторын кескіндейтін [
pd
] кесіндісін өлшеп алып,
векторын кескіндейтін [
pd
] кесіндісін өлшеп алып,
 векторының шамасын анықтаймыз:
векторының шамасын анықтаймыз:
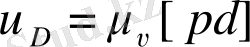
Кулисаның бұрыштық жылдамдығы:
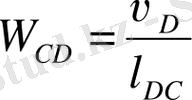
Бұрыштық жылдамдықтың бағытын анықтау үшін
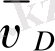 векторын ойша механизмнің Д нүктесіне көшіреміз. Біздің жағдайда
векторын ойша механизмнің Д нүктесіне көшіреміз. Біздің жағдайда
 сағат тілі бағытына қарама-қарсы бағытталған.
сағат тілі бағытына қарама-қарсы бағытталған.
А нүктесінің үдеуінің шамасы:
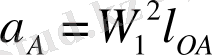
Үдеулер жобасын салу үшін векторлық теңдеу құрасыз:
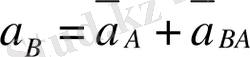
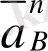 векторын жіктесек:
векторын жіктесек:
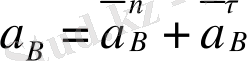 (В нүктесі центрі С нүктесінде болатын радиусы
(В нүктесі центрі С нүктесінде болатын радиусы
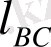 -ға тең шеңбер доғасы бойымен қозғалады) .
-ға тең шеңбер доғасы бойымен қозғалады) .
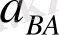 векторын
векторын
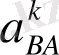 королис үдеуі және
королис үдеуі және
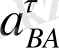 жанама үдеуіне жіктейміз:
жанама үдеуіне жіктейміз:
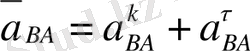 . Онда үдеулер жобасын салу үшін векторлық теңдеу келесідей түрде жазылады:
. Онда үдеулер жобасын салу үшін векторлық теңдеу келесідей түрде жазылады:
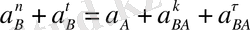 мұндағы
мұндағы
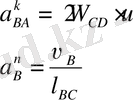 (мұндағы
(мұндағы
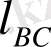 өзгеріп отыратын қашықтықтың нақты шамасын, механизмнің жобасынан анықтаймыз:
өзгеріп отыратын қашықтықтың нақты шамасын, механизмнің жобасынан анықтаймыз:
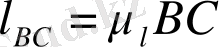 )
)
Енді векторлардың бағыттарына келсек:
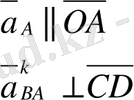
(А нүктесінен О нүктесіне қарай бағытталған)
(
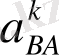 векторының бағытын аныұтау үшін ДС бағыттаушысы бойымен төмен бағытталған
векторының бағытын аныұтау үшін ДС бағыттаушысы бойымен төмен бағытталған
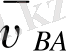 векторын
векторын
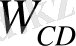 бағыты бойынша 90° бұрамыз)
бағыты бойынша 90° бұрамыз)
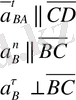
(В нүктесінен С нүктесіне қарай бағытталған)
 кесіндісін қабылдай отырып үдеудің масштабтық коэффицентін анықтаймыз:
кесіндісін қабылдай отырып үдеудің масштабтық коэффицентін анықтаймыз:
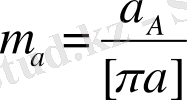 онда
онда
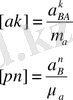
Үдеулер жобасының векторлық теңдеуінің оң жағына сәйкес үдеу векторларының көрсетілген бағыттары бойынша
 және [
ak
] кесіндлердің ретімен саламыз. К нүктесі арқылы
және [
ak
] кесіндлердің ретімен саламыз. К нүктесі арқылы
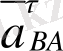 векторының ағытын жүргіземіз. Теңдеудің сол жағына сәйкес поюстан
векторының ағытын жүргіземіз. Теңдеудің сол жағына сәйкес поюстан
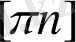 кесіндісін саламыз және
n
нүктесі арқылы
кесіндісін саламыз және
n
нүктесі арқылы
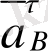 векторының бағытын жүргіземіз.
векторының бағытын жүргіземіз.
Осы векторлардың қиылысқан жері ( b нүктесінде) [ kb ] және [ nb ] кесінділерінің шамасын береді.
В нүктесін полюспен қоса отырып
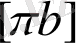 кесіндісін аламыз. Онда
кесіндісін аламыз. Онда
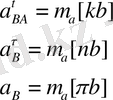
Ұқсастықтар заңдылығы бойынша Д нүктесінің үдеуінің шамасын табамыз:
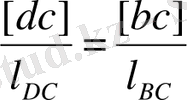 мұнан
мұнан
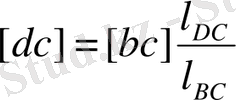 (
(
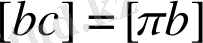 өйткені С нүктесінің үдеуі нөльге тең болғандықтан ол полюста жатады) .
өйткені С нүктесінің үдеуі нөльге тең болғандықтан ол полюста жатады) .
[ dc ] кесіндісін полюстан [ bc ] кесіндісі бойымен сала отырып d нүктесін аламыз. c, b және d нүктелері үдеулер жобасында бір түзудің бойында жатады, өйткені звеноларға сәкес С, В, Д нүктелері де бір түзудің бойында жатады.
Үдеулер жобасындағы
 векторын кескіндейтін
векторын кескіндейтін
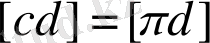 кесіндісін өлшей отырып
кесіндісін өлшей отырып
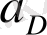 векторының шамасын анықтаймыз:
векторының шамасын анықтаймыз:
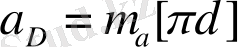
Жылдамдықтар және үдеулер аналогі
Көптеген жағдайларда және механизмдерді жобалағанда звеноның уақыт функциясындағы қозғалыс заңы заңы механизмге түсірілген күштерді ескере отырып динамикалық талдау жасағаннан кейін ғана анықтауға болады. Бұл жағдайларда звеноның қозғалысы екі этоп бойынша анықталады:
1) Кинематикалық параметрлердің жалпылама координаталар функциясындағы тәуелділіктері анықталады.
2) Жалпылама координаталардың уақыт бойынша өзгеру заңдылығы.
Мұндай есептеулерді жүзеге асыру үшін жылдамдықтар және үдеулер аналогтары деген түсінік еңгізіледі.
Құрылымдық сұлбасы және звенолардың өлшемдері берілген бір-біріне тәуелсіз механизмдердің кинематикалық параметрлер саны механизмнің қозғалыс дәрежелер санына немесе механизмгің жалпылама координаталар санына тең.
Мысалы: Тірекпен айналмалы жұп құрай отырып тірек бойымен айналмалы қозғалыс жасайтын звеноның қозғалыс дәрежесі бірге тең және оның орны бір параметрмен анықталады. (
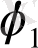 бұрыштық координатасы бойынша)
бұрыштық координатасы бойынша)
Тірекке байланысты ілгерлемелі қозғалыс жасайтын звеноның қозғалыс дәрежесіде бірге тең және оның орны бір параметр арқылы анықталады (
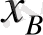 координатасы бойынша) . Сол сияқты тірекпен сфералық кинематикалық жұп құрай отырып, тірек бойымен айналмалы қозғалыс жасайтын звеноның қозғалыс дәреже саны үшке тең және оның орны үш параметрмен анықталады (
координатасы бойынша) . Сол сияқты тірекпен сфералық кинематикалық жұп құрай отырып, тірек бойымен айналмалы қозғалыс жасайтын звеноның қозғалыс дәреже саны үшке тең және оның орны үш параметрмен анықталады (
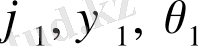 Эйлер бұрыштары бойынша)
Эйлер бұрыштары бойынша)
Қарастырып отырған санақ жүйесі басынан қозғалатын нүкте дейінгі өзгермейтін қашықтықтың нүктенің радиус-векторы деп аталады.
... жалғасы- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz