Еркін векторлар: анықтамалар, сызықтық амалдар, тәуелділік және координаталық өрнектеу


1 Лекция. Еркін векторлардың әртүрлі анықтамалары. Еркін векторларға қолданылатын сызықтық амалдар және олардың қасиеттері. Векторлардың сызықтық тәуелдігі және тәуелсіздігі, векторлардың сызықтық тәуелділігінің геометриялық мағынасы.
Анықтама: Бағытталған кесінді (немесе реттелген қос нүкте) вектор деп аталады.
А
 В
В
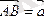

А нүктесі вектордың бастапқы нүктесі (басы), ал В-соңғы нүктесі (ұшы) деп аталады. Векторды былай белгілейді:
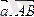 .
.
Анықтама: Вектордың бастапқы және соңғы нүктелері беттесіп кетсе, оны нолдік вектор деп атайды. Нолдік векторды былай белгілейді:
 . Нөл векторлардың бағыттары анықталмаған, модульдері нөлге тең.
. Нөл векторлардың бағыттары анықталмаған, модульдері нөлге тең.
Анықтама:Вектордың басы мен ұшының ара қашықтығы оның ұзындығы немесе модулі деп аталады. Былай белгіленеді:
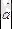 немесе
немесе
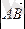 .
.
Анықтама: Модульдері бірге тең векторлар бірлік немесе орт вектор деп аталады. Берілген
 векторының орт векторы
векторының орт векторы
 деп белгіленеді және оның бағыты
деп белгіленеді және оның бағыты
 векторының бағытымен бір бағыттас болады.
векторының бағытымен бір бағыттас болады.
Анықтама: Бір түзудің немесе параллель түзулердің бойында жатқан векторлар коллинеар деп аталады.

 А В С
А В С






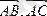 - коллинеар векторлар.
- коллинеар векторлар.
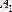
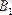

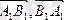 - коллинеар векторлар.
- коллинеар векторлар.



Анықтама: Өзара коллинеар, ұзындықтары тең және бағыттары бірдей векторлар тең векторлар деп аталады.
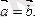
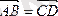 деп белгіленеді.
деп белгіленеді.
Векторларға қолданылатын сызықтық амалдар.
Анықтама:
 векторын нақты λ санына көбейту деп мына шарттарды қанағаттандыратын
векторын нақты λ санына көбейту деп мына шарттарды қанағаттандыратын
 векторын айтады:
векторын айтады:
1.
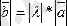
2.
 вектор
вектор
 векторына коллинеар.
векторына коллинеар.
3.
 және
және
 векторының бағыттары бірдей, егер
векторының бағыттары бірдей, егер
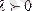 және қарама-қарсы бағытталған, егер
және қарама-қарсы бағытталған, егер
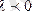 . Егерде
. Егерде
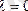 болса, онда векторлардың бағыттары анықталмаған, яғни кез келген бағытты қабылдайды.
болса, онда векторлардың бағыттары анықталмаған, яғни кез келген бағытты қабылдайды.

-
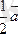

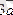
1-қасиеті.
Кез келген α және β сандары және
 векторы үшін мына теңдік орынды:
векторы үшін мына теңдік орынды:
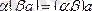 .
.
2-қасиеті.
Екі вектордың қосындысында ауыстырымдылық заңы орындалады, яғни кез келген екі вектор

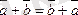
3-қасиеті.
Үш вектордың қосындысына терімділік заңы орындалады, яғни әруақытта
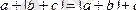
4-қасиеті.
Векторлардың қосындысын санға көбейту үлестірімді, яғни кез келген
 ,
,
 векторлары мен α саны үшін мына теңдік орындалады:
векторлары мен α саны үшін мына теңдік орындалады:
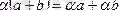
5-қасиеті.
Кез келген α, β сандары және кез келген
 векторы үшін
векторы үшін
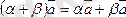 теңдігі орындалады. Екі бөлігіндегі векторлар өзара коллинеар.
теңдігі орындалады. Екі бөлігіндегі векторлар өзара коллинеар.
Анықтама: Параллель көшіруге болатын векторларды бос векторлар дейді, яғни бастапқы нүктесіне тәуелсіз, тек
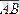 векторының ұзындығы мен бағытына ғана тәуелді вектор.
векторының ұзындығы мен бағытына ғана тәуелді вектор.

А В А
 В
В

 векторларын қарастырамыз. Бұл векторлардың қосындысы
векторларын қарастырамыз. Бұл векторлардың қосындысы
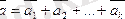 басы бірінші вектордың басымен беттесетін, ал ұшы соңғы вектордың ұшымен сәйкес келетін бір вектормен анықталады.
басы бірінші вектордың басымен беттесетін, ал ұшы соңғы вектордың ұшымен сәйкес келетін бір вектормен анықталады.
Векторларды азайтуды екі вектордың қосындысы түрінде қарастыруға болады, тек екінші қосылғыш (-) таңбасымен алынады.
Теорема:
 және
және
 векторларын
векторларын
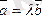 (1)
түрінде өрнектесе, онда бұл векторлар коллинеар және керісінше, егер екі вектор коллинеар болса, онда оларды
(1)
қатыс түрінде өрнектеуге болады.
(1)
түрінде өрнектесе, онда бұл векторлар коллинеар және керісінше, егер екі вектор коллинеар болса, онда оларды
(1)
қатыс түрінде өрнектеуге болады.
Анықтама: Векторлардың е осіне проекциясы дегеніміз бас нүктесі вектордың оське түсірілген бас нүктесінің проекциясы болатын, ал соңғы нүктесі вектордың ұшының оське түсірілген проекциясы болатын кесіндінің ұзындығы және ол вектор мен ось арасындағы бұрыш сүйір болса оң (+) таңбамен, ал доғал болса теріс (-) таңбамен алынады.

Мысал. Ұзындығы
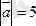 тең
тең
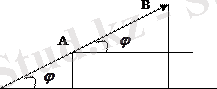
 векторы ох осімен 60
векторы ох осімен 60
 бұрыш жасайды. Осы вектордың ох осіндегі проекциясын табу керек.
бұрыш жасайды. Осы вектордың ох осіндегі проекциясын табу керек.
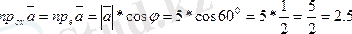
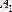
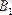 е
е
Векторлардың қосындыларының проекциясы әр вектордың проекцияларының қосындысына тең:
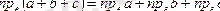
1.
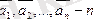 векторлары берілсін делік. Осы n векторлардың біреуін қалғандарының сызықтық комбинациясы түрінде өрнектеуге мүмкін болса, онда оларды сызықты тәуелді деп атайды.
векторлары берілсін делік. Осы n векторлардың біреуін қалғандарының сызықтық комбинациясы түрінде өрнектеуге мүмкін болса, онда оларды сызықты тәуелді деп атайды.
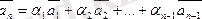
2.
Егер
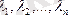
 сандары табылып берілген
сандары табылып берілген
 n векторымен
n векторымен
 түрінде өрнектеуге мүмкін болса, онда векторлар сызықты тәуелді деп аталады.
түрінде өрнектеуге мүмкін болса, онда векторлар сызықты тәуелді деп аталады.
Векторларды жіктеу.
1-теорема:
Кез келген жазықтықтағы
 векторын коллинеар емес екі векторға жіктеуге болады:
векторын коллинеар емес екі векторға жіктеуге болады:
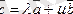
2-теорема:
Кез келген кеңістіктегі
 векторын коллинеар емес үш векторға жіктеуге болады:
векторын коллинеар емес үш векторға жіктеуге болады:
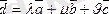
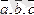 коллинеар емес векторлар.
коллинеар емес векторлар.
Тік бұрышты декарттық координаталар жүйесі.
Координаталар жүйесін былай енгіземіз: өзара перпендикуляр бірлік
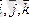 векторларын аламыз да оларды созып, x, y, z координаталық осьтерін саламыз және өлшем бірлігін енгіземіз.
векторларын аламыз да оларды созып, x, y, z координаталық осьтерін саламыз және өлшем бірлігін енгіземіз.
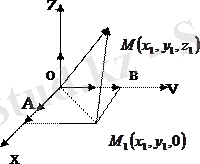
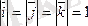

Анықтама:
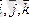 үштік векторы соңғы вектордың ұшынан қарағанда І-ші вектордан екіншіге қысқаша бұру сағат тілі жүрісіне қарсы бағытталса оң деп аталады. ОММ
үштік векторы соңғы вектордың ұшынан қарағанда І-ші вектордан екіншіге қысқаша бұру сағат тілі жүрісіне қарсы бағытталса оң деп аталады. ОММ
 үшбұрышынан
үшбұрышынан
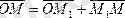
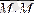 векторы
векторы
 бірлік векторына коллинеар болғандықтан
бірлік векторына коллинеар болғандықтан
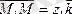
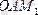 үшбұрышынан
үшбұрышынан
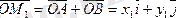
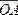 және
және
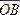 векторлары
векторлары
 және
және
 векторларына коллинеар. Өйткені осы табылған мәндерді орындарына қоямыз.
векторларына коллинеар. Өйткені осы табылған мәндерді орындарына қоямыз.
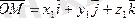 (2)
(2)
Сонымен
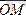 радиус-векторы М нүктесінің координаталарының
радиус-векторы М нүктесінің координаталарының
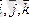 бірлік векторларына көбейтінділерінің қосындысы түрінде өрнектеледі.
бірлік векторларына көбейтінділерінің қосындысы түрінде өрнектеледі.
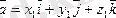 және
және
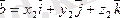 екі векторды аламызда оларды қосамыз
екі векторды аламызда оларды қосамыз
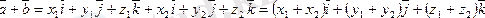
Векторларды қосқанда олардың аттас координаталары қосылады.
 векторын λ санына көбейтеміз:
векторын λ санына көбейтеміз:
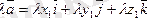 Векторды λ санына көбейткенде оның әрбір координатасы сол санға көбейтіледі.
Векторды λ санына көбейткенде оның әрбір координатасы сол санға көбейтіледі.
Ескерту: (2) қатыс вектордың векторлық түрі болып табылады, ал координаталық түрі мына түрде беріледі:
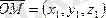 (2')
(2')
Мысал:
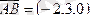 және
және
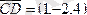 векторлары берілген. Табу керек:
векторлары берілген. Табу керек:
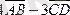 ізделінді векторды векторлық түрде береміз:
ізделінді векторды векторлық түрде береміз:
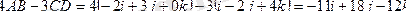 координаталық түрде
координаталық түрде
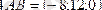

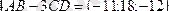
1-есеп:
Кеңістікте
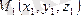 және
және
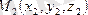 нүктелері берілген.
нүктелері берілген.
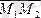 векторларын табу керек.
векторларын табу керек.
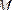
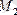
 Радиус векторды табамыз:
Радиус векторды табамыз:
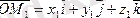
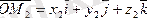
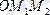 үшбұрышынан
үшбұрышынан

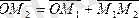
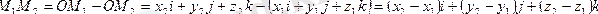 векторлық түрде:
векторлық түрде:
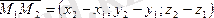 .
(2'')
.
(2'')
Вектордың координаталарын табу үшін вектор ұшының координаталарынан вектор басының сәйкес координаталарын алу қажет.
Мысал:
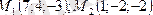
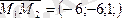
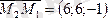 .
.
2-есеп:
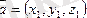 векторының ұзындығын табу керек
векторының ұзындығын табу керек
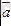 ?
?
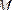
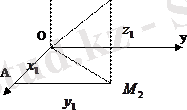
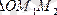 : - гипотенузасын табамыз:
: - гипотенузасын табамыз:
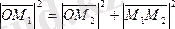
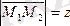
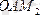 :
:
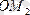 табамыз:
табамыз:
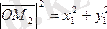
Сонда
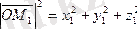
Сонымен, вектордың ұзындығы мына формуламен табылады.
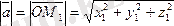
... жалғасы
- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz