Алгебрадағы теңсіздіктерді дәлелдеу әдістері және олимпиадалық қолданылуы


Мазмұны
Кіріспе . . . 3
1. Алгебрада теңсіздіктерді дәлелдеу әдістері
1. «Теңсіздіктерді дәлелдеу» тақырыбын оқытудағы жаңа технологиялар . . . 5
1. 2 Теңсіздіктерді дәлелдеу . . . 11
2. Теңсіздіктерді дәлелдеу әдістері
2. 1 Қарапайым теңсіздіктерді Штурм әдісін қолданып дәлелдеу . . . 15
2. 2 Арифметикалық, геометриялық, квадраттық, гармониялық орталардың ара қатынасын қолдану әдісі . . . 16
2. 3 Коши-Буняковский әдісін қолдану . . . 17
2. 4 Жаңа айнымалы енгізу әдісі . . . 18
2. 5 Математикалық индукция тәсілін қолдану . . . 19
2. 6 Туынды мен интегралды қолданып дәлелдеу тәсілі . . . 20
3. Олимпиадада теңсіздіктерді шешу және дәлелдеу әдістері
3. 1 Мектепішілік олимпиада . . . 21
3. 2 Аудандық олимпиада . . . 22
3. 3 Облыстық олимпиада . . . 23
3. 4 Республикалық олимпиада . . . 24
3. 5 Халықаралық олимпиада . . . 25
Қорытынды . . . 27
Пайдаланылған әдебиеттер . . . 28
Кіріспе
Қазіргі кезде ғылым мен техниканың даму деңгейі әрбір адамды сапалы және терең білім мен іскерліктің болуын, ойлау қабілетінің жоғары, шығармашылықпен жұмыс істеуін талап етеді. Оқушылардың математика-лық білімін жоғары деңгейде оқыту, яғни тереңдету әр ұстаздың алдындағы міндет.
Мұғалім шеберлігінің негізгі көрсеткіштерінің бірі-әдістеме саласындағы ғылыми жаңалықтар мен озық тәжірибені жетік игеру.
Оқушылардың білімділік және тәрбиелік деңгейі шешуші дәрежеде мұға-лімге байланысты, яғни мұғалім ізденісін қажет етеді. Дарынды балалардың қабілетін дамытудың жолдары көп. Соның ішінде олимпиадалардың ролі ерекше. Оқушылардың пәнге қызығушылығын оятатын, олардың математи-калық ой-өрісінің, шығармашылық қабілетінің дамуына дәнекер болатын қосымша тақырыптар көп әсерін тигізеді. Атап айтқанда, «Математикалық индукция әдісі», «Диофант теңдеулері», «Параметрлі теңдеулер мен теңсіз-діктер», «Комбинаторика», «Тригонометриялық өрнектерді түрлендіру», «Теңсіздіктерді дәлелдеу» және тағы да басқа тақырыптарды айтуға болады. Бұндай тақырыптар математикалық пән олимпиадаларында өз үлесін қосары сөзсіз.
Олимпиадаға дайындалу кезінде әрбір тараудың есептерін шешудің бірне-ше тәсілдерін қарастырамыз. Олимпиадалық есептерді алып қарайтын болсақ, қиындығы өте жоғары. Мұндай есептерді шығару оқушылардан терең ізденуді, терең ойлануды, еңбекқорлықты, шыдамдылықты талап етеді және соған тәрбиелейді. Олимпиадада кездесетін есептер мектеп көлемінде нақты оқылмайды, сондықтан оған қосымша ізденіп, еңбектену керек.
Қарастырғалы отырған тақырыптар: «Теңсіздіктерді дәлелдеу» және «Математикалық индукция әдісі» . Теңсіздіктерді дәлелдеу кезінде матема-тикалық индукция әдісін қолдануға болады. Математикалық индукция әдісін пайдаланып натурал сан немесе натурал санға байланысты ұғымдары бар математикалық негіздеуді қажет ететін сөйлемдер дәлелденеді. Теңбе-теңдік-терді дәлелдеуге, шектеулі қосындыларды есептеуге және теңсіздіктерді шешуге көптеген дәлелдеу жолымен көз жеткізуге болады. Математикалық индукция әдісіне және теңсіздіктерді дәлелдеу тақырыптарына қысқаша ғана тоқталып, мектепаралық, аудандық, облыстық, республикалық, халықаралық олимпиадаларда осы тақырыптар бойынша шығарылған қиын есептерге тоқталмақпын.
1. Алгебрада теңсіздіктерді дәлелдеу әдістері
1. «Теңсіздіктерді дәлелдеу» тақырыбын оқытудағы жаңа технологиялар
Қазақстан республикасындағы бүгінгі күнде орта мектептердің алдына қойылып отырған мақсаттардың бірі өркениетті елдің ұрпағын тәрбиелеп шығару. Бұл мақсат әрбір орта мектептің математика пәні мұғалімдерінің бүгінгі заман талабына сай оқыту әдістемесін күннен - күнге жетілдіре түсуін талап етеді. Талаптың орындалуы студенттерді кәсіби біліктілікке университет қабырғасында баулып, болашақтағы мамандықтарына қаншалықты даярланғандығына да байланысты. Олай болса, талап деңгейінен шығудың бір тәсілі - студенттердің сабаққа деген қызығушылықтарын оятып, оларды университет қабырғасында зерттеу жұмыстарына баулып, ой қозғату. Ол үшін жоғары оқу орындарында оқытудың жаңа технологиялардың бірі - оқытуды интербелсенді ұйымдастыру керек. Өйткені, интербелсенді оқытудағы ерекшелік - сабақтың оқу мақсаты студенттер мұқтаждары мен мүдделеріне сәйкес келетіндей және оны олардың сезініп, қызығып қабылдайтындай етіліп ұйымдастырылуында.
Жоғары оқу орындарында «Математика пәнін оқытудың теориясы мен әдістемесі» курсын оқытуда білім берудің басты тұлғасы оқытушы мен оқулық емес, керісінше, студент пен оның көзқарасы деген қағиданы негізге алатын болсақ, оқытушы үшін әр студенттің мәселені түсінудегі жүргізген зерттеулері мен өзіндік ой - толғамы, мәселеге деген көзқарасы өзінше құнды (1) .
Олай болса, Абай атындағы Қазақтың ұлттық педагогикалық университетінде «Математика пәнін оқытудың теориясы мен әдістемесі» курсын оқытуда «Теңсіздіктерді дәлелдеу» тақырыбын оқып үйретуге баулу маңызды мәселелердің бірі болып табылады. Сондықтан оқытудың жаңа технологиясын қолданып аталған тақырыпты студенттерге зерттеу тапсырмасы ретінде тапсырдық. Оқытудың әдістерін талдап келтіру үшін осы тақырыпты студенттерге зерттеу тапсырмасы ретінде тапсырғанда, студенттер зерттеу жұмыстарын жүргізу барысында мектеп оқушыларына тақырыпты оқытудың теңдіктерді дәлелдеудің негізгі әдістері төмендегі төрт мәселеге қатысты екендігін анықтады:
- анықтамаға сүйене теңсіздікті дәлелдеу,
- синтетикалық тәсіл арқылы теңсіздікті дәлелдеу,
- қарсы жору арқылы теңсіздікті дәлелдеу,
- математикалық индукция әдісі арқылы дәлелдеу.
Теңсіздіктерді дәлелдеудің төмендегідей, яғни анықтама бойынша, синтетикалық, қарсы жорып дәлелдеу, математикалық индукция әдісін қолдану сияқты түрлері бар. Теңсіздіктерді дәлелдеуде айнымалылардың мәндер жиыны көрсетілмесе, онда айнымалы кез келген нақты мәнді қабылдайды деп түсінуіміз керек. Студенттер тақырыпты оқытудың бірінші әдісі анықтамаға сүйене теңсіздікті дәлелдеу үшін анықтама бойынша,
 болу үшін,
болу үшін,
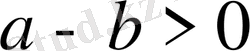 болуы керектігін, және осы тәсілмен дәлелдеу үшін
болуы керектігін, және осы тәсілмен дәлелдеу үшін
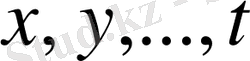 айнымалыларының берілген мәндер жиыны
айнымалыларының берілген мәндер жиыны
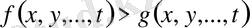 болуы қажеттігін анықтап,
болуы қажеттігін анықтап,
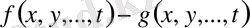 айырмасының
айырмасының
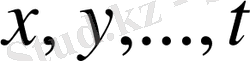 айнымалыларының берілген мәндер жиынында оң екендігін дәлелдеулері керектігіне тоқталды. Бұған аналогиялық түрде
айнымалыларының берілген мәндер жиынында оң екендігін дәлелдеулері керектігіне тоқталды. Бұған аналогиялық түрде
 теңсіздіктері де дәлелденетініне көз жеткізді. Аталған әдіске төмендегідей мысалдар келтірді:
теңсіздіктері де дәлелденетініне көз жеткізді. Аталған әдіске төмендегідей мысалдар келтірді:
1 Мысал.
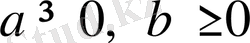 болғанда
болғанда
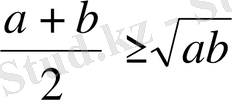 болатындығының дәлелдеуі.
болатындығының дәлелдеуі.
Дәлелдеуі.
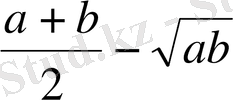 айырмасын құрамыз да, таңбасын анықтаймыз.
айырмасын құрамыз да, таңбасын анықтаймыз.
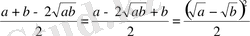 олай болса,
олай болса,
 мен
мен
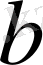 теріс емес мәндерінде бұл өрнек әрқашанда оң.
теріс емес мәндерінде бұл өрнек әрқашанда оң.
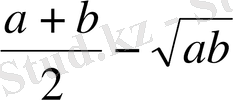 оң, яғни
оң, яғни
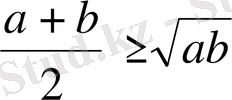 (Коши теңсіздігі) .
(Коши теңсіздігі) .
2 Мысал .
 болғанда,
болғанда,
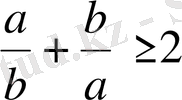 дәлелденуі.
дәлелденуі.
Дәлелдеуі.
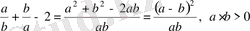 болғандықтан,
болғандықтан,
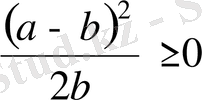 болады, ал
болады, ал
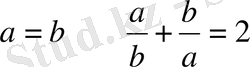 орындалады.
орындалады.
3 Мысал.
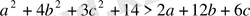 теңсіздігінің дәлелденуі.
теңсіздігінің дәлелденуі.
Дәлелдеуі.
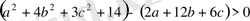
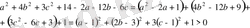
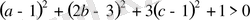 бұл өрнек
бұл өрнек
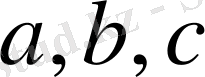 кез келген мәні үшін орындалады.
кез келген мәні үшін орындалады.
Осы сияқты студенттер екінші синтетикалық тәсіл арқылы теңсіздікті дәлелдеудің мәнін теңсіздіктерді түрлендіру нәтижесінде оларды тірек теңсіздіктеріне келтіру деп түсіндіріп, тірек теңсіздіктері:
1)
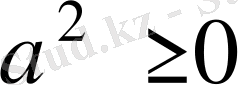 ; 2)
; 2)
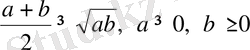 ; 3)
; 3)
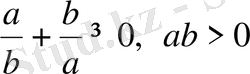 ;
;
4)
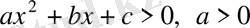 және
және
 бола алатындығына тоқталды. Оған төмендегі мысалдарды келтірді:
бола алатындығына тоқталды. Оған төмендегі мысалдарды келтірді:
1 Мысал.
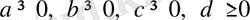 болса,
болса,
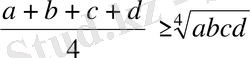 дәлелденуі.
дәлелденуі.
Дәлелдеуі. Тірек теңсіздігі ретінде Коши теңсіздігін аламыз:
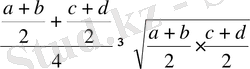 .
.
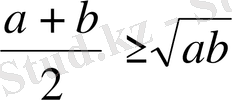 және
және
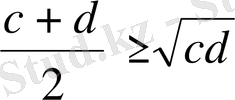 болғандықтан
болғандықтан
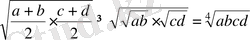 .
.
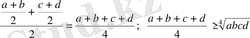 , ал
, ал
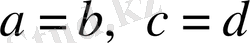 болғанда теңдік орындалады.
болғанда теңдік орындалады.
2 Мысал.
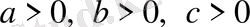 болса, онда
болса, онда
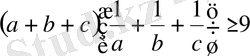 дәлелденуі.
дәлелденуі.
Дәлелдеуі. Тірек теңсіздігіне
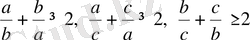 бола алады.
бола алады.
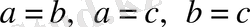 теңдік орындалады. Тірек теңсіздіктерін қосатын болсақ:
теңдік орындалады. Тірек теңсіздіктерін қосатын болсақ:
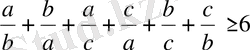 немесе
немесе
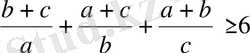 теңсіздіктің екі жағына бірдей 3-ті қосатын болсақ:
теңсіздіктің екі жағына бірдей 3-ті қосатын болсақ:
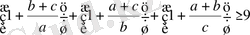
Ортақ бөлімге келтірсек:
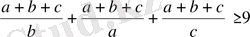
Олапй болса
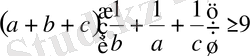 екендігі дәлелденеді.
екендігі дәлелденеді.
Студенттердің қарсы жору арқылы теңсіздікті дәлелдеу тәсілін зерттеу үшін ізденіп, келтірген мысалдарына тоқталайық:
1 Мысал.
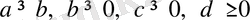 болса,
болса,
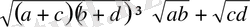 дәлелденуі.
дәлелденуі.
Дәлелдеуі. Қарсы жоримыз, яғни
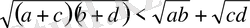 деп аламыз. Теңсіздіктің екі жағы да оң болғандықтан, квадраттаймыз:
деп аламыз. Теңсіздіктің екі жағы да оң болғандықтан, квадраттаймыз:
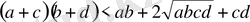
Олай болса,
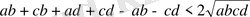 . Осыдан алынатыны:
. Осыдан алынатыны:
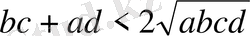
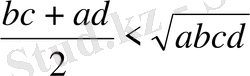 теңсіздігі Коши теңсіздігіне қарсы болғандықтан, дұрыс емес, олай болса,
теңсіздігі Коши теңсіздігіне қарсы болғандықтан, дұрыс емес, олай болса,
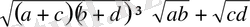 .
.
Теңсіздіктерді осы сияқты дәлелдеу үшін
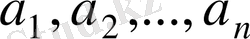 ,
,
 - теріс сан емес сандар берілсе, онда төмендегідей шамаларды енгіземіз. Олар:
- теріс сан емес сандар берілсе, онда төмендегідей шамаларды енгіземіз. Олар:
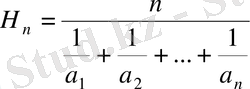 - гармониялық орта,
- гармониялық орта,
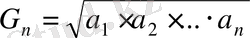 - геометриялық орта,
- геометриялық орта,
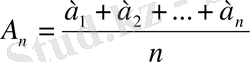 - арифметикалық орта,
- арифметикалық орта,
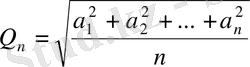 - квадраттық орта.
- квадраттық орта.
Осы орталар арасында келесі байланыстар:
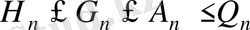 да қолданылады.
да қолданылады.
Студенттер математикалық индукция әдісін қолданып, теңсіздікті дәлелдеуге төмендегідей мысалдар келтірді.
1 Мыса.
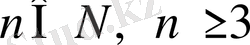 болса,
болса,
 дәлелденуі.
дәлелденуі.
Дәлелдеуі.
1)
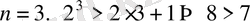 дұрыс;
дұрыс;
2)
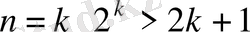 дұрыс деп санаймыз;
дұрыс деп санаймыз;
3)
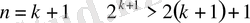 дұрыстығын дәлелдейік, яғни
дұрыстығын дәлелдейік, яғни
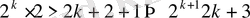
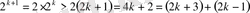
Олай болса,
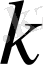 -ның кез келген мәнінде
-ның кез келген мәнінде
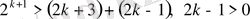 . Осылайша
. Осылайша
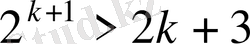 теңсіздігі дәлелденді деп есептейміз.
теңсіздігі дәлелденді деп есептейміз.
1. 2 Теңсіздіктерді дәлелдеу
Теңдуелерді зерттеу, жуық есептеу, иррационал сандар теориясы, сан қатарлары т. б. теңсіздіктер қасиетіне сүйенеді. Жоғарғы мектептегі математикалық анализ курсында функциялардың максимум және минимум яғни экстримал есептерді шешуде теңсіздіктер кең түрде қолданылады.
Тек математикада ғана емес әр түрлі жаратылыстану ғылымдарында зерттелетін табиғаттың үздіксіз процестері әсіресе экологиялық, экономикалық т. б. халық шаруашылығындағы балайланыстар теңсіздіктің көмегімен шешіледі. Теңсіздіктер оқушыларды айқын және дұрыс ойлауға, шамаларды салыстыра білуге дағдыландырады.
Әр түрлі теңсіздіктер ерте заманда-ақ белгілі болған. Эвклит пен Архимед шығармаларында көптеген теңсіздіктер келтірілген. Осы күнгі теңсіздіктер таңбасы ХVІІІ ғасырда ағылшын ғалымы Томас Гариаттың латын тілінде жазылған «Аналитикалық өнердің практикасы атты еңбегінде» тұнғыш рет келтіріледі. Теңдіктер теңсіздіктен жасалады, оларды теңсіздіктердің дербес бір түрі деуге болады. Теңсіздікті теңдікке айналдыру үшін екі шаманың айырмасын дәл бағалау керек. Теңсіздіктер жай санды теңсіздіктер, алгебралық теңсіздіктер, классикалық теңсіздіктер болып бөлінеді. Теңсіздікті дәлелдегенде және шешкенде тек әріптер мен белгісіз шамалардың мүмкін мәндерін үнемі есепке алу керек. Мысалы:таңбасы белгісіздің мүмкін мәндерінің кейбіреуінде ғана сақталатын теңсіздікті шартты немесе белгісізі бар теңсіздік деп атайды. барлық теңсіздіктердің қасиеттерін тек санды теңсіздіктер арқылы көрсетуге болады
1. а<b теңсіздігінен b>a теңсіздігі туады
2. а<b және b<c теңсіздіктерінен а<c теңсіздігі шығады
Бұл қасиет теңсіздікті шешкенде, теоремалар дәлелдегенде теңсіздікті «күшейту» үшін қолданылады.
3. а<b болса а+с<b+c болады
Теңсіздікті шешкенде, кейде ықшамдау мақсатымен оның екі бөлігінеде немесе екі бөлігінен де бірдей санды қосады немесе шегереді.
4. а-с<b болса а< b+c
Бұл қасиет бойынша теңсіздік мүшелерінең таңбасын өзгерте отырып, бір бөлігінен екінші бөлігіне көшіруге болады.
5. а<b және с<d болса а+с<b+d болады.
Шарт бойынша а-b<0 және c-d<0. Екі теріс санның қосындысы да теріс.
Теңсіздіктің дәлелдеу жолының белгілі бір алгоритмін анықтау қиын. Бірақ оған қарамастан теңсіздікті қандайда бір айқын теңсіздікке түрлендіру жолы бар екенін айта кеткен жөн. Содан кейін айқын теңсіздікті логикалық талдау арқылы берілген теңсіздікті келтіруге болады.
Негізгі теңсіздіктер: 1. а+в≥√ав, а≥0, в≥0
2. а+в≥2, (а мен в-ның таңбасы бірдей) ;
в а
3. 1:1(1+1) ≤√ав, а>0, в>0,
2 а в
Гармониялық орта;
4. 2ав≤√ав≤ а+в;
а+в 2
5. ׀а+в׀≤ ׀а׀ +׀ в׀ тек а•в≥0 болғанда орындалады
Теңсіздіктерді дәлелдеу әдістері;
1. Анықтама бойынша, яғни анықтамаға сүйеніп дәлелдеу. Мысалы,
а5-в5 ≥ а4в-ав4, мұндағы а > в
Дәлелдеу: а5-в5-а4в+ав4=а4(а-в) +в4(а-в) =(а-в) (а4+в4) ≥0
2. Дәлелденген теңсіздік көмегімен;
а>0, в>0, с>0, d>0
(1+вс) (1+cd) (1+ cd) (1+ав) ≥16
ad aв вс cd
Дәлелдеу:
Каши теңсіздігін қолданамыз
1+вс≥2√вс
ad ad
1+сd≥2√cd }→(1+вс) (1+сd) (1+ ad)
ad aв ad aв вс
(1+ав) ≥16 √вс•сd•ad•ав=16
cd ad ad вс cd
1+ad≥2√ad
вс вс
1+ав≥2√ad
сd сd
3. Талдау арқылы дәлелдеу
... жалғасы- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz