Комплекс сандарды оқытуға арналған компьютерлік бағдарламаларды құрастыру және қолдану әдістемесі


Жұмыс түрі: Дипломдық жұмыс
Тегін: Антиплагиат
Көлемі: 48 бет
Таңдаулыға:
МАЗМҰНЫ
КІРІСПЕ3
1 КОМПЛЕКС САНДАР МЕН ОЛАРҒА ҚОЛДАНЫЛАТЫН АМАЛДАР5
1. 1 Комплекс сандар ұғымы5
1. 2 Комплекс сандарға амалдар қолдану14
2. КОМПЛЕКС САНДАРДЫ ОҚЫТУҒА АРНАЛҒАН КОМПЬЮТЕРЛІК БАҒДАРЛАМА ЖАСАҚТАУ ТӘСІЛДЕРІ22
2. 1 Комплекс сандарды оқыту әдістері22
2. 2 Комплекс сандарды оқытуға арналған компьютерлік бағдарлама құрастыру29
2. 3 Компьютерлік бағдарламаны пайдалану жолдары44
ҚОРЫТЫНДЫ . . . 59
ПАЙДАЛАНҒАН ӘДЕБИЕТТЕР ТІЗІМІ61
КІРІСПЕКез -келген заманауй мамандықты игерудің бірден-бір талабының бірі математикалық біліміне сүйенеді. Заманауй әлемдегі математиканың рөлі туралы ұсыныстар жалпы мәдени ортаның қажетті қосындысы ретінде көрсетіледі. Өмірде өзін-өзі жүзеге асыру үшін, сондай-ақ ақпараттық заманында оңтайлы қызметке қол жеткізу үшін айтарлықтай берік математикалық даярлықты қажет етеді.
Сондықтан математиканы оқытудың негізгі мақсаты - заманауй қоғам мүшесінің әрқайсысының еңбек қызметіне және күнделікті өміріне қажетті, математикалық білім мен ептілік жүйесін саналы және берік игеруін қамтамасыз ету.
Білім беру жүйесінің негізгі мақсатын шешумен қатар математиканы терендетіп оқыту дегеніміз, оқушының пәнге деген тұрақты қызығушылығын қалыптастыру, олардың математикалық қабілеттерін анықтау және жетілдіру, математикамен байланысты мамандыққа бағдарлау.
Заманауй қоғамның қарқынды түрде дамуы, әртүрлі саладағы адам қызметінің жаңа ақпараттармен толықтырылуы білім жүйесіне өскелең ұрпақты оқытуда жаңа бастамаларды, сонымен қатар жаңа әдістер мен технологияларды енгізуді қажет етеді.
Қазіргі уақытта кей ғылымдарды комплекстік сандарды қолданусыз елестету қиын. Электротехника, электромеханика, радиотехника, ұшақ құру және басқа да ғылымдар теориясы комплекс сан түріндегі модельді қолданусыз мүмкін емес.
Комплекс сандарды есептеуді калькулятор немесе программалау тілдері арқылы жүргізе аламыз. Осындай программалау тілінің бірі- Соmmоn Lіsр. Соmmоn Lіsр- басқа программалау тілдеріне қарағанда математиканы жеңілдетпейді, тек оны қолдану оны қарапайым етеді.
Математиктер Lіsр-ті математикалық функцияларды зерттеу үшін құрастырған.
Қолданыстағы технологиялар мен әдістердің теориялық талдауы олардың арасынан компьтерлік оқыту бағдарламасын ең үздік технологиялық бастамалардың бірі екендігін көрсетті.
Математикалық ғылымның ерекшелігі (логикалылығы, құрылымдылығы, әмбебаптылығы) ең алдымен комплекс сандарды оқытуға арналған компьютерлік бағдарламаларға сай келеді, ол оны қолданудың мақсаттылылығын дәлелдейді.
Дипломдық жұмыстың мақсаты. Комплекс сандарды оқытуға арналған компьтерлік бағдарламаларды қолдану тәсілдері бойынша әдіснамалық ұсыныстар жасау, олар:
- қарастырылып отырған тақырып бойынша әдіснамалық ұсыныстар құрастыру;
- комплекс сандарды оқытуға арналған компьтерлік бағдарламаларды жасақтау тәсілдері.
Дипломдық жұмыстың объектісі. Комплекс сандарды оқыту әдістерін анықтау.
Дипломдық жұмыстың пәні. Комплекс сандарды оқытуға арналған компьютерлік бағдарламаларды жасақтау әдістерін зерттеу.
Дипломдық жұмыстың тәжірибелік маңыздылығы мынадан тұрады, халыққа білім беру саласындағы жаңа концепция бойынша, жаңа оқу орындарының сатылы (бакалавар, магистр) оқу жүйесіне арналған жаңа бағдарлама құрылғаны белгілі. Сондықтан да, оған сәйкестендіріліп жазылған мемлеметтік тілдегі оқулықтар мен оқу құралдарының қажеттілігі мен тапшылығы көптеген қиындықтар туғызуда. Комплекс сандарды зерттеу үшін оқу-әдіснамалық материалдар жасалынды, оларды математика пәнін тереңдетіп оқытатын мектептердің мұғалімдері қолдануы мүмкін.
Дипломдық жұмыста берілген тұжырымдардың дәлелдемелері толық қамтылған, барлық қажет жағдайларда графикалық кескіндері келтірілген.
1. КОМПЛЕКС САНДАР МЕН ОЛАРҒА ҚОЛДАНЫЛАТЫН АМАЛДАР 1. 1 Комплекс сандар ұғымыКомплекс сан ұғымы тұңғыш рет ХҮІ ғасырда итальяндықтар Дж. Кардано және Р. Бомбелли қарастырған дискриминантты теріс квадрат теңдеулердің, әсіресе кубтық теңдеулердің, шешімдеріне байланысты шыққан ұғым. 1572 жылы шыққан «Алгебра» атты кітабында Р. Бомбелли комплекс сандарға арифметикалық операциялар қолданған.
Алғашқы кезде комплекс сандардың іс жүзінде нақты түрде түсінігі (интерпретациясы), болмағандықтан ондай түбірлерді «мүмкін емес», «жорамал» деп санап, ондай түбірлері бар теңдеулерді «түбірі жоқ» теңдеулер қатарына қосатын болған.
Комплекс сандардың жан-жақты қолданылуы тек ХҮІІІ ғасырда басталды. Міне осы кезде комплекс сандардың интегралдық есептеуде механикада және геометрияда қолданулары комплекс аргументті функцияларды қарауға әкеп соқты. Осы мәселелер жайындағы зерттеулерде туған жері Швейцария болса да, отыз жылдан аса Петербург академиясында жұмыс істеп, өзін «орыс ғалымымын» деп атап өткен Леонард Эйлер (1707-1783) мен француз математигі және философы Даланбердің (1717-1783) үлесі көп.
Комплекс сандарға жазықтықтағы нүкте не вектор деп геометриялық түсінікті 1797 жылы даниялық жер өлшеуші К. Вессель (1745-1818) берген, бірақ тек атақты неміс математигі Карл Фридрих Гаусстың (1777-1855) комплекс сандарды арифметикаға, алгебраға, геометрия және математикалық анализге қолданған еңбектерінен кейін ғана көпшілік комплекс сандардың геометриялық мағынасын қолданып, оны толық пайдалана бастайды. Математикаға «комплекс сан» терминін кіргізген де, жоғарғы алгебраның негізгі теоремасының толық дәлелдеуін тұңғыш рет (1799 ) ұсынған да К. Гаусс.
Математиканың тарихи даму барысында әр қырынан қойылып, түрліше шешім тауып отырған ең басты мәселелердің бірі- сан ұғымын дамыту болды. Сан ұғымын кеңейту мәселесі алгебра ғылымының өз алдына бөлініп дербес даму жолына түсуін күрт жеделдетті, шешуі болатын теңдеулер класын көбейтті, қолданыстағы сандар теориясын байытуды, кеңейтуді талап етті.
Алгебралық теңдеулерді шешу үшін нақты сандар жеткіліксіз. Сондықтан да осы теңдеулерді шешуге деген ұмтылыс сандар ұғымының кеңеюіне әкеледі. Теңдеудің түбірін табу үшін оң сандар жеткіліксіз, сондықтан да теріс сандар және нөл енгізу қажеттілігі туындайды. [2]
Біздің дәуірімізге дейін 2 мың жыл бұрын ежелгі Египет және Вавилонда практикалық есептеулерде бөлшек сандар қолданылған. Сан ұғымы дамуының келесі кезеңі теріс сандарды енгізу-б. д. д 2 ғасыр бұрын қытай математиктері енгізген. Теріс сандар көмегімен бірыңғай жолмен шамалар өзгерісін суреттеуге болады. Б. д. д 8 ғасырда оң таңбалы санның квадраттық түбірінің екі мәні - оң және теріс бар екендігі, ал теріс таңбадан квадрат түбір шығаруға болмайтындығы белгілі болды. 16 ғасырда кубтық теңдеулерді зеттеу кезінде теріс таңбалы саннан квадраттық түбір шығару керек болды. Кубтық теңдеуді шешу формуласында кубтық және квадраттық түбір бар. Бұл формула теңдеудің бір нақты түбірі болса үзіліссіз әсер етеді, ал егер ол үш нақты түбірі болса, онда квадраттық түбірде теріс сан болады. Осы феноменді түсіндіру үшін 1545 жылы итальяндық алгебраист Дж. Кардано табиғаты жаңа санды енгізуді ұсынды. Кардано мұндай шамаларды «сандар теріс» деп атады және оларды жарамсыз деп санап, қолданбауға тырысты. Шындығында, мұндай сандардың көмегімен қандай да бір шаманың нәтижесін, осы шаманың өзгерісін көрсетуге болмайды.
Бірақ та 1572 жылы Бомбелли өз кітабында алғаш рет осы сандарға қолданылатын арифметикалық амалдар ережесін орнатты. «Жорамал сан» атауын 1637 жылы француз математигі Р. Декарт енгізді, ал 1777 жылы Х. Эйлер француз санының бірінші әріпі і қолдануды ұсынды, бұл белгіні жалпы қолданысқа К. Гаусс енгізді.
18 ғасырдың соңында француз математигі Ж. Лагранж жорамал сандар көмегімен сызықты дифференциаль теңдеулерді көрсете білді.
Я. Бернулли комплекс сандарды интегралды есептеу үшін қолданды. 18 ғасырда комплекс сан көмегімен картография, гидродинамика және т. б. байланысты қолданбалы есептер есептелінді. Бірақ та осы сандар теориясының логикалық негізі болмады.
19 ғасырда комплекс санның геометриялық талдауы алынды. Комплекс сандардың геометриялық талдауы комплекс айнымалы функциямен байланысты көптеген түсініктер табуға, олардың қолдану саласын кеңейтуге мүмкіндік берді. Комплекс сандардың көптеген сұрақтарда, жазықтықта вектормен көрсетілетін шамалары бар, керекті екендігі белгілі болды: су ағынын зерттеу кезінде, серпімділік теориясы тапсырмаларында, теориялық электротехникада. [1]
Физика және техника тапсырмалырының шешімі кері дискриминантты квадраттық теңдеулер арқылы жүргізіледі. Бұл теңдеулердің нақты сандар облысында шешімі жоқ. Бірақ мұндай көптеген тапсырмалардың шешімінің нақты физикалық мағынасы бар. Көрсетілген теңдеуді шешу нәтижесінде алынған шама мәнін комплекстік сандар деп атады. Комплекстік санды орыс авиациясының негізін қалаушы Н. Е. Жуковский қанат теориясын құру кезінде кең қолданған. Бұл теориядағы негізгі мәселелер: қанатты көтеруші күш қалай, қайдан шығатынын, оның шамасы және түсу нүктесі ұшу жағдайына қалай байланыстылығын айқындау, зерттеу. Комплекстік сандар және комплекстік айнымалылар функциясы көптеген ғылым мен техника сұрақтарында қолданыс табады.
Сан ұғымының натурал сандардан нақты сандарға дейін кеңею үрдісі тәжірибенің талаптарымен, сондай-ақ математиканың өз мұқтаждықтарымен байланысты болды. Алдымен заттарды санау үшін натурал сандар пайдаланылады.
Содан кейін:
- бөлуді орындаудың қажеттігі оң бөлшек сандар ұғымына әкеледі;
- әрі қарай, азайтуды орындау қажеттігі нөл мен теріс сандар ұғымдарына әкелді;
- ақырында оң сандардан түбір табу қажеттігі иррационал сандар ұғымына әкелді. Аталған амалдардың бәрі нақты сандар жиынында орындалады. Алайда, бұл жиында орындалмайтын операциялар да қалды, мысалы, теріс саннан квадраттық түбір табу амалы. Олай болса, сан ұғымының одан әрі кеңеюінің, нақты сандардан ерекше, жаңа сандардың пайда болуының қажеттігі бар.
Геометриялық тұрғыдан нақты сандар координаталық түзудің нүктелерімен кескінделеді. Әрбір нақты санға түзудің бір нүктесі сәйкес, ал түзудің әрбір нүктесіне бір нақты сан сәйкес келеді. Координаталық түзу түгелдей нақты сандардың бейнесімен толтырылған, яғни басқаша айтқанда «онда басқа сандарға орын жоқ». Жаңа сандардың геометриялық бейнелерін енді түзу бойында емес, координаталық жазықтықта іздеу керек деген ұйғарым туады. Бірақ координаталық ХОУ жазықтығының әрбір М нүктесін осы нүктенің координаталарымен анықтауға болады. Сондықтан жаңа комплекс сандар деген атпен жаңа ұғым енгізілді. 1545 жылы италиян оқымыстысы Дж. Кардано
(1. 1)
теңдеулер жүйесінің нақты сандар жиынында шешімі жоқ, ал оның шешімін
(1. 2)
түрінде табады. Кардано оларды «таза теріс» немесе «софистикалық теріс» шамалар деп атаған. Бірақ ол мұндай шешуді пайдасыз деп тауып, оларды қолданбауға тырысады.
Комплекс сандардың қасиетін дұрыс бағалаған ең бірінші математик Рафаэль Бомбелли (1526-1573) болды. Ол комплекс сандарды кубтық теңдеуді шешудің «келтірілмейтін» жағдайын шешуге қолданады. Ол 1572 жылы жарық көрген «Алгебра» атты еңбегінің бірінші кітабында комплекс сандарға амалдар қолданудың алғашқы ережелерін көрсетті. Бомбелли Карданоның «софистикалық теріс сандар» кездесетін барлық өрнектердің а bі түріне келетінін тағайындады. 1637 жылы француз математигі Р. Декарт «жорымал сан» терминін енгізді, ал XVІІІ ғасырдың ең атақты математиктердің бірі Л. Эйлер 1977 жылы (жорымал бірлік) санын белгілеу үшін француз сөзінің іmаgіnаіrе (жорымал) бірінші әрпін қолдануды ұсынды. 1831 жылы К. Гаусс «комплекс сан» терминин енгізді.
Жалпы комплекс сандарын интегралдық есептеуде, механикада, геометрияда қолданымдарына байланысты қалыптаса бастаған комплекс айнымалы функциялар теорясының дамуына француз математигі Даламбер, негізі швециялық болса да, өзін «орыс ғалымы» деп атап өткен Л. Эйлер көптеген үлестерін қосқан. Теорияның одан әрі дамуына неміс ғалымдары К. Гаусс, Б. Риман, француз ғалымы О. Кошилердің аттарымен қатар орыс ғалымдары Н. Е. Жуковский, М. А. Лаврентьев, М. В. Келдыштің де еңбектері зор. [4]
Анықтама.
Комплекс сандар деп
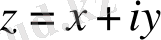
 түріндегі сандарды айтамыз, мұндағы
түріндегі сандарды айтамыз, мұндағы
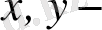 нақты сандар,
нақты сандар,
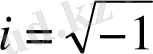 жорымал бірлік деп аталады және
жорымал бірлік деп аталады және
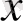 пен
пен
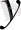 сандары
сандары
 комплекс санының сәйкес нақты және жорымал бөлігі деп аталады әрі олар
комплекс санының сәйкес нақты және жорымал бөлігі деп аталады әрі олар
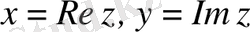 таңбаларымен белгіленеді.
таңбаларымен белгіленеді.
Сонымен, егер бізге
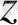 комплекс саны берілсе, онда нақты
комплекс саны берілсе, онда нақты
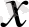 пен
пен
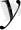 сандары берілді деп түсінуіміз керек.
сандары берілді деп түсінуіміз керек.
Егер
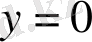 болса, онда
болса, онда
 комплекс саны
комплекс саны
 нақты бөлігіне тең, яғни
нақты бөлігіне тең, яғни
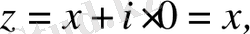 осы сияқты, егер
осы сияқты, егер
 болса, онда
болса, онда
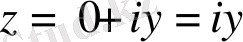 .
.
Жазықтықта
 тікбұрышты декарт координат жүйені қарастырайық және
тікбұрышты декарт координат жүйені қарастырайық және
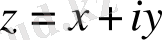 комплекс сандағы
комплекс сандағы
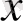 пен
пен
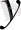 нақты сандар осы жазықтықтағы нүктенің координаттары болсын. Онда әрбір
нақты сандар осы жазықтықтағы нүктенің координаттары болсын. Онда әрбір
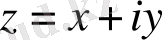 комплекс санына осы жазықтықта
комплекс санына осы жазықтықта
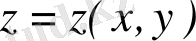 нүкте сәйкес келеді және керісінше, яғни жазықтықтағы әрбір
нүкте сәйкес келеді және керісінше, яғни жазықтықтағы әрбір
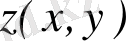 нүктеге осы жазықтықта анықталған
нүктеге осы жазықтықта анықталған
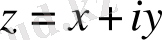 комплекс саны сәйкес келеді.
комплекс саны сәйкес келеді.
Сонымен комплекс сандар жиыны мен
 жазықтықтағы нүктелер жиыны арасында өзара бір мәнділік сәйкестік бар (1- сурет) .
жазықтықтағы нүктелер жиыны арасында өзара бір мәнділік сәйкестік бар (1- сурет) .
 жазықтығындағы әрбір
жазықтығындағы әрбір
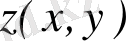 нүкте, осы жазықтықтағы координат жүйенің бас нүктесі вектордың
нүкте, осы жазықтықтағы координат жүйенің бас нүктесі вектордың
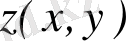 нүкте вектордың соңғы нүктесі болатын векторды анықтайды. Осылайша анықталған вектордың
нүкте вектордың соңғы нүктесі болатын векторды анықтайды. Осылайша анықталған вектордың
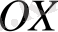 өсіндегі проекциясы
өсіндегі проекциясы
 ке, ал
ке, ал
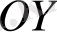 өсіндегі проекциясы
өсіндегі проекциясы
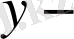 ке тең. Сонымен, кез келген
ке тең. Сонымен, кез келген
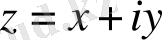 комплекс сандардың геометриялық кескінін
комплекс сандардың геометриялық кескінін
 жазықтығында
жазықтығында
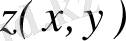 нүктелер немесе
нүктелер немесе
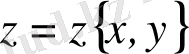 векторлар арқылы бейнелеуге болады. Осылайша анықталған
векторлар арқылы бейнелеуге болады. Осылайша анықталған
 жазықтығын комплекс сандар жазықтығы дейміз, немесе
жазықтығын комплекс сандар жазықтығы дейміз, немесе
 комплекс жазықтығы деп аталады.
комплекс жазықтығы деп аталады.
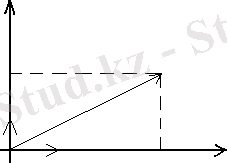
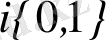
1-сурет. Бірлік векторын анықтау.
 нақты
нақты
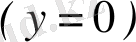 сандар
сандар
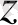 жазықтығында
жазықтығында
 өсіндегі
өсіндегі
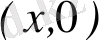 нүктелерді немесе немесе
нүктелерді немесе немесе
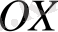 өсіндегі
өсіндегі
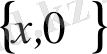 векторларды бейнелейді.
векторларды бейнелейді.
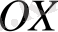 өсі нақты өс деп аталады.
өсі нақты өс деп аталады.
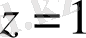 нақты саны
нақты саны
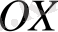 өсіндегі
өсіндегі
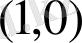 нүктені немесе осы өстегі
нүктені немесе осы өстегі
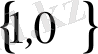 бірлік векторды анықтайды
бірлік векторды анықтайды
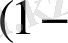 сурет) .
сурет) .
Ал
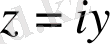 жорымал саны
жорымал саны
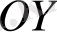 өсіндегі
өсіндегі
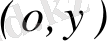 нүктені немесе осы өстегі
нүктені немесе осы өстегі
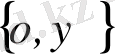 векторды анықтайды.
векторды анықтайды.
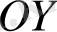 өсі жорымал өс деп аталады.
өсі жорымал өс деп аталады.
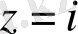 жорымал саны
жорымал саны
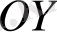 өсіндегі
өсіндегі
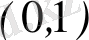 нүктені немесе осы өстегі бірлік
нүктені немесе осы өстегі бірлік
 векторын анықтайды және бұл вектор
векторын анықтайды және бұл вектор
 өсіндегі бірлік вектор болады (1- сурет) . [6]
өсіндегі бірлік вектор болады (1- сурет) . [6]
Анықтама.
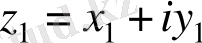 және
және
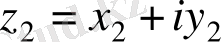 комплекс сандары тең деп аталады, егер комплекс сандардың нақты бөліктері нақты бөліктеріне, ал жорымал бөліктері жорымал бөліктеріне тең болса, яғни
комплекс сандары тең деп аталады, егер комплекс сандардың нақты бөліктері нақты бөліктеріне, ал жорымал бөліктері жорымал бөліктеріне тең болса, яғни
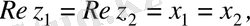
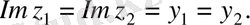
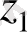 мен
мен
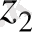 комплекс сандардың теңдігі
комплекс сандардың теңдігі
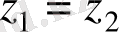 таңбамен белгіленеді.
таңбамен белгіленеді.
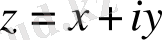 пен
пен
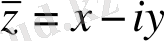 комплекс сандары өзара түйіндес комплекс сандар деп аталады. Бұл жағдайда
комплекс сандары өзара түйіндес комплекс сандар деп аталады. Бұл жағдайда
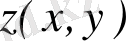 пен
пен
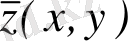 нүктелері нақты
нүктелері нақты
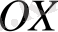 өсі арқылы симметриялы болады.
өсі арқылы симметриялы болады.
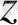 комплекс жазықтығындағы
комплекс жазықтығындағы
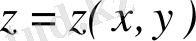 векторының
векторының
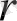 ұзындығына және осы вектордың
ұзындығына және осы вектордың
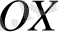 нақты өсімен оң бағытта түзейтін
нақты өсімен оң бағытта түзейтін
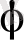 бұрышын қарастырайық (1- сурет) .
бұрышын қарастырайық (1- сурет) .
Вектордың
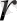 ұзындығы мен
ұзындығы мен
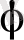 бұрышы
бұрышы
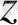 комплекс санның сәйкес модулі және аргументі деп аталады және олар былай белгіленеді.
комплекс санның сәйкес модулі және аргументі деп аталады және олар былай белгіленеді.
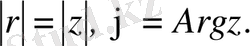 (1. 3)
(1. 3)
Бізге аналитикалық геометриядан, декарт координат пен поляр координат жүйелерінің арасындағы байланыс мына формула арқылы өрнектелінетіні белгілі:

Онда
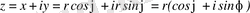 . (1. 4)
. (1. 4)
Бұл формула
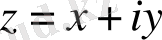 комплекс санның тригонометриялық түрі деп аталады. Осыдан
комплекс санның тригонометриялық түрі деп аталады. Осыдан
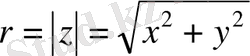 (1. 5)
(1. 5)
және
 болғанда
болғанда
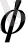 аргументтің барлық мәндері мына қатынасты қанағаттандырады:
аргументтің барлық мәндері мына қатынасты қанағаттандырады:
.
 (1. 6)
(1. 6)
Егер
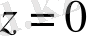 болса, онда
болса, онда
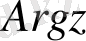 анықталмаған, сондықтан
анықталмаған, сондықтан
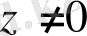 болғанда
болғанда
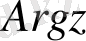 мәндерінің жиынынан
мәндерінің жиынынан
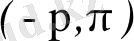 интервалға тиісті тек бір ғана мәнді бөліп аламыз және оны
интервалға тиісті тек бір ғана мәнді бөліп аламыз және оны
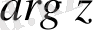 деп белгілейік және ол аргументтің негізгі мәні деп аталады:
деп белгілейік және ол аргументтің негізгі мәні деп аталады:
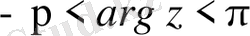 . (1. 7)
. (1. 7)
Сонда (2. 4) мен (2. 5) формулалардан мына теңдікті аламыз:
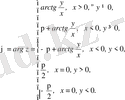 (1. 8)
(1. 8)
Онда мына теңдік орындалады:
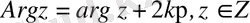 .
.
Мына нақты сандар
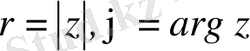 комплекс жазықтығындағы
комплекс жазықтығындағы
 нүктенің координаттары деп аталады, яғни
нүктенің координаттары деп аталады, яғни
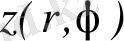 . Берілген
. Берілген
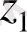 мен
мен
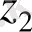 комплекс сандардың теңдігін поляр координатында
комплекс сандардың теңдігін поляр координатында
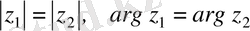 (1. 9)
(1. 9)
теңдіктерімен анықтаймыз, ал түйіндестік белгіні
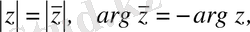 (1. 10) мұнда
(1. 10) мұнда
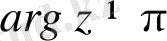 . Бізге тригонометриялық түрде екі
. Бізге тригонометриялық түрде екі
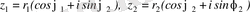 комплекс сандары берілсін. Егер
комплекс сандары берілсін. Егер
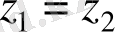 болса, онда
болса, онда
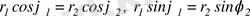
теңдіктері орындалады. Осыдан
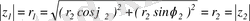 .
.
Онда жоғарыдағы теңдіктерден
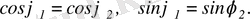
Онда
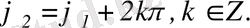
Егер
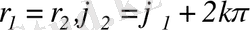 болса, онда
болса, онда
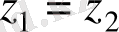 теңдігі орындалады.
теңдігі орындалады.
Мысалдар.
1.
Берілген комплекс сандарды тригонометриялық түрге келтірейік: а)
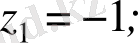 б)
б)
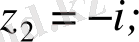 в)
в)
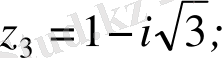 г)
г)
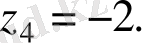
а)
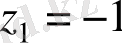 комплекс саны үшін
комплекс саны үшін
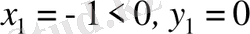 және (2. 3) формуладан
және (2. 3) формуладан
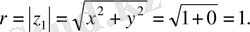
Енді (2. 6) теңдіктен
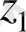 комплекс санының аргументі
комплекс санының аргументі
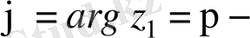 ге тең. Онда (2. 2) формула бойынша
ге тең. Онда (2. 2) формула бойынша
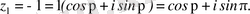
б)
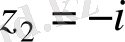 комплекс саны үшін
комплекс саны үшін
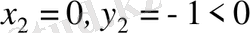 және (2. 3) формуладан
және (2. 3) формуладан
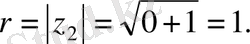 Енді (2. 6) теңдіктен
Енді (2. 6) теңдіктен
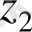 комплекс санның аргументін анықтаймыз
комплекс санның аргументін анықтаймыз
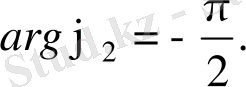
Сонда (2. 2) формула бойынша:
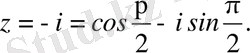
в)
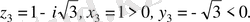 (2. 3) формуладан
(2. 3) формуладан
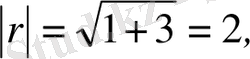 ал (2. 6) формуладан
ал (2. 6) формуладан
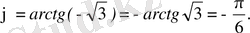 Сонда
Сонда
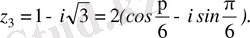
г)
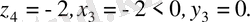 (2. 3) формуладан
(2. 3) формуладан
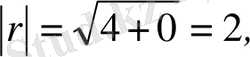 ал (2. 6) формуладан
ал (2. 6) формуладан
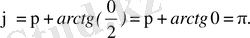 Сонда
Сонда
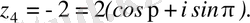
2.
Төмендегі шарттар жазықтықтағы қандай нүктелер жиындарын анықтайды: а)
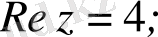 б)
б)
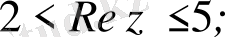 в)
в)
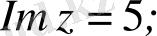 г)
г)
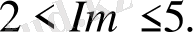
а)
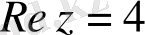 теңдігі мына теңдеумен эквивалентті:
теңдігі мына теңдеумен эквивалентті:
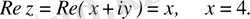
Онда
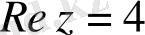 шарты
шарты
 өсіне параллель болатын
өсіне параллель болатын
 түзуінің бойындағы нүктелер жиыны болады (2а-сурет) .
түзуінің бойындағы нүктелер жиыны болады (2а-сурет) .
2- сурет. Жазықтықтағы нүктелер жиынын анықтау.
б)
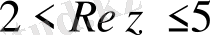 теңсіздігінен мына теңсіздікті аламыз:
теңсіздігінен мына теңсіздікті аламыз:
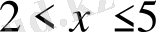 .
.
Сонымен берілген шарт
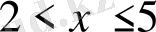 теңсіздігін қанағаттандыратын нүктелер жиыны болады (2б-сурет) .
теңсіздігін қанағаттандыратын нүктелер жиыны болады (2б-сурет) .
в)
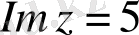 шарт
шарт
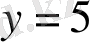 теңдеуімен эквивалентті, яғни берілген шарт
теңдеуімен эквивалентті, яғни берілген шарт
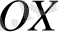 өсіне параллель болатын
өсіне параллель болатын
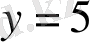 түзуді анықтайды (2в-сурет) .
түзуді анықтайды (2в-сурет) .
г)
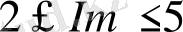 шарт
шарт
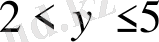 теңсіздіктен эквивалентті, сондықтан берілген шарт
теңсіздіктен эквивалентті, сондықтан берілген шарт
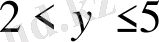 теңсіздікті қанағаттандыратын нүктелер жиыны болады (2г-сурет) .
теңсіздікті қанағаттандыратын нүктелер жиыны болады (2г-сурет) .
Комплекс сандар және олардың геометриялық кескіні. Комплекс сан z деп белгілі бір тәртіппен алынған х және у қос нақты сандар айтылады және ол алгебралық түрде z=x+іy деп белгіленеді, мұндағы x және y-нақты сандар, ал і- жорымал бірлік деп аталады, . Комплекс сандар жиыны С әрпімен белгіленеді: С= .
х саны z комплекс санының нақты бөлігі деп аталып, х=Rе z (Rееllе деген француз сөзінен алынған) арқылы белгіленеді, ал y саны z комплекс санының жорымал бөлігі деп аталып, y=Іm z (Іmаgіnаіrе деген француз сөзінен алынған) арқылы белгіленеді.
Егер
 1
=х
1
+ іy
1
және z
2
= x
2
+ іy
2
екі комплекс сандарының сәйкес нақты
1
=х
1
+ іy
1
және z
2
= x
2
+ іy
2
екі комплекс сандарының сәйкес нақты
және жорымал бөліктері өзара тең болса, яғни x 1 = x 2 , y 1 = y 2 , онда олар тең комплекс сандар деп аталады. Дербес жағдайда, z=x+іy комплекс саны нөлге тең болады, тек сонда ғана, егер x = y = 0 болғанда. Комплекс сандар үшін «артық» және «кем» ұғымдары енгізілмейді.
Бірінші компоненттері өзара тең, ал екінші компоненттерінің таңбасы ғана қарама-қарсы екі комплекс сан түйіндес комплекс сандар дейді.
Кез келген z= x+іy комплекс санын Оxy жазықтығында М(x; y) нүктесімен кескіндеуге болады (3-сурет ) .
Сонда z С санын М нүктесінің аффиксі деп, а жазықтық комплекс жазықтық (кейде Гаусс жазықтығы) деп аталады. Комплекс сандарды осылайша кескіндегенде нақты сандар абсциссалар осінің нүктелерімен кескінделеді де, ал ординаталар осінің нүктелері таза жорымал сандарды кескіндейді.
Сондықтан абсцисса осін нақты ось деп, ал ордината осін жорымал ось деп атайды.
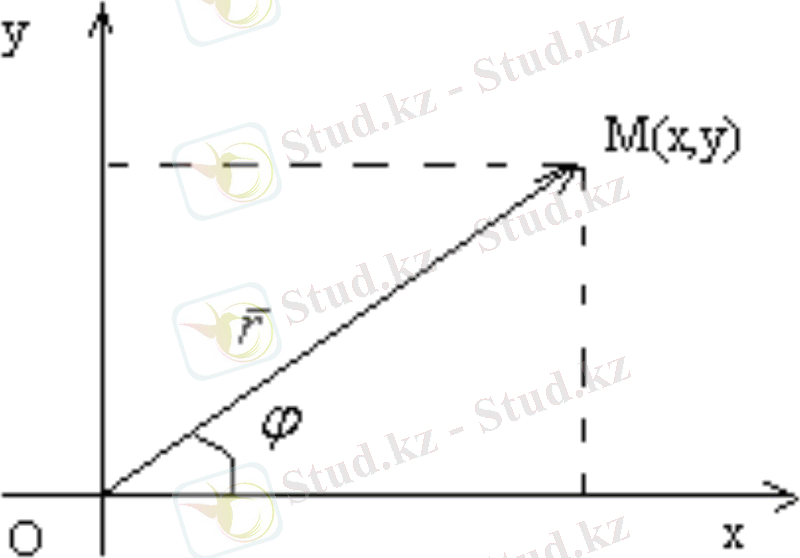
3-сурет. Түйіндес комплекс сандарды анықтау.
z=x+іy комплекс санын =О = (х, у) радиус-векторының көмегімен беруге болады. r векторының ұзындығын z комплекс санының модулі деп атайды және ол z немесе r арқылы белгіленеді:
Демек, φ - Ох осін векторының бағытымен беттестіру үшін оң бағытқа бұратын бұрышты кескіндейді, егер бұру сағат тіліне қарсы бағытта іске асырылса, онда бұл бұрыш оң, қарсы жағдайда - теріс деп есептелінеді.
z=0 комплекс саны үшін аргумент анықталмайды. Әрбір z ≠ 0 комплекс саны үшін оның аргументінің бірінен- бірінің айырмашылығы 2
 болатын көп мәндері болады.
болатын көп мәндері болады.
Ескерту. Көп жағдайда есеп шығару барысында аргументтің бас мәні
(1. 11)
формуласымен анықталады.
түрінде жазуға болады. Комплекс санының мұндай жазылуын комплекс санының көрсеткіштік түрі деп атайды.
Мысалы z 1 =-1+і және z 2 =-1 комплекс сандарын тригонометриялық және көрсеткіштік түрде жазыңыздар.
Шешуі. z 1 үшін
,
яғни . Сондықтан
z 2 үшін
... жалғасы- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz