Математикалық модельдерге қойылатын талаптар

Пән: Математика, Геометрия
Жұмыс түрі: Реферат
Тегін: Антиплагиат
Көлемі: 12 бет
Таңдаулыға:

Қорқыт Ата атындағы Қызылорда мемлекеттік университеті

Тақырыбы: Математикалық модельдерге қойылатын талаптар

Орындаған: Амангельди Жасулан
Қабылдаған: Ержанова Айгүл

Қызылорда, 2017ж
Математикалық модельдер туралы алғашқы түсінік.

Айталық, мынандай есеп берілсін . . . осындай сөздермен математикада теоремалардың, есептің шарттары басталады. Онан кейін дәл анықталған математикалық түсініктер арқылы есептің барысы баяндалады. Оны осы саланың мамандары бірдей қабылдайды.
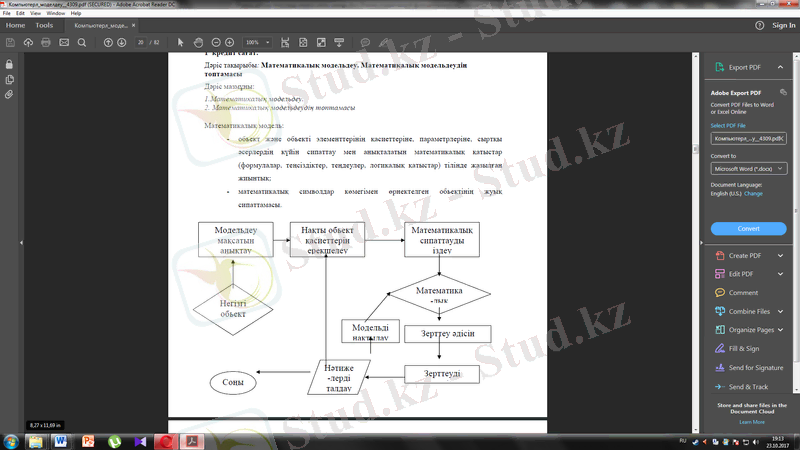
Ал қолданбалы математикадағы жағдай басқаша. Мұнда математика емес нақты (реальный) объект - жаратылыстағы құбылыс, өндірістік процесс, басқару системасы (жүйесі), экономикалық жоспар т.б. беріледі. Бұл объектілерді зерттеу үшін оларды математика тіліне аударады, яғни математикалық моделін жасайды: оның ең қажетті деген қасиеттері іріктеліп, оны математика тіліне аударады. Осыдан кейін барып математикалық модель құрылғаннан кейін, оны математиканың әдістеріне сүйене отырып зерттейді.
Енді математикалық модельдің қарапайым моделін қарастырайық.
Мысалы айталық, жазу столының бетінің ауданын табу керек болсын. Стол беті абстракты тіктөртбұрышпен алмастырылып, соның ауданы столдың бетінің ауданы деп есептеледі. Бұл жерде біз столдың ауданын, біздің сезіміміз бойынша, тіктөртбұрыштың ауданына тең деп есептедік. Бірақ біз көзбен өлшегеніміздей столдың беті тіктөртбұрыш болмауы мүмкін. Сондықтан столдың бетінің ауданын дәлірек табу үшін біз оның диагональдарын өлшейміз. Егер диагональдар тең болса, онда стол тіктөртбұрыш, ал болмаса онда столдың ауданын басқа жолмен есептеуге тура келеді. Егер столдың ауданын одан да дәлірек есептегіміз келсе, онда оның бұрыштары доғал ма, доғал емес пе, соны анықтап, егер доғал болса соны ескеру арқылы столдың бетінің ауданын есептеуге тырысамыз.
Математикалық модельдерге қойылатын талаптар: дәлдік - бұл қасиет модель көмегімен болжанған объекттің параметрлерінің мәндері ақиқат мәндермен сәйкестігінің дәрежесін көрсетеді; компьютер уақытының шығындарының тиімділігі; универсалдық яғни біртекті объектілер топтарына анализдеуге қолдануға болатындығы.

Математикалық модельдеудегі негізгі терминдер

Кез келген математикалық модель келесі: компоненттер, айнымалылар, параметрлер, функционалдық тәуелділіктер, шектеулер деп аталатын құрастырушылардың реттелген комбинациясы болып табылады.
Сәйкес ұйымдастыру амалымен жүйені құрастыратын құрамдастыру бөліктерді модель компонеттері деп түсінеді. Компоненттер бөлінбейтін құрамдастырушылар (модель "элементтері") немесе "ішкі жүйе" болып табылатын құрамдастырушылар болуы мүмкін. Әдетте жүйенің кірістері мен шығыстары айнымалылар деп, ал басқа шамалар - параметрлер деп аталады. Мұндай келісім шарт бойынша алынады. Қосымша келісімдер болмаса қайсысы айнымалы, қайсысы параметр деген сұраққа жауап табылмайды. Осындай келісім ретінде, мысалы, функциялар класы алынуы мүмкін. Айнымалыларды кірістегі және шығыстағы айнымалы деп бөлгеніміз де абсолютты болмайды. Мұндай бөлу тек қана анықталған жүйеге қолданылады. Зерттелетін жүйенің анықталған қасиеттеріне сүйену керек. Жүйе кірістері (экзогендік айнымалылар) жүйеден тыс пайда болады және сыртқы себептер әрекеттері нәтижесінен туады; жүйе шығыстары (эндогендік айнымалылар) экзогендік айнымалылар жүйеге әсер еткен себебінен жүйеде пайда болады.

Математикалық модельдердің бас құрастырушылары - функционалдық тәуелділіктер. Олар жүйенің немесе компоненттің айнымалыларының және параметрлерінің жүріс-тұрысын бейнелейді. Әдетте олар экзогендік (х) және эндогендік (у) айнымалылар немесе айнымалылар және олардан тәуелді параметрлер (р) арасындағы ішкі қатынастарды орнатады:
а) y = φ(p,x),
б) р = ψ(x,y).
φ функциясы көбінесе операторлық (немесе оператор), ал ψ функциясы - параметрлік деп аталады. Жүйенің жұмысының заңы аналитикалық, графикалық, кестелік, т.б. түрде берілуі мүмкін. Модельдердің соңғы құрамдастырушысы - шектеулер. Қарапайым кезде шектеулер деп модель аргументтерінің векторының өзгеру аймағын түсінеді x Dx. Модель параметрлері де кейбір рұқсат етілген аймақта берілуі мүмкін p Dp. Көбінесе модельденетін жүйе қоршаған ортаға әсер етпейді деп белгіленеді. Қоршаған ортаның әсерін есепке алмау негізделген болуы керек.

Математикалық модельдерге қойылатын талаптар

Конструкцияның, технологиялық процестердің және оның элементтерінің математикалық моделі (ММ) дегенде талап етілген дәлдікпен оқытатын объектті және оның өнеркәсіптік жағдайларда өзін ұстауын сипаттайтын математикалық қатынастардың жүйесін түсінеміз. Математикалық модельдерді тұрғызу кезінде объектті сипаттаудың әртүрлі математикалық құралдарын - көптік теориясы, графтар теориясы, ықтималдықтар теориясы, математикалық логиканы, математикалық бағдарламалауды, дифференциалдық және интегралдық теңдеулерді және т.б. қолданады.
Математикалық модельдерге жоғары дәлділіктің, экономикалықтың және әмбебаптылық талаптар қояды.
Математикалық модельдің экономикалықтығы машинаның уақытты шығындарымен (ЭЕМ жұмыстары) анықталады. Математикалық модельдің әмбебаптылық деңгейі технологиялық процестердің және олардың элементтерінің үлкен санының талдауы үшін оларды қолдану мүмкіндігіне байланысты. Математикалық модельдің дәлділігіне, экономикалықтығына және әмбебаптылық деңгейіне деген талаптар қарама-қайшы. Сондықтан сәтті ымыралы шешімге ие бола керек.
Математикалық модельдерге қойылған негізгі талаптар теңбе-теңділік, әмбебаптылық және экономикалық талаптары болып табылады.
Теңбе-теңділік. Егер қабылданған дәлділікпен объект енгізілген қасиеттерін бейнелейтін болса, модель теңбе-тең деп есептеледі. Дәлділік модельдің немесе объекттің шығыс параметрлерінің мәндерінің сәйкестігі деңгейі секілді анықталады. εj-шығыс параметріне j- бойынша модельдің салыстырмалы қателігі:
. (1)
Мұндағы - модель көмегімен есептелінген j-ші шығыс параметрі; yj- модельденетін объектте бар дәл сондай шығыс параметрі.
Есептелінетін шығыс параметрлерінің жиынтығы бойынша Е моделінің қателігі вектор нормаларының бірімен есептелінеді Е=(ε1,ε2,...εm).
. (2)
Шарты орындалатын облысты ерекшелеуге болады. Бұл модельдің облысы теңбе-теңдік облысы (ТО) деп аталады. Әрбір шығыс параметрі үшін ε шек индивидуальды шектік мәнді ендіру және ТО анықтау, бір мезгілде εj ε шек түрдің барлық m жағдайлары орындалатын облыс секілді мүмкін болады.
Нақты модельдер үшін теңбе-теңдік облысын анықтау - үлкен есептеуіш шығындарды талап ететін күрделі процедура. ТО көрсетілімінің бұл шығындары мен қиындықтары сыртқы параметрлер кеңістігінің өлшемінің ұлғаюымен жылдам өсуде. ТО анықтау - күрделі тапсырма, мысалы, параметрикалық тиімділіктің есептеріне қарағанда. Унифицирленген элементтер моделі үшін теңбе-теңдік облыстар есебі ТО анықтаудың бір реттілігі мен және әртүрлі жүйелерді жобалау кезінде оларды қолданудың көп реттілігіне байланысты анықталған болып келеді. ТО білу бар элементтер қатарынан модельдерді таңдауға және сонымен қатар машиналық есептердің нәтижелерінің сенімділігін ұлғайтуға мүмкіндік береді.
Элементтер моделінің кітапханасына модельдерді орындайтын алгоритмдер мен параметрлердің номиналды мәндерінің қасына теңбе-теңдік облысын беретін, q'k және q''k, сыртқы параметрлерінің шекаралық мәндері қосылуы тиіс.
Әмбебаптылық. ТО анықтау кезінде сыртқы параметрлердің жиынтығы және модельде есептелінетін қасиеттерді бейнелейтін уj шығыс параметрлерінің жиынтығын таңдау керек. Осы кезде типтік сыртқы параметрлер жүктеме параметрлер және сыртқы әрекеттердің (электрлік, механикалық, жылулық, радиационалдық және т.б) параметрлері болып табылады. Есептелінетін сыртқы факторлардың санының өсуі модельдің қолданушылығын кеңейтеді, бірақ ТО анықтау бойынша жұмысты елеулі түрде көтереді. Шығыс параметрлерінің жиынтығын таңдау сондай-ақ бірдей мәнді емес, алайда көптеген объекттер үшін ескерілетін қасиеттердің (саны мен реті) және оларға сәйкес шығыс параметрлерінің (саны мен реті) салыстырмалы түрде үлкен емес, айтарлықтай тұрақты және шығыс параметрлерінің типтік жиынын құрайды. Мысалы, БИС логикалық элементтерінің макромодельдері үшін мұндай шығыс параметрлері "0" и "1" логикалық жағдайындағы шығыс кернеуінің деңгейлері, кедергі қарсы тұрушылар қорлары, сигналды таралуының кідірісі, себілетін қуат болып табылады.
Экономдылық. Модельдің үнемділігі оны орындау үшін есептеуіш ресурстарының шығындарымен, соның ішінде машиналық уақыт Тм және жадысы Пм шығындарымен есептелінеді. ААЖ-да қандайда бір жобалы процедураны орындауда жалпы шығындар Тм және Пм таңдалған модельдер ерекшелігіне секілді, шешімдер тәсіліне де байланысты.
Көптеген жағдайларда сандық тәсілді орындау кезінде модельденетін объект құрамына кіретін элемент моделіне көп ретті қатынас жүреді. Онда элемент моделін модельге қатынасу кезінде машиналық уақыттың шығындарымен сипаттауда үнемді, ал модельге қатынасу саны шешімнің тәсілін үнемдеу бағасы кезінде есептелуі керек. Жадының шығындары бойынша модельдің үнемділігі модельді орындау үшін қажетті оперативті жадының көлемі мен бағаланады. Бір жағынан теңбе-теңдіктің кең облыстарының талаптары, әмбебаптылықтың үлкен деңгейі, екінші жағынан жоғары экономикалық қарамы қайшы. Осы талаптардың ымыралы қанағаттандыруы әртүрлі қолданыста бірдей болмайды. Бұл жағдай ААЖ-да бірдей типті объектілер үшін көптеген модельдердің - макромодельдердің, көп деңгейлік, аралас модельдердің әр түрлі тегін қолдануды игереді.

Математикалық модельдердің негізгі түрлері

Қолданудың әртүрлі аспектілерін қанағаттандыратын жалпы универсалды модельді жасау мүмкін емес. Басқарылатын объекттің кейбір қасиеттерін қамтып көрсететін ақпаратты алу үшін модельдерді классификациялау қажет.
Классификациялаудың негізінде φ оператордың ерекшеліктері жатады. Уақыттық және кеңістіктік белгілері бойынша басқару объекттердің барлық түрлерін келесі кластарға бөлуге болады: статикалық немесе динамикалық; сызықты немесе сызықты емес; уақыт бойынша үздіксіз немесе дискретті; стационарлы немесе стационарлы емес; параметрлері кеңістік бойынша өзгеретін процестер және параметрлі кеңістік бойынша өзгермейтін процестер. Математикалық модельдер сәйкес объектілерді суреттейтін болғандықтан, оларға да осы кластарды қолдануға болады. Модельдің толық атауына айтылған белгілердің барлығы кіруі мүмкін. Осы белгілер модельдердің сәйкес типтер атауларының негізі болып табылды.
Жүйеде зерттелетін процестер сипаттарына сәйкес модельдердің барлығын келесі түрлерге бөлуге болады.
Процесте кез келген кездейсоқ әсерлер жоқ деп есептелсе, процесс детерминерленген (анықталған) деп аталады; осындай процестерді бейнелейтін модельдер - детерминерленген модель болады.
Ықтималдық процестер мен оқиғаларды бейнелейтін модельдер стохастикалық модель деп аталады; бұл кезде кездейсоқ процестің бірсыпыра іске асырылуы болжанып, орта сипаттамалары бағаланады.
Стационарлы және стационарлы емес модельдер. Егер де φ оператордың түрі және оның p параметрлері уақыт бойынша өзгермесе, яғни келесі орындалса
φ[p(t),x]= φ[p(t+τ),x], яғни y= φ(p,x)
онда модель стационарлы болып табылады.
Егер де модель параметрлері уақыт бойынша өзгеретін болса
y= φ[p(t),x]
модель параметрлік стационарлы емес.
Уақыттан функция түрі де тәуелді болса, бұл жағдай стационарлы еместіктің ең жалпы түрі болады. Бұл кезде функцияға тағы бір аргумент қосылады:
y= φ(p,t,x)
Статикалық және динамикалық модельдер. Модель түрлерін осылай бөлгеннің негізінде зерттелетін объекттің материалды жүйе ретінде қозғалысының ерекшеліктері жатады.
Басқару есептер көзқарасы жағынан модельдер туралы әңгімелесек, кеңістік деп геометриялық кеңістікті атамайтынымызды еске алу қажет. Бұл кезде кеңістік деп күй кеңістігін, яғни шығудағы у айнымалыларының күй координаталарын түсінеміз. у векторының элементтері ретінде әдетте бақыланатын технологиялық параметрлер (шығын, қысым, температура, ылғалдық, тұтқырлық, ж.б.) болады. у векторының элементтерінің құрамы объекттің өзі үшін (модельге қарағанда) толығырақ болуы мүмкін, себебі модельдеу кезде нақты объекттің қасиеттерінің тек қана бір бөлігін оқу қажет. Күй кеңістігінде және уақыт бойынша басқару объекттің қозғалысы y(t) векторлық процесс көмегімен бағаланады.
Егер де жүйе күйі өзгермесе, яғни жүйеде тепе-теңдік орындалса, жүйе моделі статикалық деп аталады, бірақ қозғалыс тепе-теңдіктегі объекттің статикалық күйімен байланысқан. Статикалық модельдердің математикалық бейнелеуіне айнымалы ретінде уақыт кірмейді, бұл ... жалғасы

Сіз бұл жұмысты біздің қосымшамыз арқылы толығымен тегін көре аласыз.