Экономикалық - математикалық модель құру және оның қолданылу

Пән: Экономика
Жұмыс түрі: Реферат
Тегін: Антиплагиат
Көлемі: 14 бет
Таңдаулыға:

Мазмұны

I. Кіріспе . . . 2

II. Теориялық бөлім . . . 3

2. 1 Экономикалық- математикалық модель құру және оның қолданылуы. . 3

III. Тәжірибелік бөлім . . . 6

3. 1 Матрицалы экономика-математикалық үлгілеулер6-12

IV. Қорытынды . . . 13

V. Пайдаланылған әдебиеттер . . . 14

Матрицалық, экономикалық, математикалық модельдеу

I Кіріспе

Модельдеу әдісі - ғылыми танымның зерттеу объектілерін олардың модельдерін жасап, зерделеу арқылы танып-білу әдісі. Модельдеу әдісінің пайда болуы техникалық жүйелердің күрделілігіне, материалдық процестер мен құбылыстарды зерттеу қажеттілігіне орай туындайтын ой-түрткілерге, себептерге, тағы басқа байланысты. Модельдеу кез келген затты мақсатты, жылдам, неғұрлым тиімді тәсілмен зерттеуге мүмкіндік береді. Сонымен қатар, модель зерттеліп жатқан объектінің субъект баса көңіл қойып отырған қасиеттерін жоғары дәлдікпен бейнелей алады. Ол объектіні құбылыстарға, заттар мен процестерге тән қосалқы белгілерден айырып, ондағы жалпы, негізгі, елеулі заңды белгілерді табуға мүмкіндік береді. Сондықтан модельдеу танымның формасы, әдісі, ірі категориясы болып саналады.

Модельдеу екі түрге бөлінеді: 1) Пәндік модельдеу зерттеу объектісінің белгілі бір физикалық, геометриялық, динамикалық немесе функционалдық сипаттамаларын нақыштайтын модель жасау арқылы іске асады. 2) Идеалды модельдеу кезінде модель ретінде сұлбалар, сызбалар, формулалар, табиғи және жасанды тілдердегі сөйлемдер, тағы басқа қолданылады. Мұндай модельдеу түріне математикалық (компьютерлік) модельдеу жатады. Әлдебір құбылысты оның моделі арқылы зерделеу модельдік эксперимент деп аталады. Күрделі жүйелерді зерттеу кезінде көбіне бірін-бірі толықтыратын бірнеше модельдер қолданылуы мүмкін. Кейде бір құбылысты зерттегенде бір-біріне қарама-қайшы келетін модельдер пайдаланып, бұл қайшылық таным дамуының аса жоғары деңгейінде шешімін табуы мүмкін. Модельдеу танымның басқа да формалары мен әдістерімен (эксперимент, абстрактілеу, гипотеза ұсыну, теория құру, түсініктемелеу, тағы басқа) бірлесе отырып, адам білімінің тереңдей түсінуіне зор ықпал етеді.

Математикалық модельдеу - кез келген құбылыстарды немесе күрделі физ. процестерді, аппараттарды олардың математикалық модельдерін құру арқылы зерттеу тәсілі; матем. модельді құру процесі. Матем. модель деп қажетті процесті немесе аппаратты сипаттайтын матем. теңдеулер жүйесін айтады. М. м. үшін кез келген матем. мүмкіндіктерді (дифференциалдық немесе интегралдық теңдеулерді, жиындар теориясын, абстрактылық алгебраны, матем. логиканы, ықтималдықтар теориясын, т. б. ) пайдаланады. М. м. негізіне түпнұсқа мен модельдің айнымалы параметрлерінің біртектес немесе ұқсас теңдеулермен сипатталуы алынады. М. м., көбінесе, компьютерлер арқылы зерттеледі, сондықтан оны кейде компьютерлік модельдеу деп те атайды

II Теориялық бөлім

2. 1 Экономикалық - математикалық модель құру және оның қолданылуы

Модельдеу ғылыми зерттеу барысында ерте заманнан қолданылып, біртіндеп ғылымның көптеген саласында қамти бастады. Мысалы: техникалық құрастырулар, құрылыс және архитектура, астрономия, физика, биология және де қоғамдық ғылымдар. Бір жүйе, бір терминология жоқ болғандықтан, кейіннен ғана модельдеудің рөлін және оның универсалды тәсіл екенін түсіндік. Модельдеу әдістері ұзақ уақыт басқа ғылым салаларына бағыныңқысыз өзгеше дамыды. Қазіргі таңда “модель” термині кеңінен қолданылады, тіпті бірнеше магынағада ие. Біз өзімізге терең білім алуымызға қажетті ғана модель түрін қарастырамыз. Модель - бұл зерттеу барысында жаңаша білім беретін материалды немесе ойша ұсынылатын объект. Модельдің негізгі қасиеттерін ерекшелеп айтсақ: модельдің қарапайым түрі, модельдің толықтырылған түрі, модельдің адекваттық түрі. Модельдің қарапайым түрі: бұл қарапайым сөзбен айтқанда экономикалық жүйенің дамуына кері әсер етіп қиындық туғызатын айнымалылар емес, математикалық аппараттың қарапайымдылығы. Модельдің толықтырылған түрі: құрамына көздеген мақсатқа жетудегі барлық факторларлар, барлық есеп шарттары кіреді. Адекваттық модель түрі бұл көздеген мақсатқа дәлме-дәл нақтылықпен жету мүмкіндігі. Модельдеуге кеңірек тоқталсақ бұл зерттеу мен құрастыру жүйесі болып табылады, ол абстракция, аналогия, гипотеза сиякты санаттармен тығыз байланысты. Модельдеу үрдісі абстракты ойлау, аналогиялық негіздерге сүйеніп ой жинақтау және ғылыми жорамалдарды орнымен құрастыру болып табылады. Модельдеудің басты ерекшелігі орнын басар нысан көмегімен ортаны тану тәсілі. Бұл жерде модель зерттеу нысаны мен зерттеуші арасында құрал ретінде қолданылып тұр. Дәл осы ерекшелік модельдеуде жорамалды түрде қолдану тәсілдерін анықтайды.

Ал оны зерттеу өзара байланыспен, кезеңдерден тұратын үлкен еңбекті қажет етеді:

есептің қойылуы
белгілі жобаны құру
модельді құру
модельді зерттеу
модельді тексеріп және нәтижені бағалау
нәтижені енгізіп оның дұрыстығын тексеру

Экономика - математикалық модельді құрастыру кезінде төменде көрсетілген талаптарды қатаң сақтаған жөн: Модель қатаң түрде ғылыми экономикалық теорияға, белгілі бір заңдылықтарды ашатын санаттарға негізделіп жасалу қажет .

Модель модельденіп жатқан үрдістің нақты құрылымын немесе сол

құрылымның негіздеріне сай нысанның құрылымын көрсетуі керек .

Модельде көлемнің бірлігі қамтылып және экономикалық заңдылықтар

сақталуы керек.

Модельде басқарылатын, жартылай басқарылатын және параметрлерді

нақты ажыратулар жүргізілуі керек.

Модель қолданылу шекарасына және нысанға сәйкес келу шарттарын

қанағаттандыруы қажет.

«Инфляция және жұмыссыздық» моделі мысалында экономика-математикалық модельді қолдануды қарастырайық. Кеңінен қолданылып жүрген тұжырымдар негізінде жұмыссыздық пен инфляция арақатынасын зерттеуде Филлипс қисығының көмегіне жүгінеміз, ол жалақының өсу қарқыны мен жұмыссыздықтың өсу қарқыны арасына байланыс орнатады. ал - жалақының өсу қарқыны жұмыссыздықтың өсу қарқыны. Инфляцияның өсу қарқынына және баға деңгейінің өсу қарқынына мынадай белгілеулер енгізізіп ал еңбек өнімділігін арқылы белгілеп мына түрге келеміз. Жалақы көлемін азайту жұмыссыздық қарқынының өсуіне сызықты бағыныңқы деп есептесек, яғни Филлипстің адаптерленген қисығына ие боламыз. Кейініректе қаржыгерлер Филлипс қисығының ұсыныс кезінде жалақының өсу қарқыны болатын басқа түрін қолдануды ұйғарды, бұл жерде күтіліп отырған инфляция қарқыны. Демек, арақатынаспен бірге Филлипс қисығы мынадай түрге ие болады. Күтіліп отырған инфляция қарқыны туралы болжам мына түрге келеді. Номиналды ақша теңгерімін арқылы және оның өсу қарқынын деп белгілей отырып, түрге келеміз. Бұл алынулар нақты ақшаның өсу қарқынын көрсетеді. Қарастырып отырған теңдеулер құрамында белгісіз үш айнымалысы бар «инфляция - жұмыссыздық» жабық модель түрін көрсетіп тұр. Үш белгісіз (2) - ші теңдеумен байланысты болғандықтан екі теңдеу жүйесін құрамындағы екі айнымалымен жазуға болады. (2) - ші теңдеуді (3) және (4) теңдеулер орындарына әкеліп қойып мынандай теңдеу жүйесін аламыз:Егер біз (5) - ші теңдеу жүйесін t бойынша дифференциалдап, туындыларын (5) - ші теңдеу жүйесінен тағыда алсақ онда айтарлықтай қысқартулардан кейін тұрақты коэффициенті бар екінші дәрежелі дифференциалдық теңдеу аламыз:(6) Соңғы теңдеуіміз белгілеу жағынанда мына теңдеумен сәйкес келеді:иілу пропорционалдық коэффициенті, тербеліс жиілігі) бұл теңдеу ортаға түпкілікті қарсы күш әсері болған кезде маятник тербелісінің жиілігін сипаттайды. Ортақ шешімі біртекті дифференциялдық теңдеуден тұратын дифференциалдық теңдеудің ортақ шешімін табайық :(7) және болғандағы біртекті емес (6) - шы дифференциалдық теңдеудің дербес шешімін табамыз. (7) - ші дифференциалдық теңдеудің характеристикалық теңдеуі түбірлері болатын мына түрге келеді: (8) Нәтижесінде (6) - шы дифференциалдық теңдеудің шешімі мына түрге келеді:(9) Зерттеуден көретініміз, ұмтылғанда күтіліп отырған инфляция қарқыны тұрақты түрге келіп, номиналды ақша теңгерімінің өсу қарқыны - ге тең болады. Алынған (9) - шы формула (1) - ші Филлипс қисығымен бірге экономист мамандарға «инфляция-жұмыссыздық» динамикалық модель тербелісін тереңірек зерттеуге жол ашады. Математикалық маятник тербелісі терең зерттеліп, көптеген кітаптарда жазылған мәліметтермен сәйкес келеді, осылай зерттеу жолдары арқылы математикалық маятник моделі «инфляция - жұмыссыздық» моделімен байланысты болды. Қорыта келе экономикада көптеген үрдістер көпше түрде кездеседі, олар бір рет немесе бірнеше реттік зерттеулерде табылмайтын белгілі заңдылықтармен сипатталады. Сондықтан экономикадағы модельдеу жұмыстары көп зерттеулерді қажет етеді. Бұл мақаланы жазу кезінде мен, тек қана математикалық модельдерді біліп қана қоймай, сонымен қатар модельдер мен модельдеуді ажырата білдім. Модельдердің көптеген түрлерімен танысып, қандай есептерде қолданылатынын ұғындым. Жалпы экономикалық-математикалық модельдеудің классификацияларын анықтадым. Келешекте нарық жүйесінде, бизнесте, халық шаруашылығының кез келген саласының маманы математикалық модельдеу әдістемесін өз ісіне қолдана білуге тиіс деп есептеймін.

III ПРАКТИКАЛЫҚ БӨЛІМ

3. 1Матрицалы экономика-математикалық үлгілеулер

Жолдарының саны мен бағаналары санының бірі немесе екеуі де шексіз болатын матрицаны шексіз матрица деп түсінеміз. Бір ғана жолдан немесе бір ғана бағанадан тұратын матрицалар да болады.
а _іі диагональ элементтері ғана нөлден өзгеше болатын квадрат матрицаны диагональ М. деп аталып, dіag(а ₁ … аn) таңбасымен белгіленеді. Диагональ матрицаның барлық элементтері (а _і =1) болса, бірлік матрица деп аталады. Егер барлық (а _і =а) болса, онда скаляр матрица шығады. Барлық элементтері нөлге тең М. нөлдік М. деп аталады.

Жолдары мен бағаналарын ауыстыру арқылы алынған матрица транспозицияланған матрица деп аталып, А немесе АТ арқылы белгіленеді. Егер матрицаның элементтерін комплекс түйіндеске ауыстырсақ, онда комплекс түйіндес матрицасы шығады. Егер А транспозицияланған матрица элементтерін комплекс түйіндеске ауыстырсақ, онда А матрицамен түйіндес болатын А* матрицасы шығады.

Квадрат матрицаның анықтауышы A немесе det A деп белгіленеді.

Үшбұрыштағы матрица

Матрицаларға амалдар қолдану. Матрицаға қосу, көбейту алгебралық амалдар қолданылады. А тікбұрышты (m, n) матрицасының санына көбейтіндісі деп барлық а _іj элементтерін санына көбейткенде шығатын матрицаны айтады: Бұл амалдар:

А+В=В+А,

А+(В+С) =(А+В) +С,

( + ) А= = А+ А,

(А+В) =А+В,

(А) =(А) қасиеттерін қанағаттандырады.

Матрицаның қосындысы оның құраушыларының қосындысына тең. Матрицаны көбейту амалы 1-көбейткіш бағаналарының саны 2-көбейткіш жолдарының санына тең тікбұрыштыматрицалар үшін ғана орындалады.

(mp) өлшемді А матрицаның (pn) өлшемді В матрицасына көбейтіндісі элементтері

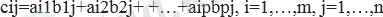
болатын (m n) өлшемді C матрицасы болып табылады. Матрицаларға енгізілген үш амал сандарға қолданылатын амалға жақын. АВ және ВА матрицаларының көбейтіндісі бірінші ретті квадрат М. Үшін ғана анықталады және көбейткіштердің ретіне де байланысты, яғни АВ=ВА орындалмай қалуы да мүмкін. Егер АВ=ВА болса, онда А және В матрицалары ауыспалы деп аталады. Әрбір көбейткіші нөлден өзгеше болса да, екі матрицаның көбейтіндісі нөлдікматрицаға тең болуы мүмкін. Сонда

М. үшін 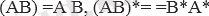ережелері орындалады. Екі квадрат матрицаның көбейтіндісінің анықтауышы көбейтілетін матрицалар анықтаушының көбейтіндісіне тең. Егер анықтауышы нөлге тең болмаса , онда А=(а _іj ) квадрат матрицасы өзгеше емес деп, ал кері жағдайда ерекше матрица деп аталады. Кез келген өзгеше емес матрицаның АА-1=Е теңдеуімен анықталатын бір ғана кері А-1 матрицасы болады. Бірдей n ретті А және В квадрат матрицалары ұқсас матрицалар деп аталады.

К өрісіндегі коэффициенттері а ₀ , а ₁ , …, a _n болатын n дәрежелі кезкелген P _n (t) =а ₀ t _n + +а ₁ tn-1+…+аn-1t+аn көпмүшесі Х квадрат М-нан P _n (Х) = а ₀ Х _n +а ₁ Х _n -1+…+а _n -1 Х+а _n Е функциясын анықтайды. Егер f(t) аналит. Функциясы барлық комплекс жазықтықта жинақталатын қатары арқылы анықталатын болса, онда функция М-нан қарастырылады. Бұл қатар кез келген квадрат М. үшін жинақты болады. М. сызықтық алгебрада, векторлық кеңістікте сызықтықбейнелеуді зерттегенде, сызықтық және квадраттық тұлғаларда, сызықтық теңдеулер системасында қолданылады. Анализ дедифференц. теңдеулерді интегралдау жүйесіне, ықтималдықтар теориясында, кванттықмеханикада, т. б. пайдаланады.

Қосымша тапсырма:

1-тапсырма. Тағайындаулар туралы есептер

Тағайындаулар туралы есептерді шешудің мысалын қарастырайық. Төрт жұмысшы жұмыстың төрт түрін орындай алады. j-й жұмысының i-м жұмысшымен 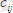орындауының бағасы 9. 4 суретте A1:D4 диапазонының ұяшықтарында келтірілген.

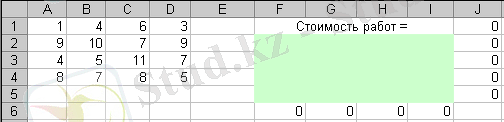
1-сурет - Тағайындаулар туралы есебіндегі жұмыстардың бағалары

Бұл кестеде жолдар жұмысшыларға сәйкес келеді, ал баған - жұмыстарға. Барлық жұмыстар орындалғандай етіп, әрбір жұмысшы тек бір жұмыста ғана болатындай етіп, ал барлық жұмыстардың орындалуының жиынтық бағасы минималды болатындай етіп жұмыс орындау жоспарын құру керек. Берілген есеп теңгерілген, яғни жұмыс саны жұмысшылар санына тең екенін атап көрсету керек. Егерде есеп теңгерілмеген болса, онда оны шешудің алдында есепті теңгеру керек, ол үшін жұмыстың жоғары құндары бар жетпейтін жолдардың немесе бағандардың санын енгізу керек.

Берілген есепті шешу үшін оның математикалық моделін құрайық. Егер i жұмысшымен j жұмысы орындалса, онда 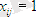, егерде i жұмысшымен j жұмысы орындалмаса, онда 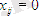. Онда модель келесі түрге ие:

Шешімді іздеу құралдарының көмегімен бұл есепті шығару үшін белгісіздерге F2:I5 ұяшықтарының диапазонын бөлейік. J1ұяшығына жұмыстардың бағасын есептейтін мақсаттық функцияны енгіземіз:

=СУММПРОИЗВ(F2:I5; A1:D4),

9. 5 суретте көрсетілгендей шектеулердің сол жақтарына сәйкес келетін формулаларды енгіземіз.

2-сурет - Тағайындаулар туралы есептегі шектеулердің сол жақтары

Бұдан кейін Сервис, Поиск решения командасын таңдаймыз және ашылған Поиск решения сұхбат терезесін 1суретте көрсетілгендей толтырамыз.

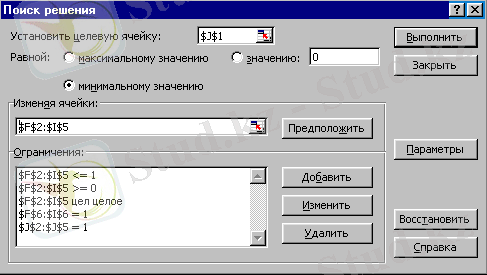
3-сурет - Тағайындаулар туралы есебінің Поиск решения сұхбат терезсі

Параметры поиска решения сұхбат терезесінде Линейная модель флажогын орнатуды ұмытпаңыз. Выполнить батырмасын басқаннан кейін шешімді іздеу құралы 2 суретте келтірілген тиімді ешімді табады.

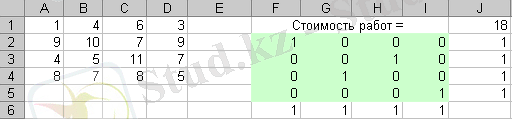
4-сурет- Тағайындаулар туралы есебіндегі жұмыстардың тиімді жоспары

2-тапсырма:

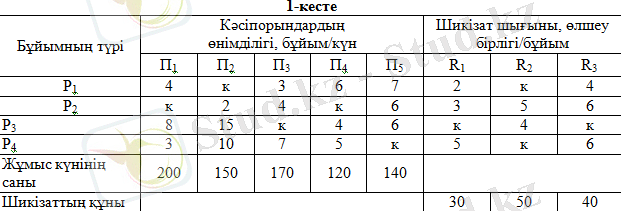
Үш түрлі шикізат тұтынып өнімнің төрт түрін шығаратын бес кәсіпорынның күн сайынғы өнімділігі, сондай-ақ әрбір кәсіпорынның жұмысының жыл бойындағы ұзақтығы және шикізаттың әрбір түрінің бағасы 1-кестеде келтірілген.

Мыналарды:

әрбір кәсіпорынның әрбір бұйым түрі бойынша жылдық өнімділігін; әрбір кәсіпорынның әрбір шикізат түрі бойынша жылдық қажетін; әрбір кәсіпорынға межеленген жұмыс күні ішінде көрсетілген бұйымның түрлерін шығаруға қажетті шикізат сатып алуға арналған жылдық кредиттеу сомасын табу қажет.