Симплекс әдісі: сызықтық программалау теориясы мен практикасындағы әдістер


Жұмыс түрі: Материал
Тегін: Антиплагиат
Көлемі: 12 бет
Таңдаулыға:
Мазмұны
І. Кіріспе . . . 2
ІІ. Теориялық бөлім … . . . 3
2. 1. Симплекс әдісі туралы түсінік . . . 3
ІІІ. Практикалық бөлім . . . 8
3. 1. Тапсырмаларды шешудің симплекстік әдістері . . . 8
IV. Қорытынды . . . 14
V. Пайдаланылған әдебиеттер тізімі . . . 15
І. Кіріспе
Қазіргі технологиялар ақпараттың кез келген көлемін орналастырудың, сақтаудың, өңдеудің және кез келген қашықтықтарға тасымалдаудың шексіз мүмкіндіктерін береді.
Кез келген оқыту түрінің, оның ішінде қашықтан оқыту ісінің тиімділігі мынадай факторларға тығыз байланысты болады, олар: оқуды ұйымдастыру технологиясы, оның техникалык базасы, жасалған әдістемелік материалдардың тиімділігі Осындайда атқарылып жатқан жұмыстар бұрында да болған сияқгы болып көрінеді. Әрине, автоматтандырылған оқыту түрі де осылай басталған. Автоматтандырылған оқыту ісіндегі теориялық бастамаларды қазіргі кездегі компьютерлік оқыту тәсілдеріңде де қолдану қажет, бірақ мұнда техника мен телекоммуникациялық байланыстардың жаңа дидактикалық мүмкіндіктерін есепке алып отыру керек. Компьютерлік оқыту программадары мен жаңа ақпараттық білім құралдарын жасау және пайдалану қазіргі оқыту технологияларымен бірге қолданылып, біте қайнасуы шарт.
ІІ. Теориялық бөлім
2. 1. Симплекс әдісі туралы түсінік
Математикалық ықшамдауда, Данцигтің симлекс алгоритмі (немесе симлекстік әдіс) сызықтық программалауда кеңінен таралған алгоритм. Информатика төңiрегiндегi техникалық есептеуiш журналы (The journal Computing in Science and Engineering) бұл алгоритмді 20 ғасырдың он мықты алгоритмдерінің біреуіне жатқызды. Алгоритм аты Т. С. Мотцин айтып кеткендей жеңіл (simplex) деген сөзден шыққан. Симплекс әдістерде қолданыс таппайды, бірақ ол симплексациялық конустарға ісерін тигізеді, қосымша шектеулермен симплекстерге тиісті болады. Конусты симплексті қарау бұрыш яғни бұрыштарының жаны геометриялық дене, көпжақ.
Сызықтық программалауды стандартты түрдің ьіреуіне келтіру келесі түрде іске асуы мүмкін. Біріншіден, барлық нөлден басқа мәні кіші мүшеге жаңа мүше енгізілуі мүмкін. Шын мүше жаңа мүше арқылы шеттелуге болады.
Екінші теңдеу x 1 мүшесін сызықтық программадан шығарылуы үшін қолданыс табады. Осылайша кіші мәнді шектеулер оң мәнді шектеулерге айналады. Екіншіден, әр бір қалып отырған шектеулер үшін «жалған айнымалы» еніп отыр, олар шектеулерді теңдікке ауыстыру үшін кіргізіледі. Бұл айнымалы теңсіздіктің екі жағындағы айырмашылықты көрсетеді және бұл айнымалы оң болады деп санаймыз.
{\displaystyle {\begin{aligned}x_{2}+2x_{3}&\leq 3\\-x_{4}+3x_{5}&\geq 2\end{aligned}}}{\displaystyle {\begin{aligned}x_{2}+2x_{3}+s_{1}&=3\\-x_{4}+3x_{5}-s_{2}&=2\\s_{1}, \, s_{2}&\geq 0\end{aligned}}}Бұл түрде алгебралық тұрғыда амалдар қолдану жеңіл болады. «≥» пайда болатын теңсіздіктерде көптеген авторлар "мол айнымалысына" жүгінеді. Үшіншіден, шектеусіз мүше сызықтық программалауда теңсіздіктен шығады. Екі әдіспен іске асыруға болады. Бір жолы мүше кездескен теңсіздікте айнымалы енгізу арқылы, екінші жолы мүшені екі шегі бар мүшемен алмастыру болып табылады. Мысалы, егер z 1 шектеусіз болса, онда
{\displaystyle {\begin{aligned}&z_{1}=z_{1}^{+}-z_{1}^{-}\\&z_{1}^{+}, \, z_{1}^{-}\geq 0\end{aligned}}}
Теңдіктен z 1 сызықты программалауда алып тастау мүмкін болды. Процесс толық мүмкін ауданға келгенде мынадай түрде жазылады
{\displaystyle \mathbf {A} \mathbf {x} =\mathbf {b}, \, x_{i}\geq 0}Бұл жердегі A қатардағы сан деп ойлаймыз. Бұл ешқандай кемшіліктергі әкелмейді немесе Ax >= b керек емес теңдеулерге, сызықтық программаның шешімі жоқ деген шешімге әкелуі мүмкін.
Сызықтық бағдарлама есебінің оңтайлы шешімдері көпбұрыштың бұрыштық нүетелерімен байланысты. Егер айнымалалар саны n=50, теңсіздіктер саны m=25 болса, онда базистік жоспарлар саны 10 14 болады. Сонда м және н үлкен сан болса, онда барлық негізге алынатын жоспарларды іріктей отырып, оңтайлыны табу өте көп есептеуді қажет етеді. Сондықтан бір негізге алынатын жоспардан екіншіге ауысуға мүмкіндік беретін әдіс болуға тиіс. Осындай әдіс симплекс әдісі деп аталады. Есептеулердің әрқайсысында осы функцияның өткен жоспардағы мәнімен салыстырғанда мақсатты функциядан кем немесе артық мәніне сәйкес келетін жаңа жоспар табылды. Есептеулерді оңтайлы жоспар алынғанға дейін жалғасады. Егер мәселенің оңтайлы шешімі болмаса, онда симплексті әдіс оны есептеу кезеңінде анықтауға мүмкіндік береді.
Алғашқы жоспар құру. Сызықтық бағдарлама есебі қойылған болсын. Төмендегі функцияның барынша аз мәнін табу қажет.
F=C 1 X 1 + C 2 X 2 +… +C n X n (5. 1)
мына шектеулерде
а 11 х 1 + а 21 х 2 + . . . +а 1n хn=В 1
а 21 х 1 + а 22 х 2 + . . . +а 2n хn=В 2
. . . (5. 2)
а m1 х 1 + а m2 х 2 + . . . +а mn х n =В m
мұнда,
х j >=0, (i=1, 2, …, m) . (5. 3)
Шектеу жүйесінің m бірлік векторлары болсын деп ұйғарсақ, онда ол алғашқы m векторлар болады. Осыдан (5. 1) - (5. 3) есепті алғашқы m векторларға сәйкес түрлендіріп жазамыз:
F=C 1 X 1 + C 2 X 2 +… +C n X n, (5. 4)
мына шектеулерде
X 1 +a 1 1 , m+1 X m+1 +a 1 1 , m+2 X m+2 +…+a 1 1. n x n =B 1 1
X 2 +a 2 , m+1 X m+1 +a 2 , m+2 X m+2 +…+a 1 2. n x n =B 1 2 (5. 5)
X m +a 1 m , m+1 X m+1 +a 1 m , m+2 X m+2 +…+a 1 m. n x n =B 1 m
х j >=0, j=1, 2, …, n. (5. 6)
Жүйені (5, 5) векторлық формада жазамыз:
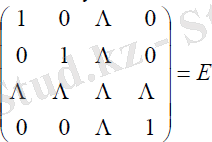
x 1 A 1 +x 2 A 2 +…+x m A m +x m+1 A m+1 +x n A n =B (5. 7)
А 1 , А 2 , . . . , А m векторлар - m өлшемді кеңістіктің сызықтық тәуелсіз бірлік векторлары. Сондықтан (5. 7) өрнекте базистік айнымалылар ретінде x 1, x 2, …, x m. Ал еркін айнымалылар ретінде x m+1, x m+2, …, x n таңдаймыз, оларды нөлге теңестіріп, базистік айнымалыларды анықтаймыз. Мұнда в і >=0 (і=1, 2, . . . m), ал А 1 , А 2 , . . . , А m бірлік векторлар екенін ескерсек, онда алғашқы жоспарды аламыз:
Х о =(х 1 =в 1 ; х 2 =в 2 ; . . . х m =в m ; х m+1 =0; . . . х n =0) (5. 8)
Жоғарыдағы (5. 7) -ден (5. 8) жоспарды ескерсек, төмендегі жіктеу шығады:
x 1 А 1 +х 2 А 2 + . . . + х m , А m = В, (5. 9)
мұнда А 1 , А 2 , . . . А m векторлар сызықтық тәуелсіз, демек, құрылған жоспар базис болып табылады.
1-анықтама. Еркін белгісіздердің нөл мағыналарына сәйкес келетін шектеулер жүйесінің (5. 2) шешімі базистік деп аталады.
Бастапқы негізге алынатын жоспарға (5. 9) сүйене отырып, екінші негізге алынатын жоспарды қалай құруға болатынын қарастырамыз. Базиске кірмейтін кейбір вектор үшін, мысалы А m+1 , жіктеудегі х і, m+1 коэффициенттердің ең болмағанда біреуі оң болады деп ұйғарамыз.
Х 1, m+1 А 1 +Х 2 , m+1 А 2 + . . . + Х m, m+1 А m =А m+1
Жүйенің оң жағы В бөлікті осы айнымалының оң коэффициенттеріне, яғни В і /а іm+1 бөлеміз. Сөйтіп, х m+1 векторы жоспар немесе жаңа базис болып табылады. Есептің m-нен асатын базисі болмайды, сондықтан қазіргі бар базистің біреуін алып тастаймыз. Ол үшін Q=min(в і /а i, m+1 ) . таңдаймыз. Осы ең кіші мәні бірінші жолда тұрсын, яғни Q 1 =min (в і /а 1, m+1 ) . Сонда жаңа базистік шешім аламыз Х=( x 2 , х з , . . . х m , х m+1 ) . Бұл базистен Х 1 алып тастау, ал базиске х m+1 енгізу қажет екенін білдіреді. Демек, негізге алынатын жаңа жоспарларды таңдау үшін, базистен шығарылатын және оның орнына базиске енгізілетін айнымалының векторын таңдау кажет.
Оңтайлылық талаптары. СБ есебінің базистік шешімі бар деп ұйғарамыз. Бұл жағдайда есептің математикалық формасы төмендегідей болады:
x 1 А 1+х2 А 2 + . . . + х m А m = В, (5. 10)
х 1 С 1 +х 2 С 2 + . . . + х m С m = Ғ, (5. 11)
мұнда барлық х j >=0, j=1, 2, . . . , n., ал Ғ-осы жоспарға сәйкес келетін функцияның мәні. Егер сызықтык функциядағы С j коэффициенті А j векторға сәйкес келсе, онда Ғ j -С j - оңтайлылық өлшемі немесе сызықтық функцияның бағасы деп аталады.
Оңтайлылық өлшемі бағдарламадан шығарылатын қызметтің құнының сомасына тең болады, одан жоспарға енгізілетін өнімнің бірлігінен түсетін кіріс алынып тасталады. Ғ j - мақсат функциясының коэффициенттерін шектеулердегі айнымалылардың коэффициенттеріне көбейтіндісінің қосындысына, яғни,
c j - мақсат функциясының белгісіздер коэффициенттері. Төмендегі теоремалар орын алады.
1-теорема. Егер кейбір А j векторы үшін төмендегі талап орындалса,
F j -C j >=0,
онда Х о жоспары функцияның максимумы үшін оңтайлы болып табылады.
2-теорема. Егер кейбір А j векторы үшін төмендегі талап орындалса, онда Х о жоспары функцияның минимумы үшін оңтайлы болып табылады. Демек, сызықтық функцияның максимумына сәйкес есептің жоспары оңтайлы болу үшін оның бағалары оң болуы қажетті әрі жеткілікті болады. Ал функцияның минимумы үшін оның бағалары теріс болуы қажетті әрі жеткілікті болады.
Сөйтіп, мәселені симплекс әдіспен шешу мына сызба бойынша жүргізіледі:
1) базистік шешім құрылады;
2) осы базистік шешім оңтайлылық шартына тексеріледі;
3) егер шарт орындалмаса, онда келесі базистік шешім құрылады да екінші тармаққа көшеді;
4) оңтайлылық талабы орындалғанға дейін есептеулер кайталанады.
Осы әдіспен есептеулер қайталана отырып, іріктеу нәтижесінде ең жақсы, яғни оңтайлы шешім табуға болатыны дәлелденген.
ІІІ. Практикалық бөлім
3. 1. Тапсырмаларды шешудің симплекстік әдістері
ЖП-дың төмендегі түрде жазылған есебін қарастырайық:

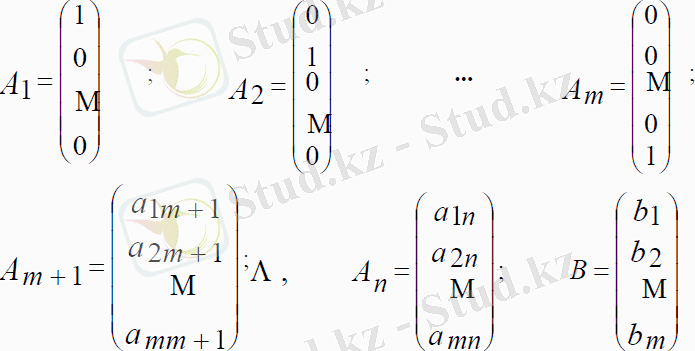
Көріп тұрғанымыздай,
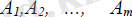 - векторлар жүйесі желілік тəуелсіз жəне матрица.
- векторлар жүйесі желілік тəуелсіз жəне матрица.
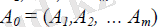
Бұл жағдайда, егер А1, А2, …, Аm - жүйесін бастапқы базис ретінде қабылдасақ, онда оған х=(х1, х2, …, хm, 0, . . . , 0) бастапқы тірек жоспары сəйкес келеді.
Мұнымен қатар, А0=Е болғандықтан, негізінде
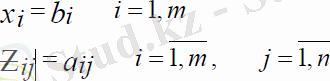
Осылайша, бастапқы тірек жоспары мына түрге ие: х=(b1, b2, …, bm, 0, . . . , 0) . Егер нольдік компоненттерді алып тастасақ, онда х = (b1, b2, …, bm) . Тірек жоспарын оңтайлылыққа зерттеуді, сонымен қатар одан кейінгі есептеу процедураларын симплексті деп аталатын төменде берілген кестелер түрінде жүргізген ыңғайлы (2-кесте) . Бұл кестедегі С0 бағанында желілік форманың базис векторындағыдай индекске ие белгісіздерінің коэффициенттері жазылады.

В бағанында бастапқы тірек жоспарының оң компоненттерін жазамыз. Осы бағанда есептеу нəтижесінде оңтайлы жоспардың оң компоненттері анықталады. Aj ( j =1, n ) векторларының бағандарында осы векторлардың ( Ζ ij ) базисі бойынша ажырау коэффициенті орналасады, берілген жағдайда Ζ ij = aij i =1, m , j =1, n . Осылайша, əуелгі кестенің бірінші m жолы есептің бастапқы деректері негізінде құрылады. Ал кестенің ( m+1 ) -ші жолының көрсеткіштері есептеліп шығарылады. В бағанындағы осы жолда желілік форманың берілген тірек жоспарына сəйкес келетін мəні жазылады, ал келесі Aj бағанында - Δ j = Ζ j − Сд , ( j =1, n ) мəні.
Шындығында да, мысалы, Δ1 -ді есептеп шығаралық:
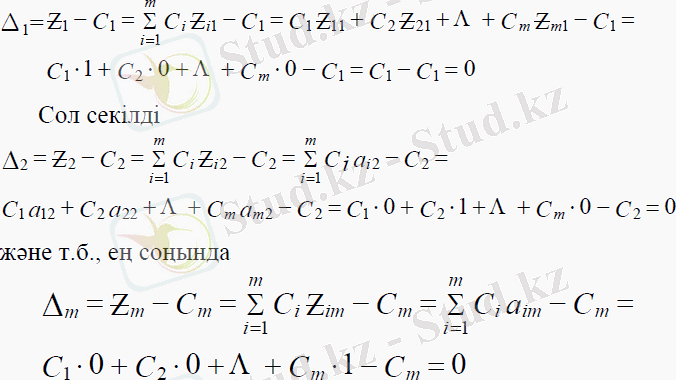
Симплексті кестенің бастапқы деректерін толтырғаннан кейін итеративті есептеу процесі басталады, ол төменде келтірілген бірнеше қадамнан тұрады.
1-қадам. Жоспарды оңтайлылыққа тексеру. Бұл үшін ( m+1 ) -ші жолдың элементтері қаралады - Δ j , j =1, n . Егер Δ j ≥ 0, j = 1, n болса, онда осы кестеде жазылған тірек жоспары оңтайлылық критерийіне сəйкес оңтайлы болып табылады. Есептеу процесі аяқталды. Егер Δ j<0 кейбір белгіленген j үшін болса, онда кестеде жазылған тірек жоспары оңтайлы емес болып табылады жəне оның жақсартылуы мүмкін, яғни желілік формасының мəні үлкен жаңа тірек жоспарын құруға болады. Жоғарыда айтылғандай, бір тірек жоспарынан екінші тірек жоспарына өту үшін бастапқы базис векторларының бірін шығарып, оның орнына басқа вектор енгізу керек. Сондықтан келесі қадамдар базиске енгізілетін жəне одан шығарылатын базистерді анықтаумен байланысты болады.
2-қадам. Базиске енгізілетін векторды анықтау. Жалпы алғанда, базиске енгізілетін вектор ретінде Аj векторларының ол үшін Δ j<0 болатын кез келген векторын алуға болады. Бірақ, оңтайлы жоспар алу процесін жылдамдату үшін базиске Аj- дің ол үшін Δ j, j min орын алатын векторын енгізген ыңғайлы. Δ j
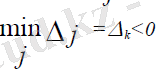 болсын делік. Бұл
Аk
векторының базиске
енгізілетінін білдіреді. Мұнда оған сəйкес келетін бағандыбағыттаушы деп атайды.
болсын делік. Бұл
Аk
векторының базиске
енгізілетінін білдіреді. Мұнда оған сəйкес келетін бағандыбағыттаушы деп атайды.
3-қадам. Базистен шығарылатын векторды анықтау. Базистен шығарылуы тиіс векторларды анықтау үшін
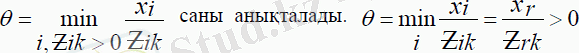 болсын делік. Бұл А
r
векторының базистен шығарылатынын білдіреді, ал кестенің
r-
ші жолын бағыттаушы деп атайды. Мұнда, атап өту қажет, егер Ζ
ik
≤ 0,
i
=1,
m
болса, онда есеп шешілмейді.
болсын делік. Бұл А
r
векторының базистен шығарылатынын білдіреді, ал кестенің
r-
ші жолын бағыттаушы деп атайды. Мұнда, атап өту қажет, егер Ζ
ik
≤ 0,
i
=1,
m
болса, онда есеп шешілмейді.
4-қадам. Симплексті кестенің Гаусс формулалары бойынша қайта құрылуы. Бұл қадамда бастапқы симплексті кестенің барлық элементтері Гаусс формулалары бойынша қайта құрылады. Мұнда жаңа тірек жоспарының компоненттері төмендегі формулалар бойынша анықталады:
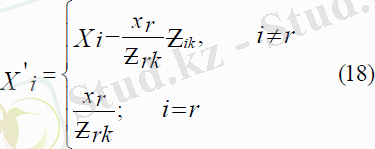
- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz