Анықталмаған интеграл: анықтама, қасиеттер, кесте және интегралдау әдістері (айнымалыны алмастыру және бөліктеп интегралдау)


Анықталмаған интеграл.
1. Алғашқы функция.
Көп жағдайда, әсірісе физика, механика және техника есептерінде берілген функцияның туындысы бойынша сол функцияның өзін табу амалдары қарастырылады. Сондықтан берілген функцияның туындысы
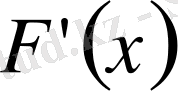 бойынша сол
бойынша сол
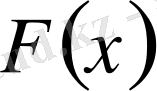 функциясының өзін табу тәсілдерін келтірейік.
функциясының өзін табу тәсілдерін келтірейік.
Анықтама 1. Егер
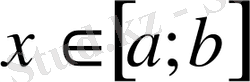 аралығында берілген
аралығында берілген
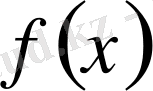 функциясы үщін
функциясы үщін
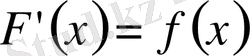 теңдігі орындалса, онда
теңдігі орындалса, онда
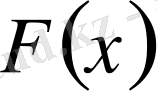 функциясы
функциясы
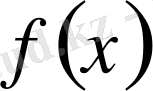 функциясының
функциясының
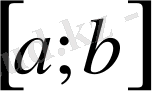 аралығындағы алғашқы функциясы деп аталады.
аралығындағы алғашқы функциясы деп аталады.
Мысал. Егер
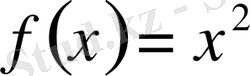 функциясы берілсе онда
функциясы берілсе онда
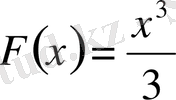 функциясы оның алғашқы функциясы болады.
функциясы оның алғашқы функциясы болады.
Шындығында да,
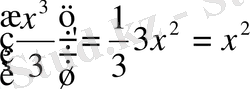
Бұл функцияның алғашқы функциясы бірмәнді болмайды, өйткені
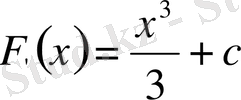 функциясы да С санының кез келген мәндерінде
функциясы да С санының кез келген мәндерінде
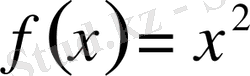 функциясының алғашқы функциясы болады, яғни
функциясының алғашқы функциясы болады, яғни
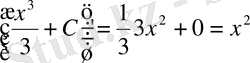
Сонымен, егер берілген
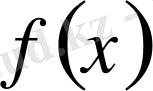 функциясының алғашқы функциясы
функциясының алғашқы функциясы
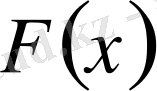 болса, онда бұдан өзгеше алғашқы функциялардың түрі
болса, онда бұдан өзгеше алғашқы функциялардың түрі
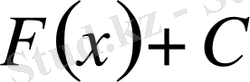 болады. Басқаша айтқанда, егер
болады. Басқаша айтқанда, егер
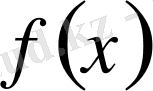 функциясының алғашқы функциялары бар болса, онда олардың айырымы тұрақты шамаға тең.
функциясының алғашқы функциялары бар болса, онда олардың айырымы тұрақты шамаға тең.
Анықтама 2. Егер
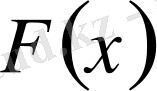 функциясы берілген
функциясы берілген
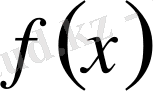 функциясының алғашқы функциясы болса, онда
функциясының алғашқы функциясы болса, онда
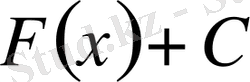 өрнегін
өрнегін
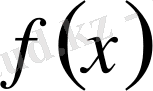 функциясының анықталмаған интегралы деп атайды және оны
функциясының анықталмаған интегралы деп атайды және оны
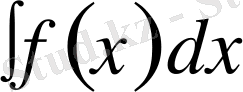 символымен белгілейді, яғни
символымен белгілейді, яғни
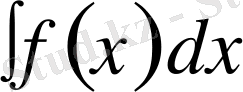

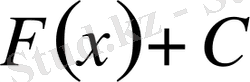
Мұндағы:
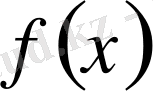 - интеграл астындағы функция;
- интеграл астындағы функция;
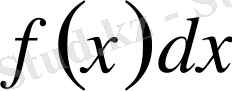 - интеграл астындағы өрнек;
- интеграл астындағы өрнек;
ал
 - интеграл белгісі деп аталады.
- интеграл белгісі деп аталады.
Берілген функцияның алғашқы функциясын табу интегралдау амалы деп аталады.
Геометриялық тұрғыдан анықталмаған интеграл жазықтықта бір-бірінен айырымы тұрақты шама болатындай қисықтар жиынын көрсетеді. Бұл қисықтарды интегралдық қисықтар деп атайды.
Анықталмаған интегралдың бар болу шартын келтірейік.
Теорема. Егер
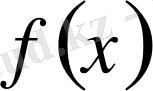 функциясы үзіліссіз болса, онда оның анықталмаған интегралы бар болады.
функциясы үзіліссіз болса, онда оның анықталмаған интегралы бар болады.
2. Анықталмаған интеграл және олардың қасиеттері, кестесі.
1 0 . Анықталмаған интегралдың туындысы интеграл астындағы функцияға тең болады, яғни
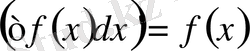
Дәлелдеуі. Интегралдың анықтамасы бойынша
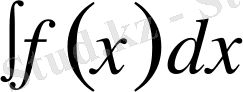

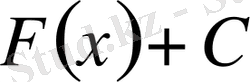 . Осы теңдіктің екі жағынан да туынды алсақ, онда
. Осы теңдіктің екі жағынан да туынды алсақ, онда
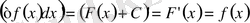
Келесі қасиеттерді де осылай дәлелдеуге болады.
2 0 . Анықталмаған интегралдың дифференциалы интеграл астындағы өрнекке тең болады, яғни
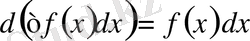
3
0
. Кез келген
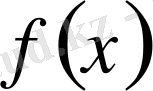 функциясы дифференциалының интегралы сол
функциясы дифференциалының интегралы сол
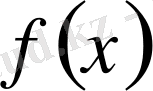 функциясы мен тұрақты С санының қосындысына тең болады, яғни
функциясы мен тұрақты С санының қосындысына тең болады, яғни
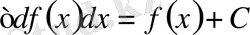
4 0 . Бірнеше функциялардың алгебралық қосындысының анықталмаған интегралы қосылғыштардан алынған анықталмаған интегралдардың алгебралық қосындысына тең, яғни
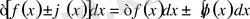
5
0
. Тұрақты санды интеграл белгісінің алдына шығаруға болады, яғни егер
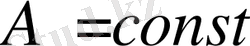 болса, онда
болса, онда
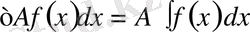
6
0
. Егер
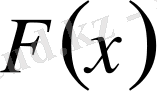 функциясы
функциясы
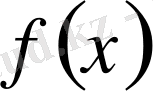 функцияның алғашқы функциясы болса, онда
функцияның алғашқы функциясы болса, онда
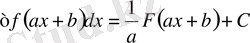
Мұндағы
 және
және
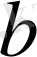 - тұрақты сандар
- тұрақты сандар
Интегралдау амалы дифференциалдау амалына кері болатынын ескерсек, онда интегралдар кестесін былай жазуға болады:
1.

2.
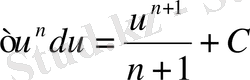 егер
егер
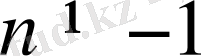
3.
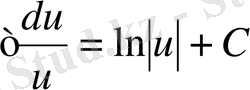
4.
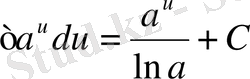
5.
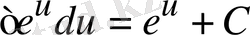
6.
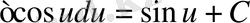
7.
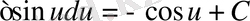
8.
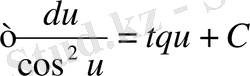
9.
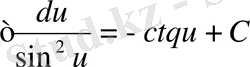
10.
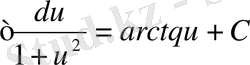
11.
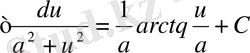
12.
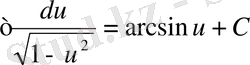
13.
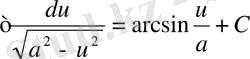
14.
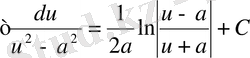
15.
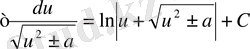
Бұл кестеге енген әрбір формуланың дұрыстығын дифференциалдау арқылы дәлелдеуге болады.
3. Айнымалыны алмастыру және бөліктеп интегралдау әдістері.
Берілген интегралды интегралдау әдістері интеграл астындағы функцияның берілуіне және интегралдар кестесінің қорына байланысты бірнеше түрге бөлінеді: тікелей интегралдау, айнымалыларды ауыстыру арқылы интегралдау; бөліктеп интегралдау. Осы тәсілдердің әрқайсысына жеке - жеке тоқталайық.
а) Тікелей интегралдау.
Көптеген функцияларды анықталмаған интегралдың қасиеттер мен интегралдар кестесіне сүйеніп тікелей интегралдауға болады. Тікелей интегралдау тәсіліне бірнеше мысалдар келтірейік.
б) айнымалыны алмастыру әдісі.
Көп жағдайларда интегралдағы
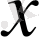 айнымалысының орнына басқа
айнымалысының орнына басқа
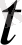 айнымалысын енгізіп, берілген
айнымалысын енгізіп, берілген
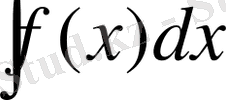 (1)
(1)
интегралын тікелей интегралданатын жаңа интегралдарға немесе кестелік интегралдардың біріне оңай келтіруге болады. Бұл әдісті айнымалыларды ауыстыру (немесе айнымалыны алмастыру) әдісі деп атайды.
Теорема.
Анықталмаған
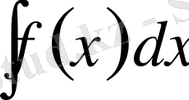 интегралындағы
интегралындағы
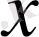 айнымалысының орнына
айнымалысының орнына
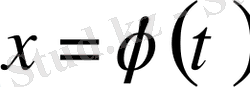 (2)
(2)
формуласы бойынша жаңа
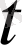 айнымалысын енгізейік (мұндағы
айнымалысын енгізейік (мұндағы
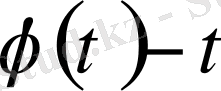 аргументінің бірсарынды, үзіліссіз және дифференциалданатын функциясы) . Сонда берілген анықталмаған интеграл үшін
аргументінің бірсарынды, үзіліссіз және дифференциалданатын функциясы) . Сонда берілген анықталмаған интеграл үшін
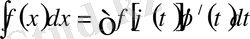 (3)
(3)
теңдігі орындалады.
Айнымалыларды ауыстыру әдісін ұтымды қолдану берілген айнымалыны қандай формула бойынша ауыстыруға байланысты. Яғни интегралдың берілуіне қарап, ауыстыру формуласын таңдап алу керек. Айнымалыларды ауыстыру арқылы интегралдау әдісіне бірнеше мысалдар келтірейік.
Дифференциалдары үзіліссіз
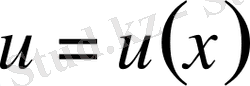 және
және
 функциялары берілсін.
функциялары берілсін.
Осы екі функция көбейтіндісінің дифференциалы
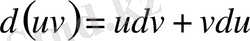
болады.
Бұл теңдіктің екі жағын да интегралдасақ,
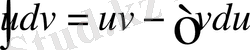 (4)
(4)
(4) формула
бөліктеп интегралдау формуласы
деп аталады. Бұл әдісті қолданғанда интеграл астындағы өрнекті екі көбейткіштің (
 және
және
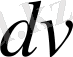 ) көбейтіндісі түрінде қарастыру керек. Сондықтан бөліктеп интегралдау әдісінің ұтымдылығы осы
) көбейтіндісі түрінде қарастыру керек. Сондықтан бөліктеп интегралдау әдісінің ұтымдылығы осы
 және
және
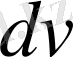 көбейткіштерін дұрыс таңдап алуға байланысты.
көбейткіштерін дұрыс таңдап алуға байланысты.
Көп жағдайларда бөліктеп интегралдау әдісі бойынша
 және
және
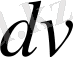 көбейткіштерін таңдап оларда төмендегі практикалық мәні бар интегралдарды ескерген жөн:
көбейткіштерін таңдап оларда төмендегі практикалық мәні бар интегралдарды ескерген жөн:
1. Егер
 ,
,
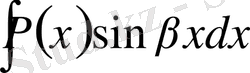 ,
,
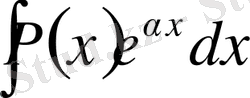 болса, онда
болса, онда
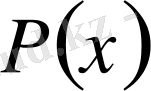 функциясын
функциясын
 , ал қалған
, ал қалған
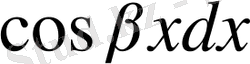 ,
,
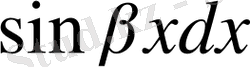 ,
,
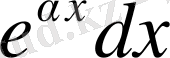 , өрнектерін
, өрнектерін
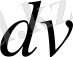 деп алу керек.
деп алу керек.
2. Егер
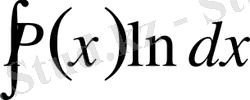 ,
,
 болса, онда
болса, онда
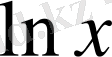 ,
,
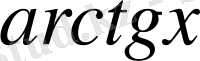 функцияларын
функцияларын
 , ал
, ал
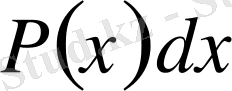 өрнегін
өрнегін
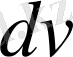 десек, берілген интегралдар оңай интегралданады. Енді осы әдістің қолдануына мысалдар келтірейік.
десек, берілген интегралдар оңай интегралданады. Енді осы әдістің қолдануына мысалдар келтірейік.
- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz