Кездейсоқ оқиғалар және ықтималдық теориясының негізгі теоремалары


КЕЗДЕЙСОҚ ОҚИҒАЛАР. ЫҚТИМАЛДАҚТАР ТЕОРИЯСЫНЫҢ НЕГІЗГІ ТЕОРЕМАЛАРЫ
1. Кездейсоқ оқиға. Оқиғалар классификациясы.
Ықтималдықтар теориясы кездейсоқ құбылыстардың заңдылығын зерттейтін математикалық ғылым болып саналады.
Ықтималдықтар теориясының негізгі ұғымдары - кездейсоқ оқиғалар және оқиғалардың ықтималдық ұғымы.
Оқиға деп, кейбір байқау, тәжірибе немесе эксперимент жасауда белгілі бір шарттардың жиынтығы орындалғанда пайда болатын немесе пайда болмайтын нәтижені айтады. Оқиғаларды латын алфавитінің алғашқы бас әріптерімен белгілейді:
A, B, C, …
Оқиға үш түрге бөлінеді: ақиқат, мүмкін емес және кездейсоқ.
Ақиқат оқиға деп, белгілі бір шарттар жиынтығы орындалғанда міндетті түрде пайда болатын оқиғаны айтады.
Мысалы, ойын сүйегін лақтырғанда 1-ден 6-ға дейінгі ұпайдың біреуінің түсуі ақиқат.
Мүмкін емес оқиға деп, белгілі бір шарттар тобы орындалғанда пайда болмайтын оқиғаны айтады.
Мысалға, ойын сүйегін бір рет лақтырғандағы түсетін ұпай санының 6-дан көп болуы мүмкін емес.
Кездейсоқ оқиға деп, белгілі бір шарттар тобы орындалғанда пайда болуы да, болмауы да мүмкін оқиғаны айтады.
Мысалы, “ойын сүйегін бір рет лақтырғанда 5 ұпай түсті” деген оқиға кездейсоқ оқиға болады.
Ықтималдықтар теориясы осы кездейсоқ оқиғаларды зерттейді.
Кездейсоқ оқиғалар: үйлесімді, үйлесімсіз, жалғыз ғана мүмкіндікті және тең мүмкінді болып бөлінеді.
Егер тәжірибе нәтижесінде бір оқиғаның пайда болуы қалған оқиғалардың пайда болуына кедергі жасамаса, онда мұндай оқиғаларды үйлесімді оқиғалар дейді.
Мысалы, жәшікте бірнеше зауытта жасалынған тек жоғары сортты бөлшектер бар. Таңдамай, қалай болса солай алынған бөлшектің: а) жоғары сортты болуы; б) белгілі бір зауытта жасалынған болуы - үйлесімді оқиғалар.
Егер тәжірибеде бір оқиғаның пайда болуы қалғандарының пайда болуына кедергі болса, ондай оқиғаларды үйлесімсіз оқиғалар дейді.
Мысалы, теңгені бір рет тастағанда “герб” түсуі “цифр” түсуіне мүмкіндік бермейді (кедергі жасайды) . Сондықтан “герб түсті” және “цифр түсті” деген оқиғалар өзара үйлесімсіз.
Егер тәжірибе нәтижесінде пайда болған оқиға ақиқат оқиға болса, онда ол жалғыз мүмкіндікті оқиға деп аталынады.
Теңгені бір рет тастағанда міндетті түрде жоғарыда аталынған екі оқиғаның бірі пайда болады. Сондықтан бұл оқиғалар жалғыз ғана мүмкіндікті.
Егер оқиғалардың пайда болу мүмкіндіктері бірдей деп есептелінсе, ондай оқиғаларды ТЕҢ МҮМКІНДІ оқиғалар дейді.
Ойын сүйегін лақтырғанда 1-ден 6-ға дейінгі кез келген ұпайдың пайда болуы ТЕҢ МҮМКІНДІКТІ ОҚИҒА. Себебі, ойын сүйегі біртекті материалдан жасалынған, цифрлар саны оның әрбір жағының салмағына әсер етпейтін, дұрыс көпбұрыш деп есептелінеді.
2. Ықтималдық. Шартты ықтималдық.
Ықтималдық ұғымы ықтималдықтар теориясының негізгі ұғымдарының бірі екендігі айтылды. Ықтималдықтың бірнеше анықтамасы бар, соның бірін беру үшін мынадай мысал қарастырылады:
Жәшікте мұқият араластырылған 7 шар бар болсын, оның үшеуі қызыл, екеуі ақ, қалған екеуі көк. Жәшіктен қалай болса солай бір шар алынған. Алынған шардың түрлі түсті (қызыл не көк) болу мүмкіндігі (оқиға А), оның ақ шар болу мүмкіндігінен (оқиға В) үлкен. Біз ынта білдіріп отырған оқиғаның (А) пайда болатын жағдайларын А оқиғасына қолайлы жағдайлар (оқиғалар) дейді. Қарастырылып отырған мысалда А оқиғасының пайда болуына қолайлы жағдайлар саны бесеу, ал барлық мүмкін болатын элементар жағдайлар саны жетеу.
АНЫҚТАМА. А оқиғасының ықтималдығы Р(А) деп, осы оқиғаға қолайлы жағдайлар санының (m) барлық санына (n) қатынасын айтады, яғни
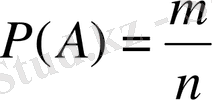
Бұл анықтаманы ықтималдықтың классикалық анықтамасы дейді.
Анықтаманы алдыңғы қаралған мысалға қолдансақ, онда m=5, ал n=7 болады да, түрлі түсті шар алу ықтималдығы
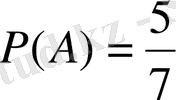 болады.
болады.
Классикалық анықтама бойынша анықталған ықтималдықтың мынадай қасиеттері бар:
1. Ақиқат оқиғаның ықтималдығы бірге тең, яғни P(A) =1, егер А -ақиқат оқиға болса. Себебі, ақиқат оқиғалардың пайда болуына барлық жағдайлар қолайлы.
2. Мүмкін емес оқиғаның ықтималдығы нөлге тең, P(A) =0, егер А -мүмкін емес оқиға болса. Расында мүмкін емес оқиғаның пайда болуына ешбір жағдай қолайлы емес.
3. Қандай да болмасын оқиғаның ықтималдығы нөл мен бірдің арасында жатқан нақты сан,
0≤ P(A) ≤1.
А -кездейсоқ оқиға болса, онда А -ға қолайлы жағдайлар саны m, барлық жағдайлар саны n -нен кіші, яғни 0≤m≤n осыдан 0≤P(A) ≤1 шығады.
Мысал.
Бір колода құратын 36 карта мұқият араластырылған, яғни әрбір картаның орналасу мүмкіндігі тең ықтималды.
1) Колодадан алынған бір картаның тұз болу;
2) бірінен соң бірі алынған екі картаның екуі де тұз болу ықтималдығын табу керек.
Шешуі. 1) T 1 ( түз пайда болуы) оқиғасына қолайлы элементар жағдайлар саны m=4, ал барлық тең мүмкінді жағдайлар саны n=36, сондықтан іздеп отырған ықтималдық
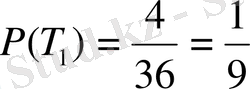
2)
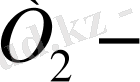 бірінен соң бірі алынған екі картаның екуі де тұз болуы
бірінен соң бірі алынған екі картаның екуі де тұз болуы
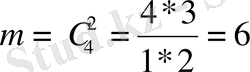 , ал
, ал
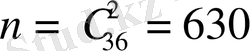 Equation. 3
Equation. 3
болады да, ізделініп отырған ықтималдық
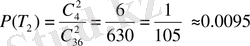
Бұл есепті шығаруда
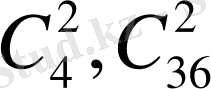 , сияқты шартты белгілер қолданылды, ол белгілер терулер санын көрсетеді. Терулер ұғымы комбинаторика ұғымына жатады. Осы мәселелерді қарастырайық.
, сияқты шартты белгілер қолданылды, ол белгілер терулер санын көрсетеді. Терулер ұғымы комбинаторика ұғымына жатады. Осы мәселелерді қарастырайық.
А және В оқиғалары тәуелді болсын. Тәуелді оқиғаларының анықтамасынан, бір оқиғаның ықтималдығы екіншісінің пайда болғанына, немесе болмағанына байланысты екенін білеміз. Сондықтан, А оқиғасының ықтималдығын анықтау үшін В оқиғасы пайда болды ма, болмады ма, соны білген өте маңызды. Мұндайда А оқиғасының ықтималдығы В оқиғасының пайда болғандығы шартты ықтималдығы болады.
Анықтама. А оқиғасының В оқиғасы пайда болғандағы ықтималдығы шартты ықтималдық деп аталады да
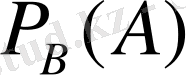 , немесе
, немесе
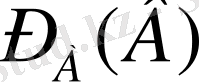 деп белгіленеді.
деп белгіленеді.
3. Ықтималдақтарды қосу және көбейту теоремалары.
1-теорема. Үйлесімсіз екі А және В оқиғалар қосындысының ықтималдығы олардың ықтималдықтарының қосындысына тең, яғни
P(A+B) =P(A) +P(B) .
Салдар. Егер
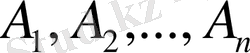 қос-қостан үйлесімсіз оқиғалар болса, онда бұл оқиғалардың қосындысының ықтималдығы әрбіреуінің ықтималдықтарының қосындысына тең болады, яғни
қос-қостан үйлесімсіз оқиғалар болса, онда бұл оқиғалардың қосындысының ықтималдығы әрбіреуінің ықтималдықтарының қосындысына тең болады, яғни
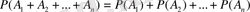 .
.
- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz