Кездейсоқ шамалардың сандық сипаттамалары: үлестірім, математикалық үміт, дисперсия және орташа квадраттық ауытқу


КЕЗДЕЙСОҚ ШАМАЛАРДЫҢ САҢДЫҚ
СИПАТТАМАЛАРЫ
1. Кездейсоқ шамалар және олардың үлестерім заңдары.
Практикада бірқатар мәндер қабылдайтын шамалар жиі кездеседі, бірақ олардың қарастырылып отырған тәжірибеге, құбылыста, бақылауда қандай мән алатынын алдын ала дәлдеп айту мүмкін емес. Мысалға, жақын күндердің бірінде Алматыда туатын ұл балалар саны әртүрлі болуы мүмкін. Бұл сан нөлге, бірге, екіге және тағы басқа шектеулі n санына тең болуы мүмкін. Осыған ұқсас шалаларға: бір партиядағы ақаулы детальдар саны: бір участіктен жиналған қант қызылшасының тамыр жемісінің салмағы; артиллерия снарядының ұшу алыстығы және т. б. жатады. Мұндай шараларды кездейсоқ шамалар деп атайды. Олар тәжірибенің барлық ықтимал нәтижелерін сандық жағынан сипаттайды. Сонымен, кездейсоқ шама деп сандық мән қабылдайтын, бірақ қандай мән қабылдайтынын алдын ала болжап айту мүмкін болмайтын шамаларды айтады.
Кездейсоқ шамалар латын алфавитінің бас әріптерімен X, Y, Z…, ал оларды қабылдайтын мәндері кіші әріптерімен х, у, z, . . . белгіленеді.
Кейзейсоқ шамалар қабылдайтын мәндеріне қарай екі топқа бөлінеді: дискретті және үзіліссіз кездейсоқ шамалар.
Егер кездейсоқ шаманың қабылдайтын мәндері біріне-бірі байланыссыз, шектелген бүтін сандар немесе сандар тізбегі түрінде жазылса, онда мұндай кездейсоқ шаманы дискретті дейді.
2. Үзіліссіз және дискреттік кездейсоқ шамалар
Анықтама. Дискреттік /үзілісті/ деп, белгілі бір ықтималдығы бар жекелеген, бөлектенген мұмкіндіктері бар мәндерді қабылдайтын кездейсоқ шамаларды айтады.
Дискретті кездейсоқ шамалардың мұмкін болатын мәндерінің саны шектіде, шексізде болуы мұмкін.
Анықтама.
Үздіксіз деп, кезкелген шекті немесе шексіз аралықта, оның барлық мәндерін
қабылдайтын кездейсоқ шамаларды айтады.
Дискретті кездейсоқ шаманы анықтау үшін әдетте кесте құрады. Мұндай кестеде екі жол болады. Оның бірінші жолында кездейсоқ ⁄Х⁄ шаманың қабылдайтын мәндері х 1 , х 2 , … х n , ал екінші жолында сол мәндерді қабылдау ықтималдықтары ⁄Р⁄ жазылады.
Мұндай кестені кездейсоқ шаманың үлестірім кестесі немесе үлестіру заңы деп атайды.
Кездейсоқ шаманың ⁄Х⁄ мәндері өзара үйлесімсіз жалғыз ғана мүмкіндікті оқиғалар болғандықтан, олар толық топ құрайды. Сондықтан олардың ықтималдықтарының қосындысы 1-ге тең:
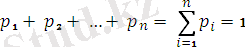
3. Математикалық үміт, дисперсия және олардың қасиеттері.
Кейбір жағдайларда кездейсоқ шаманың үлестіру заңы белгісіз болуы мүмкін, онда осы шамаларды анықтау мақсаты мен сандық сипаттамалары беріледі. Солардың бірі - математикалық үміт М(Х) .
Дискретті кездейсоқ шаманың математикалық үміті деп оның барлық қабылдайтын мәндерімен сол мәндерге сәйкес ықтималдықтарының көбейтінділерінің қосындысын айтады, яғни
Математикалық үміт кездейсоқ шаманың орта мәніне тең болады.
Егер кездейсоқ шама Х-қабылдайтын мәндері х 1 , х 2 , … х n, …, ал оларға сәйкес ықтималдықтары р 1 , р 2 , … р n , …, болса және i қатары абсолютті жинақты болса, онда осы қатардың қосындысын кездейсоқ шаманың математикалық үміті дейді.
Математикалық үміттің қасиеттері:
1. Түрақты шаманың математикалық үміті сол шаманың өзіне тең.
Яғни М(С) = С, С - тұрақты шама;
2. Түрақты санды математикалық үміт таңбасының алдына шығарып жазуға болады:
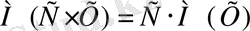
3. Екі тәуелсіз кездейсоқ шаманың көбейтіндісінің математикалық үміті, олардың математикалық үміттерінің көбейтінділеріне тең:
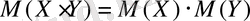
Салдар. Бірнеше тәуелсіз кездейсоқ шаманың көбейтіндісінің математикалық үміті, олардың математикалық үміттерінің көбейтінділеріне тең.
Мысалы,

4. Екі кездейсоқ шаманың алгебралық қосындысының математикалық үміті олардың математикалық үміттерінің алгебралық қосындысына тең:
М(Х±Y) = М(Х) ± М(Y) .
Салдар. Бірнеше кездейсоқ шамалардың алгебралық қосындысының математикалық үміті олардың математикалық үміттерінің алгебралық қосындысына тең.
1-мысал. Үлестіру заңы белгілі (Х) кездейсоқ шаманың математикалық үмітін табайық:
Шешуі:
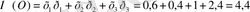
Теорема.
п-рет тәжірибе жүргізгенде А оқиғасының пайда болу санының математикалық үміті, тәжірибенің санына, оның әрбір тәжірибеде пайда болу ықтималдығын қөбейткенге тең:
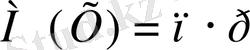
Мысал.
Мылтықтан атылған оқтын нысанаға дәл тию ықтималдығы Р=0, 6.
Егер мылтықтан 10 рет оқ атылған болса, жалпы алғанда нысанаға дәл тию санының математикалық үмітін табыңыз.
Шешуі.
Әрбір атылған оқтың нысанаға дәл тиюі, басқа атылған оқтардың нәтижесіне байланыссыз, сондықтан қарастырылып отырған оқиғалар тәуелсіз. Бұл жағдайда ізделіп отырған математикалық үмітті былай табамыз
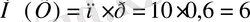
Кездейсоқ шаманың математикалық үміті сол шаманың, жалпы алғанда, негізгі бір сипаттамасы екендігін көрдік. Енді өзінеңөзі келіп кездейсоқ шаманың мәні есебінде математикалық ұмітті қабылдағанда жіберген қәтені бағалау мәселесі шығады. Физикада математикалық үміттін аналогиясы дененің ауырлық центірінің координаттары, ал ауырлық центрден ауытқу мәселелері инерциал моменттері арқылы шешіледі. Кездейсоқ шаманың мәндері оның математикалық үміттінең ауытқитындығы түсінікті. Міне, осы ауытқуды бағалау үшін дисперсия (шашырау) үғымы еңгізіледі. Х кездейсоқ шаманың дисперсиясын Д(Х) таңбасымен белгілейік.
Х кездейсоқ шама және М(Х) оның математикалық үміті болсын. ХМ(Х) айырымын жаңа кездейсоқ шама ретінде қарастырайық.
ХМ(Х) айырымын кездейсоқ шаманың оның математикалық үмітінен ауытқуы деп атайды.
Теорема.
Ауытқудың математикалық үміті нөлге тең
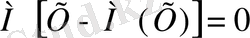
Дәлелдеу.
Математикалық үміттің қасиеттерін еске алсақ және математикалық үміттің
[ М(Х) ] түрақты шама екенін ескерсек, былай болады
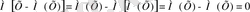
Анықтама. Х кездейсоқ шамасының ДИСПЕРСИЯСЫ (шашырау) деп, кездейсоқ шаманың математикалық үміттен ауытқуының квадратының математикалық үмітін айтады:
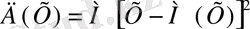
Анықтама.
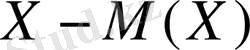 айырымын кездейсоқ шаманың оның математикалық күтімінен
ауытқу
деп атайды.
айырымын кездейсоқ шаманың оның математикалық күтімінен
ауытқу
деп атайды.
Теорема. Ауытқудың математикалық күтімі нольге тең, яғни
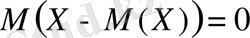 .
.
Дәлелдеуі. Математикалық күтімнің қасиеттерін еске алсақ және
 екенін ескерсек, мынаны аламыз
екенін ескерсек, мынаны аламыз
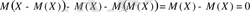 .
.
Дисперсияның қасиеттері.
1 0 . Тұрақтының дисперсиясы 0-ге тең, яғни
 (16)
(16)
Дәлелдеуі.
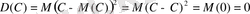
2 0 . Тұрақтыны дисперсиясы таңбасының сыртына квадрат дәрежелеп шығаруға болады, яғни
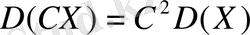 (17)
(17)
Дәлелдеуі.
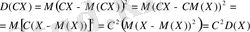
3 0 . Екі тәуелсіз кездейсоқ шама қосындысының (айырымының) дисперсиясы олардың дисперсияларының қосындысына тең.
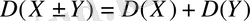 (18)
(18)
Дәлелдеуі.
а)
 екенін дәлелдейік.
екенін дәлелдейік.

(мұндағы
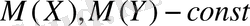 дәлеледенген теорема бойынша
дәлеледенген теорема бойынша
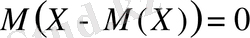 ,
,
 ) =
) =
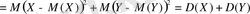 .
.
ә) Енді
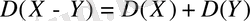 болатынын дәлелдейік.
болатынын дәлелдейік.

Салдар 1
. Кездейсоқ шама мәніне тұрақты
 -ны қосқаннан (азайтқаннан) диперсия мәні өзгермейді, яғни
-ны қосқаннан (азайтқаннан) диперсия мәні өзгермейді, яғни
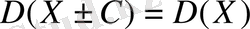 (20)
(20)
- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz