Кездейсоқ шамалардың үлестірім заңдары: биномдық, пуассондық, бірқалыпты, көрсеткіштік және нормальдық үлестірімдер

Пән: Математика, Геометрия
Жұмыс түрі: Материал
Тегін: Антиплагиат
Көлемі: 4 бет
Таңдаулыға:

КЕЗДЕЙСОҚ ШАМАЛАРДЫҢ ҮЛЕСТЕРІМ ЗАНДАРЫ

Биномдық үлестірім заңы.

Анықтама. Егер

\[\mathbf{\nabla}\times\]

- дискретті кездейсоқ шамасының үлестірім таблицасы берілсе және сол таблицадағы сәйкес ықтималдық мына формула арқылы анықталса, яғни

\[P_{k}\,=\,p(x=x_{k}\,)=C_{n}^{k}\,p^{k}q^{n-k}\]

\[p\gg0\]

\[q=1-p\]

болса, онда

\[\mathbf{X}\]

кездейсоқ шамасын Бернулли заңы бойынша үлестірімді деп атайды.

Мұндай үлестірімді басқаша биномдық үлестірім деп атайды.

Бернулли заңына

\[\mathbf{\nabla}/\hbar\]

оқиғасының бір-біріне тәуелсіз жүргізілетін тәжірибелердегі пайда болу саны бағынады, мұнда

\[{\mathcal{N}}\]

- тәжірибе саны,

\[P(A)=p\]

\[q=P({\overline{{A}}})=1-\ P(A)=1-p\]

\[C_{n}^{k}\]

- терулер саны.

Сонымен мынадай есепті шығарайық.

\[\mathbf{X}\]

- кездейсоқ шамасының үлестірім заңын табу керек, яғни

\[\mathbf{\nabla}\times\]

- тің мүмкін мәндерін және сол мәндерді қабылдау ықтималдығын табу керек.

\[{\mathcal{N}}\]

рет тәжірибе

шамасының үлестірім кестесі берілсе және сол кестеге сәйкес ықтималдық мына формула арқылы анықталса, жасағанда

\[\mathbf{\nabla}\lambda\]

оқиғасы бір рет те пайда болмауы мүмкін, бір рет, 2 рет, . . . ,

\[{\cal J}_{\bar{\cal L}}\]

рет пайда болуы мүмкін. Сондықтан

\[\mathbf{\nabla}\times\]

- тің мүмкін мәндері мынадай болады:

\[x_{1}=0\]

\[x_{2}=1\]

\[x_{3}=2\]

, . . . ,

\[X_{n+1}\implies\gamma\bar{l}\]

Бұл мәндердің ықтималдықтарын табу үшін Бернулли формуласын қолдануға болады.

\[P_{n}(k)=C_{n}^{k}\,p^{k}q^{n-k}\]

Осы формула іздеп отырған үлестірімдік заңының аналитикалық өрнегі болып есептеледі.

Биномдық үлестірім заңын таблица арқылы көрсетүге болады.

\[\mathbf{\nabla}\times\]

. . .

\[{\mathcal{N}}\]

. . .

\[{\mathcal{N}}\]

\[P_{n}(x)\]

\[C_{n}^{0}p^{0}q^{n}\]

\[C_{n}^{1}p^{1}q^{n-1}\]

. . .: . . .

\[C_{n}^{k}p^{0}q^{n-k}\]

. . .: . . .

\[C_{n}^{n}\,p^{n}q^{n-1}\]

Пуассондық үлестірім заңы.

Егер әрбір тәжірибеде

\[\mathbf{\nabla}\lambda\]

оқиғасының пайда болу ықтималдығы тұрақты

\[\ D\]

-ға тең тәуелсіз

\[{\cal J}_{\bar{\cal L}}\]

- тәжірибе жүргізілгенде

\[\mathbf{\nabla}\lambda\]

оқиғасының дәл

\[{\mathcal{N}}\]

рет пайда болу ықтималдығын есептеу үшін Бернулли формуласы қолданылады. Егер тәжірибе саны

\[{\cal J}_{\bar{\cal L}}\]

өте үлкен болса, онда Лапластың жуықтап есептеу формуласы қолданылады. Ал егер

\[\mathbf{\nabla}/\hbar\]

оқиғасының пайда болу ықтималдығы

\[\ D\]

өте аз болса, онда Пуассонның жуықтап есептеу формуласын қолдану керек.

Сонымен, саны өте көп

\[{\cal J}_{\bar{\cal L}}\]

тәжірибе жүргізгенде, әрбір тәжірибедегі

\[\mathbf{\nabla}\lambda\]

оқиғасының пайда болу ықтималдығы

\[{\mathcal{D}}\]

өте аз

және оқиға

\[{\mathcal{N}}\]

рет пайда болса

\[\bigl(n p=\,\lambda-c o n s t\bigr)\]

мына

\[P_{n}(k)={\frac{\lambda^{k}}{k!}}\cdot e^{-i}\]

Пуассонның жуықтап есептеу формуласы арқылы кездейсоқ

\[\mathbf{\nabla}\times\]

шамасының үлестірім заңын табуға пайдаланады.

Пуассон формуласы - өте сирек пайда болатын оқиғаларға тән заң және сондай жағдайларды сипаттайтын математикалық модель. Ықтималдықтардың Пуассондық үлестірім биномдық үлестірім сияқты кестемен және график арқылы да көрсетуге болады.

Бірқалыпты үлестірім заңы. Көрсеткіштік үлестірім заңы және қалыпты үлестірім заңы.

Анықтама .

\[\left(-{\frac{\Omega}{\kappa}}\ \mathbf{\Sigma}_{,}+\infty\right)\]

аралығынан мән қабылдайтын және ықтималдықтар тығыздығы

\[f(x)={\frac{1}{s\;\sqrt{2\pi}}}e^{\frac{.(x-a)^{2}}{2\sigma^{2}}}\]

(22) .

формуласымен өрнектелген үздіксіз кездейсоқ шаманың үлестірім ықтималдығын нормалдық деп атайды. Формуладағы

\[a,\sigma\]

параметрлер. Нормальдық үлестірімді жазу үшін осы екі параметрді білу жеткілікті

\[{\mathcal Q}\,\]

- математикалық күтім,

\[{\mathcal{O}}\]

- нормальдық үлестірімнің орташа квадраттық ауытқуы. Бұл параметрлердің ықтималдық мағынасын көрсетелік.

Үздіксіз кездейсоқ шама

\[\mathbf{X}\]

- тің математикалық күтімінің формуласы бойынша

Анықтама . Егер Хкездейсоқ шамасы (а, в) аралығында мәндер қабылдаса және үлестіру тығыздығы сол кезінде тұрақты шамаға тең болса, онда кездейсоқ шама бірқалыпты үлестірілген деп аталады.

Сонымен

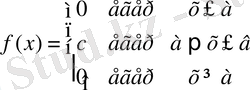
теңдігімен анықталса, онда Хкездейсоқ шамасы (а, в) аралығында бірқалыпты үлестірілген деп аталады. Үлестіру тығыздығының қасиеті бойынша

\[\textstyle\bigwedge_{a}d x=1\]

Осыдан

\[\tilde{n}(\hat{a}-\hat{a})=1;\]

\[c={\frac{1}{b-a}}\]

Сондықтан,

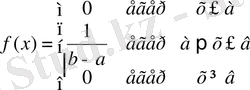
Бұл үлестірім заңдылығы үшін

\[\hat{I}\ \left(\tilde{O}\right)=\frac{\hat{a}+\hat{a}}{2};\tilde{A}\left(\tilde{O}\right)=\frac{\left(\hat{a}-\hat{a}\right)^{2}}{12}\]

Бірқалыпты үлестіру заңына ие кездейсоқ шаманың үлестіру функциясы F(x) келесі түрде жазылады:

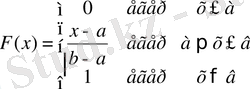
\[F(x)=_{\;a}^{x}f(x)d x={\frac{^x}{a}}{\binom{d x}{b-\ a}}={\frac{x-\ a}{b-a}}\]

Анықтама . Егер Х -кездейсоқ шамасы мына үлестірім тығыздығы

\[f(x)=\frac{\mathrm{{l}}\,\lambda\,e^{-\lambda x}}{\bigl[}\underbrace{{a}{\hat{a}}{\hat{a}}\bigr]}_{{\ }}\,\ {\tilde{a}}{\tilde{a}}{\tilde{a}}\ _{\dagger}\ 9\,0\]

арқылы берілсе, онда ол көрсеткіштік үлестірім заңымен берілген дейді, мұндағы

\[\lambda\ \cap\ 0\]

параметр.

Бұл жағдайда

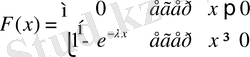
\[F(x)=\sum_{x.}^{x}\!\!f(x)d x=\underline{{{\bigcup_{c v}^{x}}}}e^{-\iota x}d x=1-e^{-\dot{x}x}\]

; сонда интегралдық функциясы болады:

Бұл үлестірімнің сандық сипаттамалары:

\[I\setminus(\emptyset)={\frac{1}{\lambda}},\]

\[\vec{A}\left(\vec{O}\right)=\frac{1}{\lambda^{2}},\]

\[s\ ({\hat{O}})={\frac{1}{\lambda}}\]

Кездейсоқ шаманың

\[[a,b]\]

аралығынан мән қабылдау ықтималдығы

\[{\cal D}(\hat{a}\ \Xi\ \tilde{O}\ \hat{a}=-\,\hat{a}^{-l\,\hat{a}}-\hat{a}^{-\hat{a}^{-\hat{a}}}\]

Қөрсеткіштің үлестіру заңында кездейсоқ Х шамасының үлкен мәндерінің ықтималдығы аз болады.

Анықтама . Егер Х -кездейсоқ шамасы мына үлестірім тығыздығы

\[f(x)={\frac{1}{s~\times{\sqrt{2\pi}}}}\cdot e^{-{\frac{(x-a)^{2}}{2\sigma^{2}}}}\]

(

\[{\mathcal{Q}}\]

)

арқылы берілсе, онда ол нормальды ( қалыпты) үлестірім заңымен берілген дейді.

(

\[{\mathcal{Q}}\]

) формуласынаң нормальдық үлестірімнің екі параметр арқылы анықталатынын байкаймыз:

\[\mathbf{\hat{d}}\]

және

\[\textstyle{\mathcal{O}}\]

. Нормалдық үлестірімді жазу үшін осы екі параметрді білу жеткілікті.

Математикалық күтімі (үміті)

\[I\setminus(O)={\dot{a}},\]

яғни нормальдық үлестірімнің математикалық күтімі оның параметрі

\[{\hat{a}}-\]

ға тең.

Дисперсия

\[{\tilde{A}}({\tilde{O}})=\sigma^{2}\]

, ал

\[s\;(\;\tilde{O})=\sqrt{\dot{A}\left(\,\tilde{O}\right)}=\sqrt{s\;^{2}}=\sigma\]

Сонымен нормальдық үлестірімнің орташа квадраттық ауытқуы оның параметрі

\[\textstyle{\mathcal{O}}\]

ға тең.

Нормальдық кездейсоқ шаманың берілген интервалға

дәл келу ықтималдығы.

Бізге белгілі, егер Х кездейсоқ шамасы үлестірім тығыздығы

\[f(\,x\,)\]

- арқылы берілсе, онда Хтін

\[(a:\beta)\]

аралығында жататын мәндерді қабылдау ықтималдығы төмендегідей болады:

\[D(a\ \textup{p}\tilde{O}\ \tilde{O}\ \tilde{o}\ \tilde{o}=\frac{1}{s\ \cdot{\sqrt{2\pi}}\ }\operatorname{_{a}}^{\beta}\operatorname{_{\tilde{U}}}^{-{\frac{(\tilde{o}-\tilde{a})^{2}}{2s^{2}}}}d x\]

Егер
\[z={\frac{\partial-a}{\sigma}}\]
ауыстуруын енгізсек, формула мына түрге келеді:

\[P(a\ \textup{p}\bar{O}\ \mathbb{O}\ 0\ b\ )=\partial({\frac{b-{\hat{a}}}{s}})-{\bar{O}}({\frac{a-{\hat{a}}}{\sigma}})\]

\[{\big.}{\big(}\cdot{\big)}\]

Мұндағы :

\[{\hat{a}}-\]
нормаль үлестрімді кездейсоқ шаманың математикалық күтімі;

\[{\boldsymbol{\sigma}}-\]

оның орташа квдраттық ауытқуы; ал

\[\hat{O}(\tilde{O})={\frac{1}{\sqrt{2\pi}}}\sum_{0}^{\tilde{o}}\frac{\stackrel{\leftarrow}{\cal Z}^{2}}{\vartheta}(\frac{\stackrel{\leftarrow}{\cal Z}^{2}}{\vartheta})\]

... жалғасы

Сіз бұл жұмысты біздің қосымшамыз арқылы толығымен тегін көре аласыз.