МАТРИЦАЛАР ЖӘНЕ АНЫҚТАУЫШТАР

Пән: Математика, Геометрия
Жұмыс түрі: Материал
Тегін: Антиплагиат
Көлемі: 6 бет
Таңдаулыға:

МАТРИЦАЛАР ЖӘНЕ АНЫҚТАУЫШТАР .

1. Матрицалар және олардың түрлері.

Анықтама. m*n-ретті матрица деп, m-жатық және n-тік жолдардан анықталған тік бұрышты кестені айтады, ол мына түрде белгіленеді:

A= 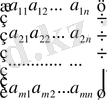(1) Немесе ; ;

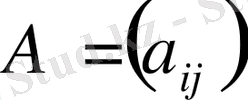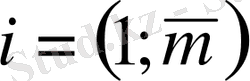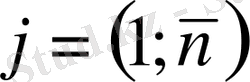
Мұндағы 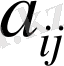-матрицаның элементтері деп аталады, бірінші индекс і матрицаның жатық жолының, ал екінші индекс j-тік жолының нөмерін анықтайды. Матрицалар латын алфавитінің бас әріптерімен (A, B, C . . . ) белгіленеді, ал матрицалардың элементтері - кіші әріптерімен: , .

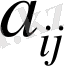Матрицаның дербес түрлері .

Егер матрицаның жатық жолының саны тік жолының санына тең болса, яғни: m=n, онда ол матрица квадратты (квадрат) матрица деп аталады, яғни:

A= 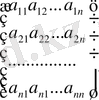(2)

Бұл жағдайда А матрица n-ші ретті матрица деп аталады.

Квадратты матрицаның 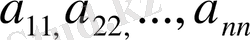элементтері оның бас диагоналы, ал 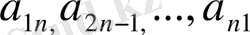элементтері қосалқы диагоналы деп аталады.

Егер матрицаның барлық элементтері нөлге тең болса, онда ол матрица нөл матрица деп аталады және ол 0 символымен белгіленеді:

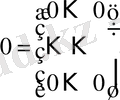
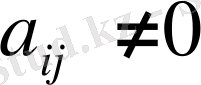Егер матрицаның бас диагоналының элементтерінен өзге элементтері нөлге тең болса: егер егер

Онда ол матрица диагоналды матрица деп аталады.

Егер диагоналды матрицаның барлық элементтері бірге тең болса: 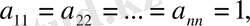онда ол бірлік матрица деп аталады және ол Е символымен белгіленеді.

Егер бас диагоналдан төмен орналасқан немесе жоғары орналасқан элементтері нөлге тең болса, онда квадратты матрица үшбұрышты матрица деп аталады.

Егер матрица бір тік (жатық) жолдан анықталса, онда ол матрица тік (жатық) жолды матрица деп аталады.

Бірдей ретті A мен B матрицалар тең деп аталады, егер олардың сәйкес элементтері тең болса.

Анықтама. 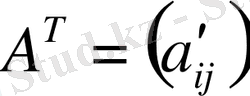матрица m*n ретті А матрицасының транспонирленген матрицасы деп аталады, егер 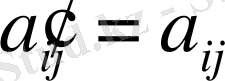теңдігі орындалса, және ол былай белгіленеді:

(3)

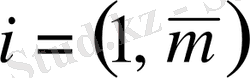
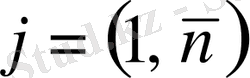
Осы анықтамадан, А-матрицасының жатық жолдарының элементтерін оның сәйкес тік жолдарының сәйкес элементтерімен орын алмастыру нәтижесінде берілген А матрицасының транспонирленген матрица n* m-ретті матрица екендігі шығады.

Берілген квадрат А матрицаның анықтауышы немесе детерминанты мына түрде белгіленеді

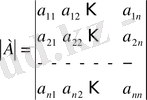Equation. 3 немесе det A= Equation. 3

Анықтама. Егер А матрицасының анықтауышы нөлге тең болмаса, яғни 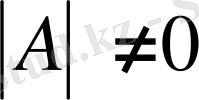онда А матрица ерекше емес матрица деп аталады, ал егер 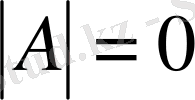болса, онда ол ерекше матрица деп аталады.

2. Матрицаларға қолданылатын амалдар.

Матрицаларға қосу, алу, көбейту және нақты санды матрицаға көбейту амалдары орындалады.

1. Матрицаларды қосу және азайту.

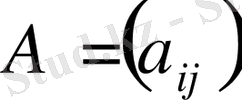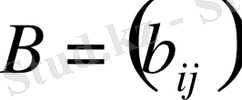Бірдей ретті мен матрицаларының қосындысы (айырмасы) деп сол ретті 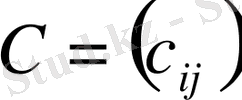матрицасын айтады: 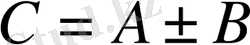және оның кез келген элементтері мына формуладан анықталады:

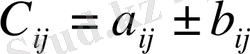
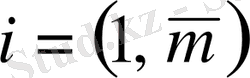
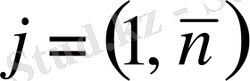
2. Матрицаларды нақты санға көбейту:

Кез келген А матрицаны нақты санына көбейту үшін матрицаның барлық элементтерін сол санға көбейту керек.

3. Матрицаларды көбейту.

Берілген m*n ретті А матрицаның n*k ретті В матрицаға көбейтіндісі деп, m*n ретті С матрицаны айтады:

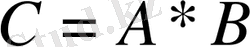
Ал оның кез келген элементтері 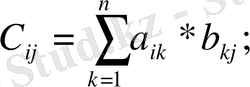(4)

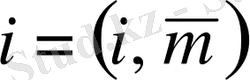
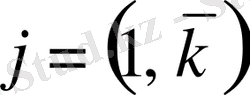
Осы анықтамадан А матрицаны В матрицаға көбейтуге болады, егер А матрицаның тік жолының саны В матрицасының жатық жолының санына тең болса, бұл жағдайда 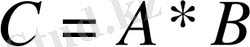матрицаның жатық жолының саны А матрицаның жатық жолының санына тең, ал оның тік жолының саны В матрицаның тік жолының санына тең.

Демек, егер А*В мен В*А көбейтінділері бар болғанымен де олар өзара тең емес, яғни 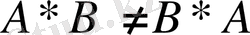. Жалпы жағдайда матрицалар көбейтінділеріне ауыстырымдылық қасиет орындалмайды. Сонымен (4) формуладан матрицалардың көбейтінділеріне мына қасиеттер орындалады (егер көбейтінділер бар болса) :

1) терімділік қасиет :

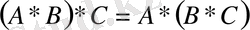
2 ) үлестірімділік қасиет :

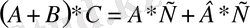
Тікелей көбейту арқылы А*Е=Е*А=А теңдігі орындалатындығына оңай көз жеткіземіз.

3. Анықтауыштың негізгі қасиеттері.

Анықтама. Реті n-ге тең анықтауыш деп (1) матрицаның жатық жолдары мен тік жолдарының әрқайсысынан бір-бірден алынған n элементтің көбейтіндісінен тұратын n! қосылғыштың алгебралық қосындысын айтады. n -ші ретті анықтауышты былай белгілейді:

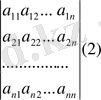
Δ =

Мұндағы 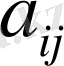- анықтауыштың элементтері болады. Бірінші индекс i жатық жолдың, екінші индекс j тік жолдың нөмірі. 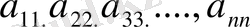элементтерінен тұратын диагонал басты диагонал деп, ал 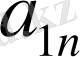, , 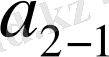, 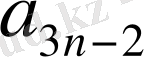. . . 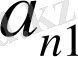элементтерінен тұратын диагонал көмекші (қосалқы) диагонал деп аталады.

n-ші ретті анықтауыштардың негізгі қасиеттері.

Анықтауыштарды есептеудің барлық тәсілдері сол анықтауыштың қасиеттеріне негізделген.

Жатық жолдары мен тік жолдарын ауыстырып қоюдан анықтауыштың шамасы өзгермейді.

Анықтауыштың кез келген екі жатық не екі тік жолдарын өзара ауыстырып қоюдан анықтауыштың тек таңбасы ғана өзгереді.

Егер анықтауыштың екі жатық не екі жолдары бірдей болса, онда ол анықтауыш нөльге тең.

Анықтауыштың бір жатық не тік жолының барлық элементтерін кез келген санына көбейту амалы анықтауышты осы санына көбейтумен бірдей.

Егер анықтауыштың кез келген жатық не тік жолының барлық элементтері нөльге тең болса, онда анықтауыш та нөльге тең.

Егер анықтауыштың екі жатық, не тік жолдарының сәйкес элементтері пропорционал болса, онда анықтауыш нөльге тең.

Егер анықтауыштың кез келген жатық не тік жолының барлық элементтері екі (не бірнеше) санның қосындысынан тұрса, онда ол анықтауыштың қосындысы етіп жазуға болады.

Анықтауыштың кез келген бір жатық жолының не тік жолының артық көбейткішін оның алдына шығаруға болады.

Анықтауыштың кез келген бір жатық жолының не тік жолының элементтерін бірдей санға көбейтіп, басқа жатық жолдың не тік жолдың сәйкес элементтеріне қосқаннан анықтауыш өзгермейді.

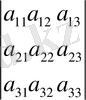= = (4)

Бұл формула Саррюс ережесі деп аталады («үшбұрыш» ережесі), оны үшінші ретті анықтауыштарды есептеу үшін қолданады. Схема түрінде былай көрсетуге болады:

4. Лаплас жіктеуі ( теоремасы) .

Реттері үлкен анықтауыштарды есептеу қиындыққа келтіреді, сондықтан оларды есептеу үшін анықтауыштардың қасиеттерін қолданады және Лапластың жіктеу теоремасын. Лапластың теоремасы берілген анықтауыштың ретін төмендетеді.

n -ші ретті анықтауыш берілсін делік:

Осы анықтауыштың 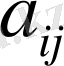элементінің миноры 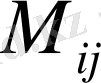деп, анықтауышының і жатық жолы мен j тік жолын сызып тастағаннан кейін қалатын (n-1) ретті анықтауышты айтады.

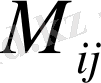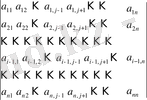= (5)

Берілген анықтауыштың 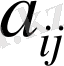элементінің алгебралық толықтауышы 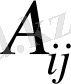деп, осы элементтің миноры 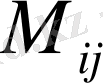мен 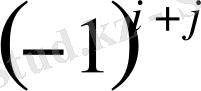өрнегінің көбейтіндісін айтады.

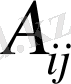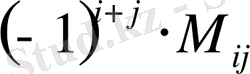= (6)

Лаплас теоремасы (Лапластың жіктеу теоремасы) . Анықтауыштың кез келген жатық (тік) жолдарының элементтерімен оның алгебралық толықтауыштарының көбейтінділерінің қосындысы осы анықтауыштың мәніне тең, яғни

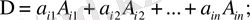
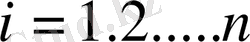(7)

Кез келген n-ші ретті анықтауыштарды есептеу үшін олардың тік немесе жатық элементтері бойынша жіктеу арқылы есептеуге болады. Бұл әдістің мақсаты - анықтауыштардың ретін төмендету. Лаплас теоремасы реті төртке тең немесе төрттен артық анықтауыштарды есептеуде қолданылады. (7) формуланы қолдану арқылы анықтауыштың ретін бірге төмендете отырып өзімізге белгілі болған үшінші немесе екінші ретті анықтауыштарға келтіруге болады және анықтауыштың қасиетін пайдаланып жіктейін деп отырған тік немесе жатық жолдын бір элементінен басқасы нөльге айналдыру арқылы есептеуді жеңілдетуге болады.

5. Кері матрица. Матрица рангісі.

... жалғасы

Сіз бұл жұмысты біздің қосымшамыз арқылы толығымен тегін көре аласыз.