Туынды және дифференциал: элементар функциялардың туындылары, геометриялық мағына және көп айнымалы функциялардағы толық дифференциал


Туынды және дифференциал.
1. Элементар функциялардың туындысы.
Айталық, Х аралығында у= ƒ (x) функциясы анықталсын. Бұл аралықтан х 0 нүктесін алып, оған ∆х өсімшесін берейік. Сонда, y=f(x) функциясы да өсімше қабылдайды:
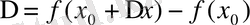 . Мұнда
. Мұнда
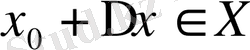 .
.
Анықтама. Егер ∆х нольге ұмтылғанда функция өсімшесі мен аргумент өсімшесі қатынасының шегі бар болса, онда бұл шек берілген функцияның х 0 нүктесіндегі туындысы деп аталады.
Сонымен, егер
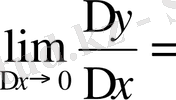
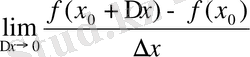
бар болса, оны берілген функцияның х 0 нүктсіндегі туындысы деп атайды.
Туындыны мынадай символдармен белгілейді:
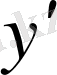 (игрек штрих),
(игрек штрих),
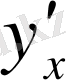 (игрек штрих
(игрек штрих
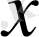 бойынша),
бойынша),
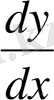 (де игрек де икстен),
(де игрек де икстен),
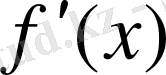 (эф штрих икстен) .
(эф штрих икстен) .
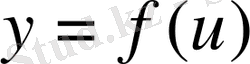 функциясы
функциясы
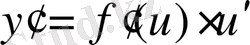

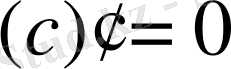
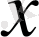
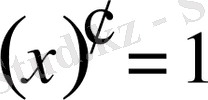

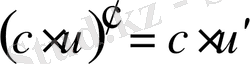

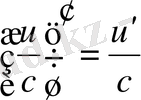

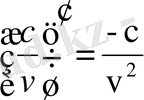
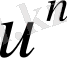
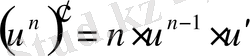
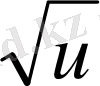
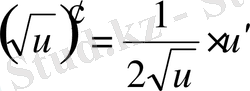
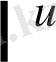
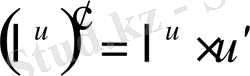
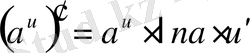
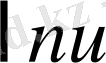
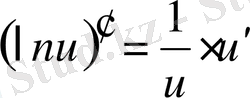
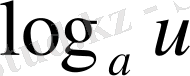
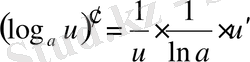

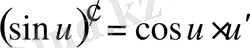
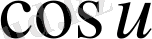
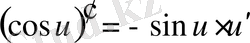
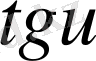
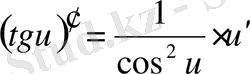
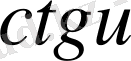
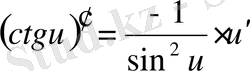
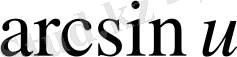
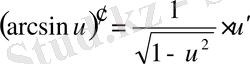

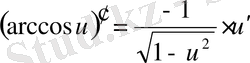
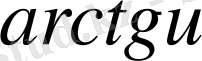
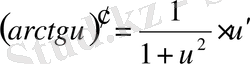
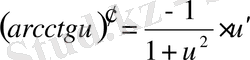
Егер осы формулалардағы u аралық айнымалы емес, тәуелсіз айнамалы десек, яғни u=x болса, онда әр формулада u′ -тін орнына бір саны жазылады, өйткені тәуелсіз айнымалы жағдайында u′ =x′=1 болады.
Мысалы,
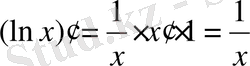
2. Күрделі, кері және анықталмаған функция туындысы.
Теорема
. Егер
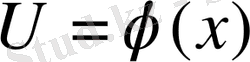 функциясының
х
нүктесінде, ал
y= ƒ(u)
функциясының сол
х
-ке сәйкес
функциясының
х
нүктесінде, ал
y= ƒ(u)
функциясының сол
х
-ке сәйкес
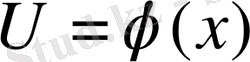 нүктесінде туындылары бар болса, онда сол
х
нүктесінде күрделі
нүктесінде туындылары бар болса, онда сол
х
нүктесінде күрделі
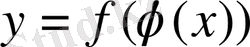 функциясының да туындысы бар болады және мынаған тең:
функциясының да туындысы бар болады және мынаған тең:
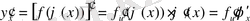
Теорема.
Егер
y=f(x)
функциясының
х
нүктесінде нөлге тең емес
y′=ƒ′(x) ≠0
туындысы бар болса, онда
х
-ке сәйкес
y
0
= ƒ(x
0
)
нүктесінде оған кері
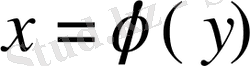 функциясының туындысы бар болады және
функциясының туындысы бар болады және
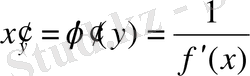 формуламен анықталады.
формуламен анықталады.
Негізгі элементар функциялар туындыларын кесте түрінде келтірейік. Бұл оларды пайдалануды жеңілдетеді. Осы мақсатпен кесте күрделі функциялар үшін жасалған, яғни мұнда u -аралық айнымалы.
3. Дифференциал түсінігі.
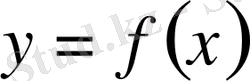 функцияның
функцияның
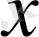 нүктесінде туындысы бар, яғни
нүктесінде туындысы бар, яғни
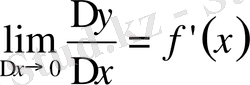 болсын.
болсын.
Ақырлы шегі бар функция мен ақырсыз кіші шаманың байланысын сипаттайтын теореманы қолданып, бұл теңдікті:
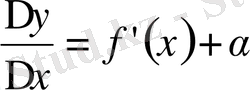 түрінде жазуға болады.
түрінде жазуға болады.
Мұндағы
 щамасы
щамасы
 -пен бірге нольге ұмтылатын оның ақырсыз кіші функциясы болады, яғни егер
-пен бірге нольге ұмтылатын оның ақырсыз кіші функциясы болады, яғни егер
 болса, онда
болса, онда
 . Енді теңдіктің екі жағын да
. Енді теңдіктің екі жағын да
 -ке көбейтсек,
-ке көбейтсек,
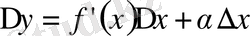 (1)
(1)
Анықтама.
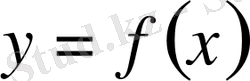 функциясының
функциясының
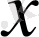 нүктесіндегі дифференциалы деп функцияның сол
нүктесіндегі дифференциалы деп функцияның сол
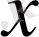 нүктесіндегі өсімшесінің басты бөлігін атайды және оны
нүктесіндегі өсімшесінің басты бөлігін атайды және оны
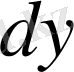 немесе
немесе
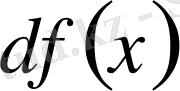 деп белгілейді.
деп белгілейді.
Сонымен,
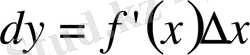 (2)
(2)
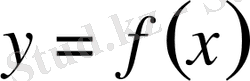 функциясының дифференциалы болады. Мысалы,
функциясының дифференциалы болады. Мысалы,
 функциясының дифференциалын табайық. Формула бойынша оның дифференциалы
функциясының дифференциалын табайық. Формула бойынша оның дифференциалы
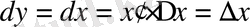 немесе
немесе
 , яғни тәуелсіз айнымалының дифференциалы оның өсімшесіне тең болады.
, яғни тәуелсіз айнымалының дифференциалы оның өсімшесіне тең болады.
(2) формуласын енді
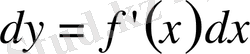 (3)
(3)
деп жазуға болады, яғни
функцияның дифференциалы
оның туындысы мен тәуелсіз айнымалы дифференциалының көбейтіндісіне тең болады. (3) теңдіктің екі жағын да
 -ке бөлсек,
-ке бөлсек,
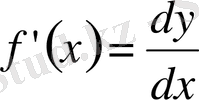
болады, яғни
функцияның
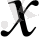 нүктесіндегі туындысы
оның сол нүктедегі дифференциалын тәуелсіз айнымалының дифференциалына бөлгенге тең болады.
нүктесіндегі туындысы
оның сол нүктедегі дифференциалын тәуелсіз айнымалының дифференциалына бөлгенге тең болады.
4. Геометриялық мағынасы.
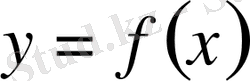 функциясының
функциясының
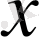 нүктесіндегі дифференциалының анықтамасынан
нүктесіндегі дифференциалының анықтамасынан
 өсімшесі мен
өсімшесі мен
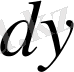 дифференциалының арасында
дифференциалының арасында
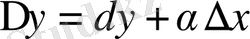 немесе
немесе
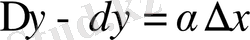 түріндегі байланыс бар болады, мұндағы
түріндегі байланыс бар болады, мұндағы
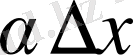 шамасы
шамасы
 -ке қарағанда жоғары ретті ақырсыз кіші шама, яғни
-ке қарағанда жоғары ретті ақырсыз кіші шама, яғни
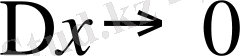 болғанда
болғанда
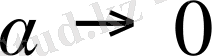 . Сондықтан жуықтап есептеулерде
. Сондықтан жуықтап есептеулерде
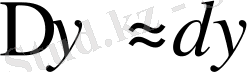 жуық теңдігін қолданады, немесе оны ашып, толық түрде былай жазады:
жуық теңдігін қолданады, немесе оны ашып, толық түрде былай жазады:
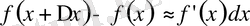
Бұдан,
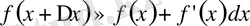 (4)
(4)
Бұл формула
 шамасы өте аз, ал
шамасы өте аз, ал
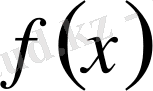 пен
пен
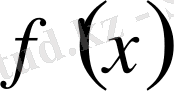 белгілі болғанда ғана
белгілі болғанда ғана
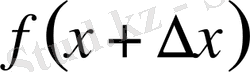 функциясының мәнін жуықтап табуға мүмкіндік береді.
функциясының мәнін жуықтап табуға мүмкіндік береді.
5. Көп айнымалылы функция. Дербес туындылар. Толық дифференциал.
Анықтама.
Реттелген
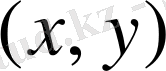 сандар жұбының
сандар жұбының
 жиыны берілсін. Егер әрбір
жиыны берілсін. Егер әрбір
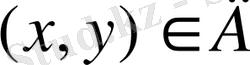 сандар жұбына қандай да бір
f
ережесі бойынша х шамасының анықталған бір мәні сәйкес келсе, онда
сандар жұбына қандай да бір
f
ережесі бойынша х шамасының анықталған бір мәні сәйкес келсе, онда
 жиынында анықталған екі айнымалды функция берілді дейді де оны
жиынында анықталған екі айнымалды функция берілді дейді де оны
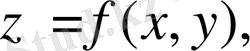 деп белгілейді
деп белгілейді
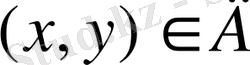 .
.
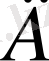 жиыны функцияның анықталу аймағы (облысы) деп аталады.
жиыны функцияның анықталу аймағы (облысы) деп аталады.
Дербес туындылар .
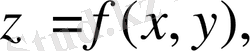 функциясының
функциясының
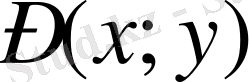 нүктесіндегі
нүктесіндегі
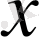 бойынша дербес туындысы деп,
бойынша дербес туындысы деп,
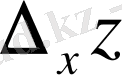 дербес өсімшесінің Δх өсімшесіне қатынасының
дербес өсімшесінің Δх өсімшесіне қатынасының
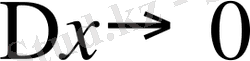 үмтылғандағы шегін (егер ол шек бар болса) айтады да
үмтылғандағы шегін (егер ол шек бар болса) айтады да
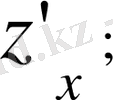
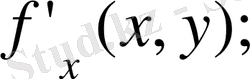
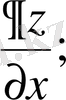
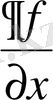 символдарының біреуімен белгілейді. Сонымен,
символдарының біреуімен белгілейді. Сонымен,
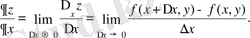
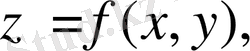 функциясының
функциясының
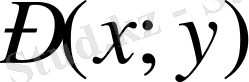 нүктесіндегі
нүктесіндегі
 бойынша дербес туындысы да дәл осылай анықталады және
бойынша дербес туындысы да дәл осылай анықталады және
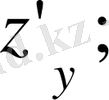
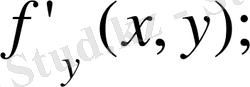
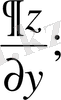
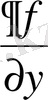 символдарының біреуімен белгіленеді
символдарының біреуімен белгіленеді
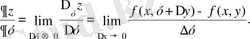
Функцияның толық дифференциалы.
Анықтама.
Егер
 функциясы (
x; y)
нүктесінде дифференциалданса, онда оның осы нүктедегі өсімшесінің сызықтық бас бөлігі
функциясы (
x; y)
нүктесінде дифференциалданса, онда оның осы нүктедегі өсімшесінің сызықтық бас бөлігі
 функциясының толық дифференциалы деп аталады да
функциясының толық дифференциалы деп аталады да
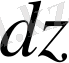 немесе
немесе
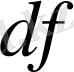 арқылы белгіленеді.
арқылы белгіленеді.
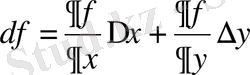
Мұндағы
 ,
,
 тәуелсіз айнымалдар өсімшелерін
тәуелсіз айнымалдар өсімшелерін
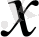 пен
пен
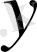 тәуелсіз айнымалдарының дифференциалдары деп атайды, және оларды
тәуелсіз айнымалдарының дифференциалдары деп атайды, және оларды
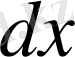 және
және
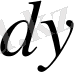 арқылы белгілейді. Онда толық дифференциал келесі түрге ие болады:
арқылы белгілейді. Онда толық дифференциал келесі түрге ие болады:
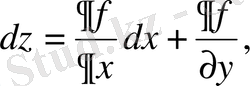 және де
және де

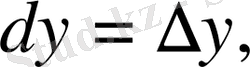

- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz