Алгебралық теңдеулер жүйелерін шешудің дәл және итерациялық әдістері


Қазақстан Республикасының Білім және ғылым министрлігі
КУРСТЫҚ ЖҰМЫС
Тақырыбы:
«Алгебралық теңдеулер жүйесі»
Орындаған:
Тексерген:
Орал, 2014ж.
Мазмұны
Кіріспе . . . 3
Негізгі бөлім
1. Алгебралық теңдеулер жүйесін «Гаусс» әдісімен шешу . . . 5
2. Алгебралық теңдеулер жүйесін «Квадрат түбірлер» әдісімен шешу . . . 12
3. Алгебралық теңдеулер жүйесін «Негізгі элементтер»
және «Халецкий» әдісімен шешу . . . 15
4. Алгебралық теңдеулер жүйесін «Итерация» әдісімен шешу . . . 20
5. Алгебралық теңдеулер жүйесін «Зейдел» әдісімен шешу . . . 24
6. Алгебралық теңдеулер жүйесін «Релаксация» әдісімен шешу . . . 27
Қолданылған әдебиеттер . . . 29
Кіріспе
Тақырыптың өзектілігі . Алгебралық теңдеулер жүйесін шешу әдістері сандық әдістер курсының негізгі бөлімдерінің бірі болып табылады. Ғылыми-техникалық есептеулер жұмыстарын жүргізу, сол сияқты инженерлік зерттеулер кезінде т. б. көптеген жағдайларда алгебралық теңдеулер жүйесін шешуге тура келеді. Сондықтан қолданбалы математика, информатика және математика мамандықтары бойынша студенттерді жоғарғы мектеп талаптарына сай дәрежеде дайындау- қазіргі заманның өзекті мәселелерінің бірі болып табылады.
Білім өркениеттіліктің әрі өлшемі, әрі тетігі болып табылатындықтан кез келген мемлекеттің рухани және әлеуметтік дәрежесі білім деңгейіне байланысты бағаланады.
Жан-жақты үйлесімді, өркениетті елдің ұрпағын тәрбиелеп шығу бүгінгі мектептің алдына қойылған мақсаттардың бірі. Бұл мақсат әрбір орта мектеп мұғалімінен бүгінгі заман талабына сай оқыту әдістемесін күннен күнге жетілдіре түсуін талап етеді. Осы талаптың орындалуы орта мектеп бағдарламасындағы әрбір пәннің әр тарауының әр тақырыбын оқушы санасына жететіндей етіп оқытқанда ғана орындалады. Олай болса, оқушыларды жеке тұлға етіп тәрбиелеуде математика пәнінің де алатын орны, салмағы зор.
Зерттеу жұмыстың мақсаты “сандық әдістер” курсының теңдеулер жүйесін шешу тақырыптары бойынша дәрістік, зертханалық сабақтарды жүргізуде қолданылатын әдістемелік құрал жасау. Пәнді жетік меңгеруде қазақ тілінде жазылған оқулық, әдістемелік нұсқаулардың аздығы белгілі бір дәрежеде қиындықтар тудыруда. Осындай қажеттілікті шешудің бір жолы - ол мемлекеттік тілде әдістемелік нұсқаулар құру болып табылады.
Зерттеу жұмысының міндеттері: Алгебралық теңдеулер жүйесін шешу әдістері туралы түсінік беру, алгебралық теңдеулер жүйесін шешеу тәсілдерін көрсету.
Теңдеулер жүйесін шешу әдістері негізінен екі топқа бөлінеді:
1 - топ - дәл әдістер тобы - мұнда теңдеулер жүйесін шешу алгоритмі ақырлы. Бұл топқа Гаусс әдісі, негізгі элементтер әдісі, квадрат түбірлер әдісі және т. б жатады.
2 - топ - итерациялық әдістер тобы, мұнда теңдеулер жүйесі берілген дәлдікпен, жинақты болатын шексіз процесстердің нәтижесінде шешіледі. Оларға итерация, Зейдель, релаксация және т. б әдістер жатады.
Есептеулер кезінде дөңгелектеу қолданылатындықтан, дәл әдістердің нәтижелері де жуық болады. Ал итерациялық процесстерде есептеулер қателіктеріне, әдіс қателігі де қосылады. Итерациялық үрдістің эффективтілігі алынған алғашқы жуықтауға және процесс жинақтылығының жылдамдығына байланысты болады.
Зерттеу жұмысының құрылымы : кіріспеден, теориялық, практикалық бөлімдерден, тапсырмалардан, қорытынды және әдебиеттер тізімінен тұрады.
Теориялық бөлімде дәл әдістер тобына жататын Гаусс, квадрат түбірлер, Халецкий, негізгі элементтер, итерациялық әдістері тобына жататын Зейдел, релаксация, қарапайым итерация әдістері жан - жақты қарастырылған.
Негізгі бөлім
1. Алгебралық теңдеулер жүйесін «Гаусс» әдісімен шешу
Анықтық үшін төрт белгісізі бар төрт теңдеуден тұратын жүйені қарастырайық.
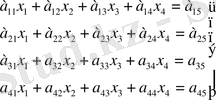 (1. 2. 1)
(1. 2. 1)
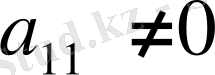 ,
,
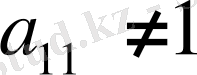 болсын.
болсын.
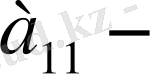 жетекші элемент деп аталады. (1. 2. 1) - жүйесінің бірінші теңдеуін
жетекші элемент деп аталады. (1. 2. 1) - жүйесінің бірінші теңдеуін
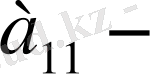 ге мүшелеп бөлеміз:
ге мүшелеп бөлеміз:
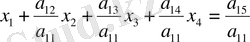
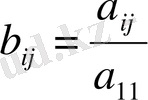
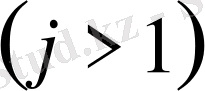 белгілеуін енгізсек:
белгілеуін енгізсек:
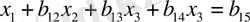 (1. 2. 2)
(1. 2. 2)
(1. 2. 2) - теңдеуін қолданып, (1. 2. 1) - жүйесінің
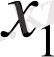 белгісізін алып тастауға болады. Ол үшін (1. 2. 2) - теңдеуді алдымен
белгісізін алып тастауға болады. Ол үшін (1. 2. 2) - теңдеуді алдымен
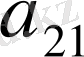 - ге, одан соң
- ге, одан соң
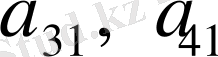 - ге көбейтіп, (1. 2. 1) жүйесінің 2 - ші, 3 - ші, 4 - ші теңдеулерінен шегеру керек.
- ге көбейтіп, (1. 2. 1) жүйесінің 2 - ші, 3 - ші, 4 - ші теңдеулерінен шегеру керек.
Нәтижесінде үш теңдеуден тұратын жүйе аламыз:
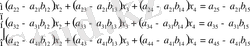
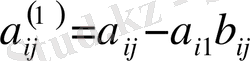
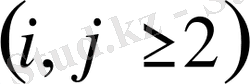 белгілеуі арқылы
белгілеуі арқылы
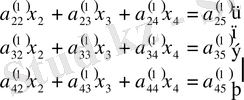 (1. 2. 1
/
)
(1. 2. 1
/
)
аламыз. Мұндағы
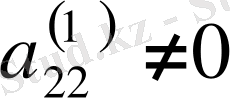 ,
,
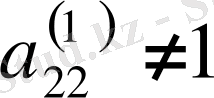 - жетекші элемент болсын.
- жетекші элемент болсын.
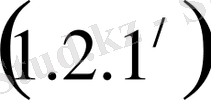 жүйесінің бірінші теңдеуін мүшелеп жетекші элементке бөлсек:
жүйесінің бірінші теңдеуін мүшелеп жетекші элементке бөлсек:
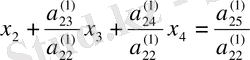
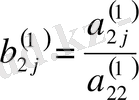
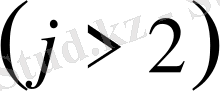 белгілеуін енгізсек:
белгілеуін енгізсек:
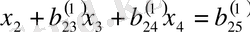 , (2. 2. 2
/
)
, (2. 2. 2
/
)
Енді (1. 2. 1
/
) жүйесінен
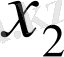 белгісізін жоғарыдағыдай жолмен алып тастаймыз, нәтижесінде екі белгісізі бар екі теңдеулер жүйесін аламыз:
белгісізін жоғарыдағыдай жолмен алып тастаймыз, нәтижесінде екі белгісізі бар екі теңдеулер жүйесін аламыз:
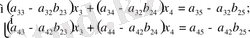
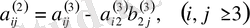
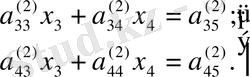 (1. 2. 1
//
)
(1. 2. 1
//
)
Мұнда
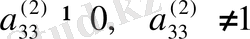 - жетекші элемент.
- жетекші элемент.
(1. 2. 1 // ) жүйесінің бірінші теңдеуін жетекші элементке мүшелеп бөлсек:
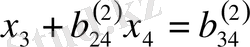 , (
, (
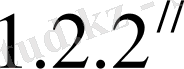 )
)
Енді (1. 2. 1
//
) жүйесінен
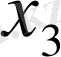 белгісізін алып тастаймыз:
белгісізін алып тастаймыз:
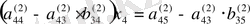
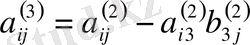 ,
,
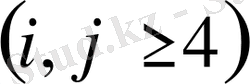
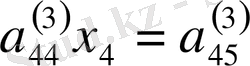 .
.
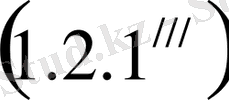
Бұдан
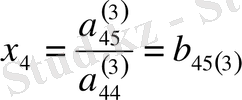
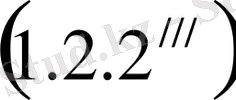
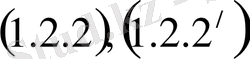 ,
,
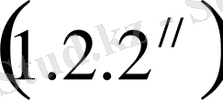 және
және
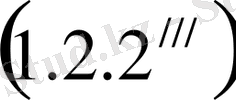 теңдеулерін жинақтап жазсақ, белгісіздерді анықтауға мүмкіндік беретін үшбұрышты жүйе аламыз:
теңдеулерін жинақтап жазсақ, белгісіздерді анықтауға мүмкіндік беретін үшбұрышты жүйе аламыз:
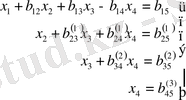 (1. 2. 3)
(1. 2. 3)
Гаусс әдісін қолданып теңдеулер жүйесін шешу үшін қажетті және жеткілікті шарты - ол жетекші элеметтердің барлығының нөлге тең болмауы болып табылады.
Үшбұрышты матрицаның (1. 2. 3) коэффициенттерін анықтау үрдісі тура жүріс, ал (1. 2. 1) жүйесінің белгісіздерін анықтау кері жүріс деп аталады.
Практикада Гаусс әдісімен теңдеулер жүйесін шешуді жеңілдету үшін арнайы есептеу кестелері қолданылады.
Тура жүріс кестенің А бөліміне жүйенің коэффициенттерін және бос мүшелерді жазудан басталады. А бөлімінің ең соңғы жолы бірінші жолды мүшелеп
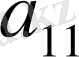 - ге бөлудің нәтижелерінен тұрады. А
1
бөлімінің кез келген элементі
- ге бөлудің нәтижелерінен тұрады. А
1
бөлімінің кез келген элементі
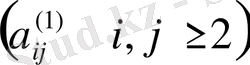 А бөлімінің сәйкесінше
А бөлімінің сәйкесінше
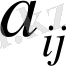 элементтерінен бірінші тік жол мен соңғы жатық жолдың сәйкес элементерінің көбейтіндісін шегерумен анықталады.
элементтерінен бірінші тік жол мен соңғы жатық жолдың сәйкес элементерінің көбейтіндісін шегерумен анықталады.
Ал А
1
бөлімінің соңғы жатық жолы бірінші жолды
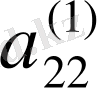 - жетекші элементке бөлгеннен пайда болады.
- жетекші элементке бөлгеннен пайда болады.
Осындай жолмен қалған А 2 , А 3 бөлімдері құрылады.
Ал, кері жүрісте А
i
бөлімдерінің (белгіленген жатық жолдары) 1 саны бар жатық жолдары қолданылады. Бұлардан алдымен
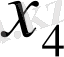 Equation. 3, одан соң
Equation. 3, одан соң
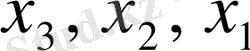 Equation. 3 белгісіздері анықталады. Олардың мәндері ең соңғы бөлімге жазылады.
Equation. 3 белгісіздері анықталады. Олардың мәндері ең соңғы бөлімге жазылады.
Есептеулерді бақылау үшін «бақылау қосындылары» қолданылады.
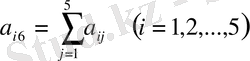 (1. 2. 4)
(1. 2. 4)
Бұл қосындылар сәйкес жатық жолдағы коэффициенттер мен бос мүшелердің қосындысын анықтайды.
Егер (1. 1. 1) жүйесінде бос мүшелер ретінде
 коэффициентін алсақ, онда түрлендірілген алгебралық жүйедегі:
коэффициентін алсақ, онда түрлендірілген алгебралық жүйедегі:
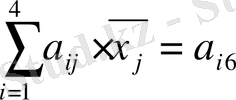
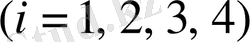 (1. 2. 5)
(1. 2. 5)
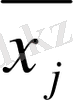 белгісіздері алғашқы жүйенің белгісіздері
белгісіздері алғашқы жүйенің белгісіздері
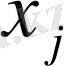 мен төмендегідей қатынаста болды:
мен төмендегідей қатынаста болды:
 (1. 2. 6)
(1. 2. 6)
Шындығында да (1. 2. 6) формуласын (1. 2. 5) теңдеуіне қойып, (1. 2. 1) және (1. 2. 4) формуласын қолдансақ, тепе - теңдік аламыз:
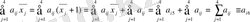 .
.
Практикада әрбір жолдағы есептеуді бақылау үшін, кестеде тағы бір тік жол қолданылады. Ол жол «жолдық бақылау» деп аталады. Ол тік жолдың элементтері әрбір бөлімнің элементтері қалай анықталса, сондай әдіспен анықталады. Нәтижелері S бағанына жазылады.
Егер ағымдық жолда ешқандай қателер пайда болмаса, онда осы жолдағы
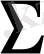 мен S бағандарының элементтері бірдей болады (белгілі бір дәлдікке дейін) .
мен S бағандарының элементтері бірдей болады (белгілі бір дәлдікке дейін) .
Кестеде үш теңдеулердің жүйесін қарастырайық
Кесте 1 Гаусс сызбасы
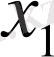
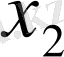
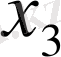
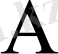






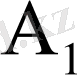
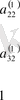
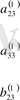
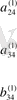
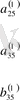
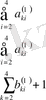




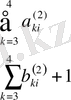
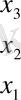
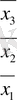
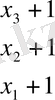
1. 3 Гаусс әдісінің көмегімен анықтауышты есептеу
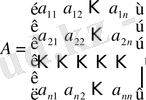 (1. 3. 1)
(1. 3. 1)
алгебралық теңдеулер жүйесінің коэффициенттерінің анықтауышы.
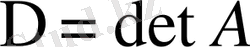 (1. 32)
(1. 32)
Алгебралық теңдеулер жүйесін
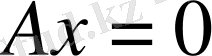 (1. 3. 3)
(1. 3. 3)
қарастырайық. (1. 3. 3) жүйесін Гаусс әдісімен үшбұрышты матрицасына түрлендіреміз, яғни
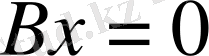 (1. 3. 3)
(1. 3. 3)
мұндағы В:

В матрицасының элементтері А матрицасының элементтерінен және
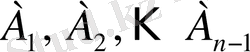 көмекші матрицаларынан төмендегідей элементарлық түрлендірулердің көмегімен анықталады:
көмекші матрицаларынан төмендегідей элементарлық түрлендірулердің көмегімен анықталады:
1)
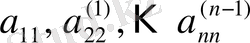 жетекші элементтерге бөлу. Мұнда жетекші элементтер нөлге тең емес.
жетекші элементтерге бөлу. Мұнда жетекші элементтер нөлге тең емес.
2) А матрицасының сәйкес элементтерінен тік жол мен жатық жол элементтерінің көбейтіндісі игеріледі.
Мұндай операциялар нәтижесінде:
- А матрицасының анықтауышы да сәйкес жетекші элементтерге бөлінеді.
б) екінші операцияда А анықтауышы өзгермейді.
Олай болса,
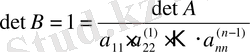 ; бұдан
; бұдан
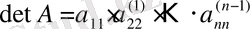 (1. 3. 4)
(1. 3. 4)
Сонымен, жүйенің анықтауышы жетекші элементтердің көбейтіндісіне тең. Ал жетекші элементтерді анықтау үшін арнайы жоғарыда қарастырылған Гаусс кестесін қолдану тиімді.
Егер белгілі бір қадамдарда
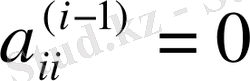 немесе нөлге жуық сандар болса, онда жатық және тік жолдарын ауыстыру керек.
немесе нөлге жуық сандар болса, онда жатық және тік жолдарын ауыстыру керек.
Мысал 1. 3. 1: Төмендегі анықтауыштың мәнін есептеңіз:

Анықтауыштың мәнін есептеу үшін Гаусс әдісін қолданамыз.
Кесте 3 Анықтауышты есептеу кестесі
Кесте 3 жалғасы
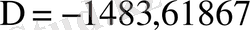 - анықтауыштың мәні.
- анықтауыштың мәні.
Гаусс әдісімен кері матрицаны есептеу
Бізге айрықша емес матрица берілсін
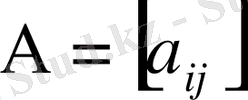
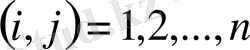 (1. 4. 1)
(1. 4. 1)
Анықтама. Егер
 болса, онда А матрицасы айрықша емес матрица деп аталады.
болса, онда А матрицасы айрықша емес матрица деп аталады.
Оның кері матрицасы
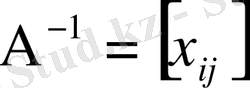 анықтау үшін алгебра курсынан белгілі негізгі қатынасты қолданамыз, яғни:
анықтау үшін алгебра курсынан белгілі негізгі қатынасты қолданамыз, яғни:
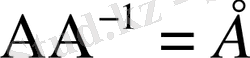 , мұндағы Е - бірлік матрица.
, мұндағы Е - бірлік матрица.
А және А
-1
матрицаларын көбейтіп,
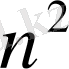 белгісіздерін анықтауға мүмкіндік беретін n теңдеулер жүйесін аламыз.
белгісіздерін анықтауға мүмкіндік беретін n теңдеулер жүйесін аламыз.
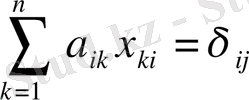
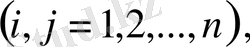
мұндағы
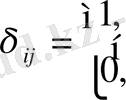
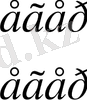
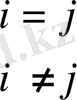 .
.
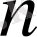 жүйелердің барлығының матрицасы бірдей, ол берлген теңдеулер жүйесінің коэффициенттерінің матрицасы, яғни (1. 4. 1) . Бұл жүйелердің әрқайсысына Гаусс әдісін қолданып, бір уақытта шешуге болады.
жүйелердің барлығының матрицасы бірдей, ол берлген теңдеулер жүйесінің коэффициенттерінің матрицасы, яғни (1. 4. 1) . Бұл жүйелердің әрқайсысына Гаусс әдісін қолданып, бір уақытта шешуге болады.
Практикада арнайы кестелер қолданылады, мұнда есептеулер бақылау қосындылары арқылы тексеріліп отырылады.
Мысал 2. 4. 1: Берілген матрица үшін
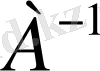 кері матрицасын табыңдар:
кері матрицасын табыңдар:
 .
.
Кесте 4 Кері матрицаны анықтау кестесі
- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz